adsense
Giải bài tập bài 2: Các phép tính với số hữu tỉ (Toán 7 Chân trời)
Giải bài 1 trang 15 SGK Toán 7 Chân trời sáng tạo tập 1
Tính:
(a)frac{2}{{15}} + left( {frac{{ – 5}}{{24}}} right))
b) (left( {frac{{ – 5}}{9}} right) – left( { – frac{7}{{27}}} right);)
c)(left( { – frac{7}{{12}}} right) + 0,75)
d)(left( {frac{{ – 5}}{9}} right) – 1,25)
e)(0,34.frac{{ – 5}}{{17}})
g) (frac{4}{9}:left( { – frac{8}{{15}}} right);)
h)(left( {1frac{2}{3}} right):left( {2frac{1}{2}} right))
i) (frac{2}{5}.left( { – 1.25} right))
k) (left( {frac{{ – 3}}{5}} right).left( {frac{{15}}{{ – 7}}} right).3frac{1}{9})
Phương pháp giải
– Đưa các số về phân số
– Thực hiện quy tắc cộng, trừ, nhân, chia số hữu tỉ.
Lời giải chi tiết
(a)frac{2}{{15}} + left( {frac{{ – 5}}{{24}}} right) = frac{{16}}{{120}} + left( {frac{{ – 25}}{{120}}} right) = frac{{ – 9}}{{120}} = frac{{ – 3}}{{40}})
b) (left( {frac{{ – 5}}{9}} right) – left( { – frac{7}{{27}}} right) = left( {frac{{ – 15}}{{27}}} right) + frac{7}{{27}} = frac{{ – 8}}{{27}})
c)(left( { – frac{7}{{12}}} right) + 0,75 = left( { – frac{7}{{12}}} right) + frac{3}{4} = left( { – frac{7}{{12}}} right) + frac{9}{{12}} = frac{2}{{12}} = frac{1}{6})
d)(left( {frac{{ – 5}}{9}} right) – 1,25 = left( {frac{{ – 5}}{9}} right) – frac{5}{4} = left( {frac{{ – 20}}{{36}}} right) – frac{{45}}{{36}} = frac{{ – 65}}{{36}})
e)(0,34.frac{{ – 5}}{{17}} = frac{{17}}{{50}}.frac{{ – 5}}{{17}} = frac{{ – 1}}{{10}})
g) (frac{4}{9}:left( { – frac{8}{{15}}} right) = frac{4}{9}.left( { – frac{{15}}{8}} right) = frac{{ – 5}}{6})
h)(left( {1frac{2}{3}} right):left( {2frac{1}{2}} right) = frac{5}{3}:frac{5}{2} = frac{5}{3}.frac{2}{5} = frac{2}{3})
i) (frac{2}{5}.left( { – 1.25} right) = frac{2}{5}.frac{{ – 5}}{4} = frac{{ – 1}}{2})
k) (left( {frac{{ – 3}}{5}} right).left( {frac{{15}}{{ – 7}}} right).3frac{1}{9} = left( {frac{{ – 3}}{5}} right).left( {frac{{15}}{{ – 7}}} right).frac{{28}}{9} = frac{{ – 3.3.5.7.4}}{{5.left( { – 7} right).3.3}} = 4)
Giải bài 2 trang 15 SGK Toán 7 Chân trời sáng tạo tập 1
Tính:
a)(0,75 – frac{5}{6} + 1frac{1}{2};)
b)(frac{3}{7} + frac{4}{{15}} + left( {frac{{ – 8}}{{21}}} right) + left( { – 0,4} right);)
c)(0,625 + left( {frac{{ – 2}}{7}} right) + frac{3}{8} + left( {frac{{ – 5}}{7}} right) + 1frac{2}{3})
d)(left( { – 3} right).left( {frac{{ – 38}}{{21}}} right).left( {frac{{ – 7}}{6}} right).left( { – frac{3}{{19}}} right);)
e) (left( {frac{{11}}{{18}}:frac{{22}}{9}} right).frac{8}{5};)
g)(left[ {left( {frac{{ – 4}}{5}} right).frac{5}{8}} right]:left( {frac{{ – 25}}{{12}}} right))
Phương pháp giải
– Đưa các số thập phân về dạng phân số (nếu có)
– Thực hiện phép tính theo thứ tự nhân, chia trước, cộng trừ sau.
Lời giải chi tiết
a)
(begin{array}{l}0,75 – frac{5}{6} + 1frac{1}{2} = frac{3}{4} – frac{5}{6} + frac{3}{2}\ = frac{9}{{12}} – frac{{10}}{{12}} + frac{{18}}{{12}} = frac{{17}}{{12}}end{array})
b)
(begin{array}{l}frac{3}{7} + frac{4}{{15}} + left( {frac{{ – 8}}{{21}}} right) + left( { – 0,4} right) = frac{3}{7} + frac{4}{{15}} – frac{8}{{21}} – frac{2}{5}\ = left( {frac{3}{7} – frac{8}{{21}}} right) + left( {frac{4}{{15}} – frac{2}{5}} right)\ = left( {frac{9}{{21}} – frac{8}{{21}}} right) + left( {frac{4}{{15}} – frac{6}{{15}}} right)\ = frac{1}{{21}} + left( {frac{{ – 2}}{{15}}} right)\ = frac{5}{{105}} – frac{{14}}{{105}}\ = frac{{ – 9}}{{105}} = frac{{ – 3}}{{35}}end{array})
c)
(begin{array}{l}0,625 + left( {frac{{ – 2}}{7}} right) + frac{3}{8} + left( {frac{{ – 5}}{7}} right) + 1frac{2}{3}\ = frac{5}{8} + left( {frac{{ – 2}}{7}} right) + frac{3}{8} – frac{5}{7} + frac{5}{3}\ = left( {frac{5}{8} + frac{3}{8}} right) + left( {frac{{ – 2}}{7} – frac{5}{7}} right) + frac{5}{3}\ = 1 – 1 + frac{5}{3} = frac{5}{3}end{array})
d)
(begin{array}{l}left( { – 3} right).left( {frac{{ – 38}}{{21}}} right).left( {frac{{ – 7}}{6}} right).left( { – frac{3}{{19}}} right)\ = frac{{ – 3.left( { – 38} right).left( { – 7} right).left( { – 3} right)}}{{21.6.19}}\ = frac{{3.38.7.3}}{{21.6.19}}\ = frac{{3.2.19.7.3}}{{3.7.3.2.19}}\ = 1end{array})
e)
(begin{array}{l}left( {frac{{11}}{{18}}:frac{{22}}{9}} right).frac{8}{5} = left( {frac{{11}}{{18}}.frac{9}{{22}}} right).frac{8}{5}\ = frac{{11.9.4.2}}{{9.2.2.11.5}} = frac{2}{5}end{array})
g)
(left[ {left( {frac{{ – 4}}{5}} right).frac{5}{8}} right]:left( {frac{{ – 25}}{{12}}} right) = frac{{ – 20}}{{40}}:left( {frac{{ – 25}}{{12}}} right)\ = frac{{ – 1}}{2}.frac{{ – 12}}{{25}} = frac{6}{{25}})
Giải bài 3 trang 15 SGK Toán 7 Chân trời sáng tạo tập 1
Thay dấu ? bằng dấu (>,<,=) thích hợp.
(begin{array}{l}
a)left( {frac{{ – 5}}{8}} right) + left( {frac{3}{{ – 8}}} right)? – 1;\
b)left( {frac{{ – 13}}{{22}}} right) + left( {frac{{ – 5}}{{22}}} right)?frac{{ – 8}}{{11}};\
c)frac{1}{6} + left( {frac{{ – 3}}{4}} right)?frac{1}{{14}} + left( {frac{{ – 4}}{7}} right).
end{array})
Phương pháp giải
– Thực hiện phép tính rồi so sánh
– Thay dấu “?” bởi dấu (>,<,=)
Lời giải chi tiết
a) (left( {frac{{ – 5}}{8}} right) + left( {frac{3}{{ – 8}}} right) = left( {frac{{ – 5}}{8}} right) + left( {frac{{ – 3}}{8}} right) = – 1)
Vậy dấu cần điền là “=”.
b) (left( {frac{{ – 13}}{{22}}} right) + left( {frac{{ – 5}}{{22}}} right) = frac{{ – 18}}{{22}} = frac{{ – 9}}{{11}} < frac{{ – 8}}{{11}}).
Vậy dấu cần điền là “<”.
c) (frac{1}{6} + left( {frac{{ – 3}}{4}} right) = frac{2}{{12}} + left( {frac{{ – 9}}{{12}}} right) = frac{{ – 7}}{{12}})
(frac{1}{{14}} + left( {frac{{ – 4}}{7}} right) = frac{1}{{14}} + left( {frac{{ – 8}}{{14}}} right) = frac{{ – 7}}{{14}})
Mà (frac{{ – 7}}{{12}} < frac{{ – 7}}{{14}})
Vậy dấu cần điền là “<”.
Giải bài 4 trang 15 SGK Toán 7 Chân trời sáng tạo tập 1
Tính:
a)(frac{3}{7}.left( { – frac{1}{9}} right) + frac{3}{7}.left( { – frac{2}{3}} right);)
b)(left( {frac{{ – 7}}{{13}}} right).frac{5}{{12}} + left( {frac{{ – 7}}{{13}}} right).frac{7}{{12}} + left( {frac{{ – 6}}{{13}}} right);)
c)(left[ {left( {frac{{ – 2}}{3} + frac{3}{7}} right)} right]:frac{5}{9} + left( {frac{4}{7} – frac{1}{3}} right):frac{5}{9})
d)(frac{5}{9}:left( {frac{1}{{11}} – frac{5}{{22}}} right) + frac{5}{9}:left( {frac{1}{{15}} – frac{2}{3}} right);)
e) (frac{3}{5} + frac{3}{{11}} – left( {frac{{ – 3}}{7}} right) + left( {frac{{ – 2}}{{97}}} right) – frac{1}{{35}} – frac{3}{4} + left( {frac{{ – 23}}{{44}}} right))
Phương pháp giải
– Áp dụng tính chất phân phối của phép nhân với phép cộng: a.c+b.c=(a+b).c
– Áp dụng tính chất giao hoán của phép cộng
Lời giải chi tiết
a)
(begin{array}{l}frac{3}{7}.left( { – frac{1}{9}} right) + frac{3}{7}.left( { – frac{2}{3}} right)\ = frac{3}{7}.left( { – frac{1}{9} + frac{-2}{3}} right)\ = frac{3}{7}.left( { – frac{1}{9} – frac{6}{9}} right)\ = frac{3}{7}.frac{{ – 7}}{9} = frac{{ – 1}}{3}end{array})
b)
(begin{array}{l}left( {frac{{ – 7}}{{13}}} right).frac{5}{{12}} + left( {frac{{ – 7}}{{13}}} right).frac{7}{{12}} + left( {frac{{ – 6}}{{13}}} right)\ = frac{{ – 7}}{{13}}.left( {frac{5}{{12}} + frac{7}{{12}}} right) + left( {frac{{ – 6}}{{13}}} right)\ = frac{{ – 7}}{{13}}.1 + left( {frac{{ – 6}}{{13}}} right)\ = frac{{ – 7}}{{13}} + left( {frac{{ – 6}}{{13}}} right)\ = frac{{ – 13}}{{13}}\ = -1end{array})
c)
(begin{array}{l}left[ {left( {frac{{ – 2}}{3} + frac{3}{7}} right)} right]:frac{5}{9} + left( {frac{4}{7} – frac{1}{3}} right):frac{5}{9}\ = left[ {left( {frac{{ – 2}}{3} + frac{3}{7}} right)} right].frac{9}{5} + left( {frac{4}{7} – frac{1}{3}} right).frac{9}{5}\ = left( {frac{{ – 2}}{3} + frac{3}{7} + frac{4}{7} – frac{1}{3}} right).frac{9}{5}\ = left[ {left( {frac{{ – 2}}{3} – frac{1}{3}} right) + left( {frac{3}{7} + frac{4}{7}} right)} right].frac{9}{5}\ = left( { – 1 + 1} right).frac{9}{5}\ = 0.frac{9}{5} = 0end{array})
d)
(begin{array}{l}frac{5}{9}:left( {frac{1}{{11}} – frac{5}{{22}}} right) + frac{5}{9}:left( {frac{1}{{15}} – frac{2}{3}} right)\ = frac{5}{9}:left( {frac{2}{{22}} – frac{5}{{22}}} right) + frac{5}{9}:left( {frac{1}{{15}} – frac{{10}}{{15}}} right)\ = frac{5}{9}:frac{{ – 3}}{{22}} + frac{5}{9}:frac{{ – 9}}{15}\= frac{5}{9}:frac{{ – 3}}{{22}} + frac{5}{9}:frac{{ – 3}}{5}\ = frac{5}{9}.frac{{ – 22}}{3} + frac{5}{9}.frac{{ – 5}}{3}\ = frac{5}{9}.left( {frac{{ – 22}}{3} – frac{5}{3}} right)\ = frac{5}{9}.frac{-27}{3}= frac{5}{9}.left( { – 9} right) = – 5end{array})
e)
(begin{array}{l}frac{3}{5} + frac{3}{{11}} – left( {frac{{ – 3}}{7}} right) + left( {frac{{ – 2}}{{97}}} right) – frac{1}{{35}} – frac{3}{4} + left( {frac{{ – 23}}{{44}}} right)\ = frac{3}{5} + frac{3}{{11}} + frac{3}{7} – frac{2}{{97}} – frac{1}{{35}} – frac{3}{4} – frac{{23}}{{44}}\ = left( {frac{3}{5} + frac{3}{7} – frac{1}{{35}}} right) + left( {frac{3}{{11}} – frac{3}{4} – frac{{23}}{{44}}} right) – frac{2}{{97}}\ = left( {frac{{21}}{{35}} + frac{{15}}{{35}} – frac{1}{{35}}} right) + left( {frac{{12}}{{44}} – frac{{33}}{{44}} – frac{{23}}{{44}}} right) – frac{2}{{97}}\ = 1 + left( { – 1} right) – frac{2}{{97}}\ = – frac{2}{{97}}end{array})
Giải bài 5 trang 15 SGK Toán 7 Chân trời sáng tạo tập 1
Tìm x, biết:
a) (x.frac{{14}}{{27}} = frac{{ – 7}}{9})
b) (left( {frac{{ – 5}}{9}} right):x = frac{2}{3};)
c) (frac{2}{5}:x = frac{1}{{16}}:0,125)
d) ( – frac{5}{{12}}x = frac{2}{3} – frac{1}{2})
Phương pháp giải
– Muốn tìm thừa số chưa biết, ta lấy tích chia cho thừa số còn lại
– Muốn tìm số chia, ta lấy số bị chia chia cho thương
Lời giải chi tiết
a)
(begin{array}{l}x.frac{{14}}{{27}} = frac{{ – 7}}{9}\x = frac{{ – 7}}{9}:frac{{14}}{{27}}\x = frac{{ – 7}}{9}.frac{{27}}{{14}}\x = frac{{ – 3}}{2}end{array})
Vậy (x = frac{{ – 3}}{2}).
b)
(begin{array}{l}left( {frac{{ – 5}}{9}} right):x = frac{2}{3}\x = left( {frac{{ – 5}}{9}} right):frac{2}{3}\x = left( {frac{{ – 5}}{9}} right).frac{3}{2}\x = frac{{ – 5}}{6}end{array})
Vậy (x = frac{{ – 5}}{6}).
adsense
c)
(begin{array}{l}frac{2}{5}:x = frac{1}{{16}}:0,125\frac{2}{5}:x = frac{1}{{16}}:frac{1}{8}\frac{2}{5}:x = frac{1}{{16}}.8\frac{2}{5}:x = frac{1}{2}\x = frac{2}{5}:frac{1}{2}\x = frac{2}{5}.2\x = frac{4}{5}end{array})
Vậy (x = frac{4}{5})
d)
(begin{array}{l} – frac{5}{{12}}x = frac{2}{3} – frac{1}{2}\ – frac{5}{{12}}x = frac{4}{6} – frac{3}{6}\ – frac{5}{{12}}x = frac{1}{6}\x = frac{1}{6}:left( { – frac{5}{{12}}} right)\x = frac{1}{6}.frac{{ – 12}}{5}\x = frac{{ – 2}}{5}end{array})
Vậy (x = frac{{ – 2}}{5}).
Chú ý: Khi trình bày lời giải bài tìm x, sau khi tính xong, ta phải kết luận.
Giải bài 6 trang 16 SGK Toán 7 Chân trời sáng tạo tập 1
Hai đoạn ống nước có chiều dài lần lượt là 0,8 m và 1,35 m. Người ta nối hai đầu ống để tạo thành một ống nước mới. Chiều dài của phần nối chung là (frac{2}{{25}})m. Hỏi đoạn ống nước mới dài bao nhiêu mét?
Phương pháp giải
Độ dài đoạn ống nước mới = Tổng chiều dài hai đoạn ống nước – chiều dài phần nối chung.
Lời giải chi tiết
Độ dài đoạn ống nước mới là:
(0,8 + 1,35 – frac{2}{{25}} = 2,15 – 0,08 = 2,07)(mét)
Vậy độ dài ống nước mới là: 2,07 m
Giải bài 7 trang 16 SGK Toán 7 Chân trời sáng tạo tập 1
Một nhà máy trong tuần thứ nhất đã thực hiện được (frac{4}{{15}}) kế hoạch tháng, trong tuần thứ hai thực hiện được (frac{7}{{30}}) kế hoạch, trong tuần thứ ba thực hiện được (frac{3}{{10}}) kế hoạch. Để hoàn thành kế hoạch của tháng thì trong tuần cuối nhà máy phải thực hiện bao nhiêu phần kế hoạch?
Phương pháp giải
– Tính tổng số phần công việc sau ba tuần nhà máy đã thực hiện được
– Lượng công việc tuần cuối nhà máy cần phải thực hiện = 1- tổng số phần công việc sau ba tuần nhà máy đã thực hiện được.
Lời giải chi tiết
Tổng số phần công việc sau ba tuần nhà máy đã thực hiện được là:
(frac{4}{{15}})+(frac{7}{{30}})+(frac{3}{{10}})=(frac{4}{5})(công việc)
Lượng công việc tuần cuối nhà máy cần thực hiện là:
(1 – frac{4}{5} = frac{1}{5}) (công việc)
Vậy tuần cuối nhà máy cần thực hiện (frac{1}{5}) công việc.
Chú ý:
Coi tổng số phần công việc cần hoàn thành là 1 công việc
Giải bài 8 trang 16 SGK Toán 7 Chân trời sáng tạo tập 1
Vào tháng 6, giá niêm yết một chiếc ti vi 42 inch tại một siêu thị điện máy là 8 000 000 đồng. Đến tháng 9, siêu thị giảm giá 5% cho mỗi chiếc ti vi. Sang tháng 10, siêu thị lại giảm giá thêm một lần nữa, lúc này giá một chiếc ti vi 42 inch chỉ còn 6 840 000 đồng. Hỏi tháng 10, siêu thị đã giảm giá bao nhiêu phần trăm cho một chiếc ti vi so với tháng 9?
Phương pháp giải
– Tính giá chiếc tivi trong tháng 9.
– Tính số tiền chiếc tivi sau khi được giảm giá trong tháng 10
– Tính số phần trăm giá tiền sau khi siêu thị đã giảm giá trong tháng 10 so với tháng 9
Lời giải chi tiết
Trong tháng giá chiếc ti vi còn: 100% – 5%=95% so với giá niêm yết.
Giá chiếc tivi trong tháng 9 là:
(8,000,000.frac{{95}}{{100}} = 7,600,000)(đồng)
Số tiền siêu thị đã giảm giá trong tháng 10 là:
7 600 000- 6 840 000 = 760 000 (đồng)
Tháng 10, siêu thị đã giảm giá số phần trăm cho một chiếc ti vi so với tháng 9 là:
760 000 : 7 600 000 .100 = 10%
Vậy trong tháng 10 siêu thị đã giảm giá 10% so với tháng 9.
Giải bài 9 trang 16 SGK Toán 7 Chân trời sáng tạo tập 1
Một cửa hàng sách có chương trình khuyến mãi như sau: Khách hàng có thẻ thành viên sẽ được giảm 10% tổng số tiền của hoá đơn. Bạn Lan có thẻ thành viên và bạn mua 3 quyển sách, mỗi quyển đều có giá 120 000 đồng. Bạn đưa cho cô thu ngân 350 000 đồng. Hỏi bạn Lan được trả lại bao nhiêu tiền?
Phương pháp giải
– Tính giá gốc 3 quyển sách
– Tính giá 3 quyển sách sau khi được giảm giá
– Tính số tiền Lan được trả lại khi đưa cho cô thu ngân 350 000 đồng.
Lời giải chi tiết
Giá gốc 3 quyển sách là:
3.120 000 = 360 000 (đồng)
Sau khi được giảm giá 10% thì giá 3 quyển sách bằng 90% giá ban đầu.
Giá 3 quyển sách sau khi được giảm giá là:
360 000.90%=324 000 (đồng)
Bạn Lan được trả lại số tiền là
350 000 – 324 000 = 26 000 (đồng)
Giải bài 10 trang 16 SGK Toán 7 Chân trời sáng tạo tập 1
Đường kính của Sao Kim bằng (frac{6}{{25}}) đường kính của Sao Thiên Vương. Đường kính của Sao Thiên Vương bằng (frac{5}{{14}}) đường kính của Sao Mộc.
a) Đường kính của Sao Kim bằng bao nhiêu phần đường kính của Sao Mộc?
b) Biết rằng đường kính của Sao Mộc khoảng 140 000 km, tính đường kính của Sao Kim.
(Theo: https://vi.wikipedia.org/wiki/Hệ Mặt Trời)
Phương pháp giải
a) Nếu A bằng x lần B
B bằng y lần C
Thì A bằng x.y lần C
b) Đường kính của Sao Kim = Đường kính của Sao Mộc. Kết quả của câu a
Lời giải chi tiết
a) Đường kính của Sao Kim bằng số phần đường kính của Sao Mộc là:
(frac{6}{{25}}).(frac{5}{{14}})=(frac{3}{{35}})
Vậy đường kính của Sao Kim bằng (frac{3}{{35}}) đường kính của Sao Mộc.
b) Đường kính của Sao Kim là:
(140,000.frac{3}{{35}} = 12,000) (km)
Vậy đường kính của Sao Kim là 12 000km.
Giải bài 11 trang 16 SGK Toán 7 Chân trời sáng tạo tập 1
Trong tầng đối lưu, nhiệt độ giảm dần theo độ cao. Cứ lên cao 100 m thì nhiệt độ không khí giảm khoảng 0,6 °C (Theo: Sách giáo khoa Địa lí 6 – 2020 – Nhà xuất bản Giáo dục Việt Nam).
a) Tính nhiệt độ không khí bên ngoài một khinh khí cầu đang bay ở độ cao 2,8 km, biết rằng nhiệt độ trên mặt đất lúc đó là 28°C.
b) Nhiệt độ bên ngoài một khinh khí cầu đang bay ở độ cao (frac{{22}}{5}) km bằng – 8,5 °C. Hỏi nhiệt độ trên mặt đất tại vùng trời khinh khí cầu đang bay lúc đó là bao nhiêu độ C?
Phương pháp giải
a) – Đổi đơn vị
– Tính nhiệt độ không khí giảm so với mặt đất ở độ cao 2,8 km.
– Tính nhiệt độ không khí bên ngoài một khinh khí cầu đang bay ở độ cao 2,8 km.
b) – Tính nhiệt độ không khí đã giảm khi ở độ cao – 8,5 °C so với trên mặt đất
– Tính nhiệt độ trên mặt đất tại vùng trời khinh khí cầu đang bay.
Lời giải chi tiết
a) Đổi 2,8 km = 2 800 m
Ở độ cao 2,8 km, nhiệt độ không khí giảm so với mặt đất là:
2 800:100.0,6 =16,8 (°C)
Nhiệt độ không khí bên ngoài một khinh khí cầu đang bay ở độ cao 2,8 km là:
28 – 16,8 = 11,2 (°C)
b) Đổi (frac{{22}}{5}) km = 4 400 m
Nhiệt độ không khí đã giảm khi ở độ cao (frac{{22}}{5}) km so với trên mặt đất là:
4 400:100 . 0,6 = 26,4 (°C)
Nhiệt độ trên mặt đất tại vùng trời khinh khí cầu đang bay là:
(- 8,5) + 26,4 = 17,9 °C
Giải bài 12 trang 17 SGK Toán 7 Chân trời sáng tạo tập 1
Em hãy tìm cách “nối” các số ở những cánh hoa bằng các dấu phép tính cộng, trừ, nhân, chia và dấu ngoặc để được một biểu thức có giá trị đúng bằng số ở nhị hoa.
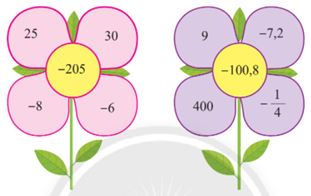
Phương pháp giải
Dùng các dấu phép tính cộng, trừ, nhân, chia, dấu ngoặc để nối các số ở cánh hoa được giá trị là số ở nhị hoa
Lời giải chi tiết
(left( { – 8} right).25 + 30:( – 6) = – 205)
(left( { – frac{1}{4}.400} right) + left( { – 7,2} right):9 = – 100,8)
