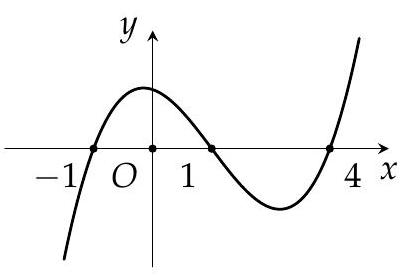
Cho hàm số $f(x)$ có đồ thị hàm số $f^{\prime}(x)$ như hình vẽ dưới đây. Có bao nhiêu số nguyên $m>-10$ để hàm số $y=f(x+m)$ nghịch biến trên $(0 ; 2)$ ?
A. 7 .
B. 5 .
C. 9 .
D. 2 .

Lời giải.
Yêu cầu bài toán
$$
\begin{aligned}
& \Leftrightarrow \quad y^{\prime}=f^{\prime}(x+m) \leq 0, \forall x \in(0 ; 2) \\
& \Leftrightarrow\left[\begin{array}{l}
x+m \leq-1 \\
1 \leq x+m \leq 4
\end{array}, \forall x \in(0 ; 2)\right. \\
& \Leftrightarrow\left[\begin{array}{l}
x \leq-m-1 \\
-m+1 \leq x \leq-m+4
\end{array}, \forall x \in(0 ; 2)\right. \\
& \Leftrightarrow\left[\begin{array}{l}
2 \leq-m-1 \\
\left\{\begin{array}{l}
-m+1 \leq 0 \\
-m+4 \geq 2
\end{array}\right.
\end{array}\right. \\
& \Leftrightarrow\left[\begin{array}{l}
m \leq-3 \\
1 \leq m \leq 2 .
\end{array}\right.
\end{aligned}
$$
Vậy $m \in\{-9 ; \ldots ;-3 ; 1 ; 2\}$.
Suy ra có 9 số nguyên $m$ thỏa đề bài.
