Giải bài tập toán 12 kết nối tri thức bài 1 Tính đơn điệu và cực trị của hàm số chi tiết dễ hiểu giúp các bạn tham khảo và làm bài tập một cách hiệu quả.
Câu 1.1. Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
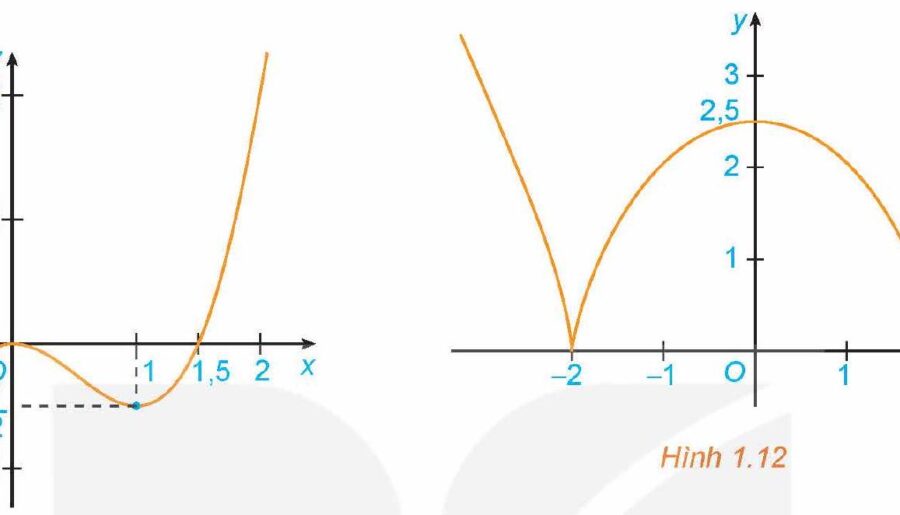
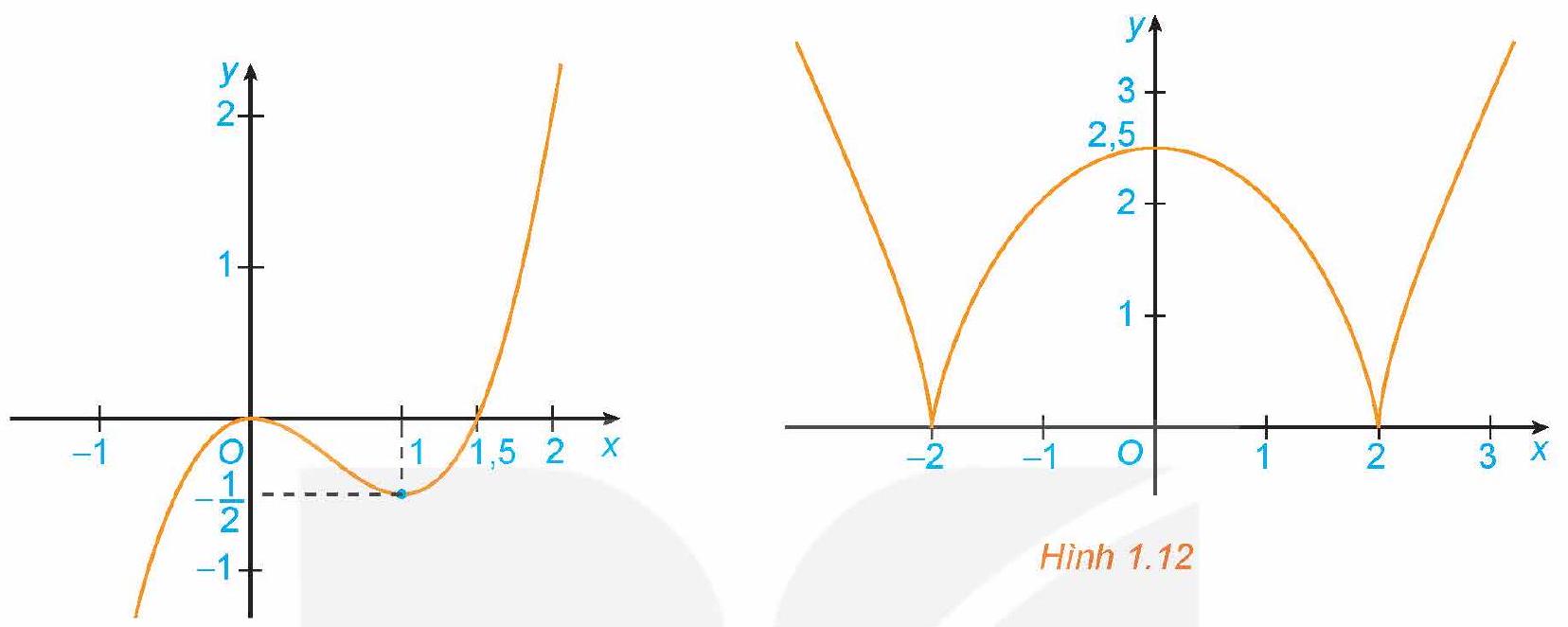
a) Đồ thị hàm số $y = {x^3} – \frac{3}{2}{x^2}$ (Hình 1.11);
b) Đồ thị hàm số $y = \sqrt[3]{{{{\left( {{x^2} – 4} \right)}^2}}}$(Hình 1.12);
Lời giải:
Phương pháp:
+ Nếu đồ thị hàm số “đi lên” từ trái sang phải trên khoảng (a;b) thì hàm số đồng biến trên khoảng (a;b)
+ Nếu đồ thị hàm số “đi xuống” từ trái sang phải trên khoảng (a;b) thì hàm số nghịch biến trên khoảng (a;b)
a) + Hàm số đồng biến trên khoảng $\left( { – \infty ;0} \right)$ và $\left( {1; + \infty } \right)$.
+ Hàm số nghịch biến trên khoảng $\left( {0;1} \right)$.
b) + Hàm số đồng biến trên khoảng $\left( { – 2;0} \right)$ và $\left( {2; + \infty } \right)$.
+ Hàm số nghịch biến trên khoảng $\left( { – \infty ; – 2} \right)$ và $\left( {0;2} \right)$.
Câu 1.2. Xét sự đồng biến, nghịch biến của các hàm số sau:
a) $y = \frac{1}{3}{x^3} – 2{x^2} + 3x + 1$;
b) $y = – {x^3} + 2{x^2} – 5x + 3$.
Lời giải:
a) Tập xác định $D = \mathbb{R}$
$y’ = {x^2} – 4x + 3$
$y’ = 0 \Leftrightarrow {x^2} – 4x + 3 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 3 \hfill \\
x = 1 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
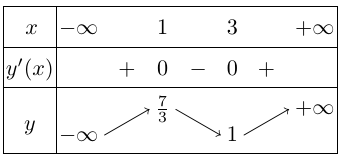
Vậy,
+ Hàm số đồng biến trên các khoảng $( – \infty ;1)$ và $(3; + \infty )$.
+ Hàm số nghịch biến trên khoảng $(1;3)$.
b) Tập xác định $D = \mathbb{R}$
$y’ = – 3{x^2} + 4x – 5$
$y’ = 0 \Leftrightarrow – 3{x^2} + 4x – 5 = 0$ (phương trình vô nghiệm)
Bảng biến thiên
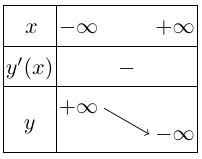
Vậy,
+ Hàm số nghịch biến trên khoảng $( – \infty ; + \infty )$.
Câu 1.3. Tìm các khoảng đơn điệu của các hàm số sau:
a) $y = \frac{{2x – 1}}{{x + 2}}$
b) $y = \frac{{{x^2} + x + 4}}{{x – 3}}$.
Lời giải:
a) $y = \frac{{2x – 1}}{{x + 2}}$
Tập xác định $D = \mathbb{R}\backslash \left\{ { – 2} \right\}$
Áp dụng công thức tính đạo hàm: ${\left( {\frac{{ax + b}}{{cx + d}}} \right)^\prime } = \frac{{a.d – c.b}}{{{{\left( {cx + d} \right)}^2}}}$
$y’ = \frac{{2.2 – 1.( – 1)}}{{{{(x + 2)}^2}}} = \frac{5}{{{{(x + 2)}^2}}}$
$y’ > 0,\,\forall x \in D$
Bảng biến thiên
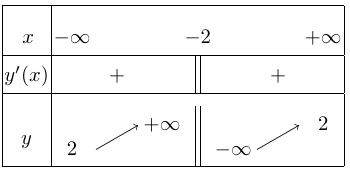
Vậy,
+ Hàm số đồng biến trên các khoảng $( – \infty ; – 2)$ và $(-2; + \infty )$
b) $y = \frac{{{x^2} + x + 4}}{{x – 3}}$.
Tập xác định $D = \mathbb{R}\backslash \left\{ 3 \right\}$
Áp dụng công thức tính đạo hàm: ${\left( {\frac{u}{v}} \right)^\prime } = \frac{{u’.v – u.v’}}{{{v^2}}}$
$y’ = \frac{{({x^2} + x + 4)'(x – 3) – ({x^2} + x + 4)(x – 3)’}}{{{{(x – 3)}^2}}}$
$ = \frac{{(2x + 1).(x – 3) – ({x^2} + x + 4).1}}{{{{(x – 3)}^2}}}$
$ = \frac{{2{x^2} – 6x + x – 3 – {x^2} – x – 4}}{{{{(x – 3)}^2}}}$
$ = \frac{{{x^2} – 6x – 7}}{{{{(x – 3)}^2}}}$
$y’ = 0 \Rightarrow {x^2} – 6x – 7 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 7 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
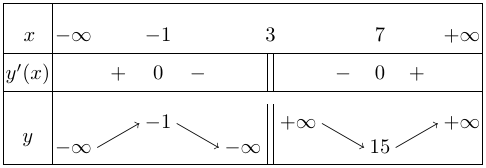
Vậy,
+ Hàm số đồng biến trên các khoảng $( – \infty ; – 1)$ và $(7; + \infty )$.
+ Hàm số nghịch biến trên các khoảng $( – 1;3)$ và $(3;7)$.
Câu 1.4. Xét chiều biến thiên của các hàm số sau:
a) $y = \sqrt {4 – {x^2}} $;
b) $y = \frac{x}{{{x^2} + 1}}$.
Lời giải:
a) $y = \sqrt {4 – {x^2}} $;
Tập xác định $D = [ – 2;2]$
Áp dụng công thức tính đạo hàm: ${\left( {\sqrt u } \right)^\prime } = \frac{{u’}}{{2\sqrt u }}$
$y’ = \frac{{(4 – {x^2})’}}{{2\sqrt {4 – {x^2}} }} = \frac{{ – 2x}}{{2\sqrt {4 – {x^2}} }} = \frac{{ – x}}{{\sqrt {4 – {x^2}} }}$
$y’ = 0 \Rightarrow – x = 0 \Leftrightarrow x = 0$
Bảng biến thiên
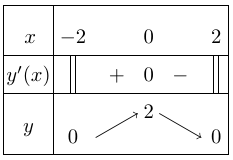
Vậy,
+ Hàm số đồng biến trên khoảng $( – 2;0)$.
+ Hàm số nghịch biến trên khoảng $(0;2)$.
b) $y = \frac{x}{{{x^2} + 1}}$.
Tập xác định $D = \mathbb{R}$.
Áp dụng công thức tính đạo hàm: ${\left( {\frac{u}{v}} \right)^\prime } = \frac{{u’.v – u.v’}}{{{v^2}}}$
$y’ = \frac{{(x)’.({x^2} + 1) – x.({x^2} + 1)’}}{{{{({x^2} + 1)}^2}}}$
$ = \frac{{1.({x^2} + 1) – x.2x}}{{{{({x^2} + 1)}^2}}} = \frac{{1.({x^2} + 1) – 2{x^2}}}{{{{({x^2} + 1)}^2}}}$
$ = \frac{{ – {x^2} + 1}}{{{{({x^2} + 1)}^2}}}$
$y’ = 0 \Rightarrow – {x^2} + 1 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
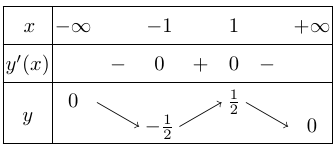
+ Hàm số đồng biến trên khoảng $( – 1;1)$.
+ Hàm số nghịch biến trên các khoảng $( – \infty ; – 1)$ và $(1; + \infty )$.
Câu 1.5. Giả sử số dân của một thị trấn sau $t$ năm kể từ năm 2000 được mô tả bởi hàm số $N\left( t \right) = \frac{{25t + 10}}{{t + 5}},t \geqslant 0$
trong đó $N\left( t \right)$ được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm $N’\left( t \right)$ và $\mathop {\lim }\limits_{t \to + \infty } N(t)$. Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
Lời giải:
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
+ Số dân của thị trấn đó vào năm 2000 là $N\left( 0 \right) = \frac{{25.0 + 10}}{{0 + 5}} = 2$ (nghìn người).
+ Số dân của thị trấn đó vào năm 2015 là $N\left( {15} \right) = \frac{{25.15 + 10}}{{15 + 5}} = 19,25$ (nghìn người).
b) Tính đạo hàm $N’\left( t \right)$ và $\mathop {\lim }\limits_{t \to + \infty } N(t)$. Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.
+ Tính đạo hàm:
Áp dụng công thức tính đạo hàm: ${\left( {\frac{{ax + b}}{{cx + d}}} \right)^\prime } = \frac{{a.d – c.b}}{{{{\left( {cx + d} \right)}^2}}}$
Ta có:
$N’\left( t \right) = \frac{{25.5 – 1.10}}{{{{(t + 5)}^2}}} = \frac{{115}}{{{{(t + 5)}^2}}} > 0,\,\forall t \geqslant 0$ (1)
+ $\mathop {\lim }\limits_{t \to + \infty } N(t) = \mathop {\lim }\limits_{t \to + \infty } \frac{{25t + 10}}{{t + 5}} = \frac{{25}}{1} = 25$ (2)
+ Từ (1) suy ra hàm số $N(t)$ đồng biến nên dân số thị trấn đó tăng.
+ Từ (2) suy ra dân số thị trấn đó không vượt 25 (nghìn người).
Câu 1.6. Đồ thị của đạo hàm bậc nhất $y = f’\left( x \right)$ của hàm số $f\left( x \right)$ được cho trong Hình 1.13.
a) Hàm số $f\left( x \right)$ đồng biến trên những khoảng nào? Giải thích.
b) Tại giá trị nào của $x$ thì $f\left( x \right)$ có cực đại hoặc cực tiểu? Giải thích.
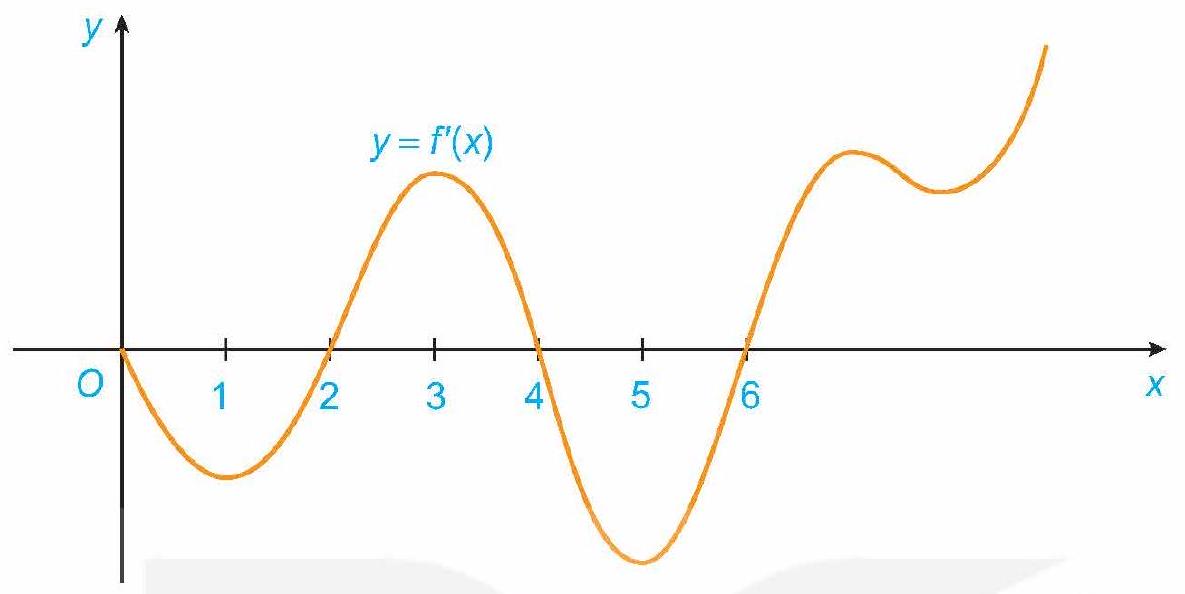
Hình 1.13
Lời giải:
Phương pháp
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0$ nên hàm số $y = f(x)$ đồng biến trên khoảng $(a;b)$.
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía dưới trục hoành thì $f'(x) < 0$ nên hàm số $y = f(x)$ nghịch biến trên khoảng $(a;b)$.
+ Nếu đồ thị hàm số $y = f'(x)$ cắt trục hoành tại điểm ${x_0}$ thì $f'({x_0}) = 0$.
a) Hàm số $f\left( x \right)$ đồng biến trên các khoảng: $\left( { – \infty ;0} \right)$, $\left( {2;4} \right)$; $\left( {6; + \infty } \right)$.
Giải thích: Trên các khoảng đó đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0$ nên hàm số $y = f(x)$ đồng biến.
b) Tại giá trị nào của $x$ thì $f\left( x \right)$ có cực đại hoặc cực tiểu? Giải thích.
Dựa vào đồ thị hàm số $y=f\left( x \right)$ ta có bảng xét dấu $f'(x)$ :

Vậy,
+ Hàm số đạt cực đại tại các điểm $x = 0;\,x = 4$.
+ Hàm số đạt cực tiểu tại các điểm $x = 2;\,x = 6$.
Câu 1.7. Tìm cực trị của các hàm số sau:
a) $y = 2{x^3} – 9{x^2} + 12x – 5$;
b) $y = {x^4} – 4{x^2} + 2$;
c) $y = \frac{{{x^2} – 2x + 3}}{{x – 1}}$;
d) $y = \sqrt {4x – 2{x^2}} $.
Lời giải:
a) $y = 2{x^3} – 9{x^2} + 12x – 5$;
Tập xác định $D = \mathbb{R}$
$y’ = 6{x^2} – 18x + 12$
$y’ = 0 \Leftrightarrow 6{x^2} – 18x + 12 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 2 \hfill \\
x = 1 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
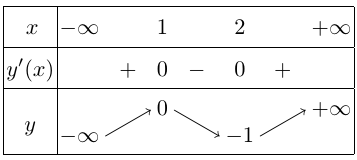
Vậy,
+ Hàm số đạt cực đại tại $x = 1$ và ${y_{CD}} = y(1) = 0$.
+ Hàm số đạt cực tiểu tại $x = 2$ và ${y_{CT}} = y(2) = – 1$.
b) $y = {x^4} – 4{x^2} + 2$;
Tập xác định $D = \mathbb{R}$
$y’ = 4{x^3} – 8x$
$y’ = 0 \Leftrightarrow 4{x^3} – 8x = 0 \Leftrightarrow \left[ \begin{gathered}
x = \sqrt 2 \hfill \\
x = 0 \hfill \\
x = – \sqrt 2 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
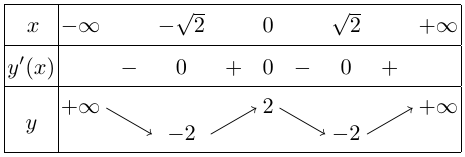
Vậy,
+ Hàm số đạt cực đại tại $x = 0$ và ${y_{CD}} = y(0) = 2$.
+ Hàm số đạt cực tiểu tại $x = \pm \sqrt 2 $ và ${y_{CT}} = y( \pm \sqrt 2 ) = – 2$.
c) $y = \frac{{{x^2} – 2x + 3}}{{x – 1}}$;
Tập xác định $D = \mathbb{R}\backslash \left\{ 1 \right\}$
Áp dụng công thức tính đạo hàm: ${\left( {\frac{u}{v}} \right)^\prime } = \frac{{u’.v – u.v’}}{{{v^2}}}$
$y’ = \frac{{({x^2} – 2x + 3)’.(x – 1) – ({x^2} – 2x + 3).(x – 1)’}}{{{{(x – 1)}^2}}}$
$ = \frac{{(2x – 2).(x – 1) – ({x^2} – 2x + 3).1}}{{{{(x – 1)}^2}}}$
$ = \frac{{2{x^2} – 2x – 2x + 2 – {x^2} + 2x – 3}}{{{{(x – 1)}^2}}} = \frac{{{x^2} – 2x – 1}}{{{{(x – 1)}^2}}}$
$y’ = 0 \Rightarrow {x^2} – 2x – 1 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 + \sqrt 2 \hfill \\
x = 1 – \sqrt 2 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
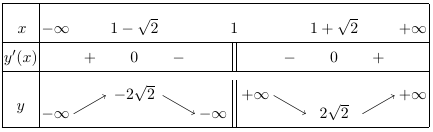
Vậy,
+ Hàm số đạt cực đại tại $x = 1 – \sqrt 2 $ và ${y_{CD}} = y(1 – \sqrt 2 ) = – 2\sqrt 2 $.
+ Hàm số đạt cực tiểu tại $x = 1 + \sqrt 2 $ và ${y_{CT}} = = y(1 + \sqrt 2 ) = 2\sqrt 2 $.
d) $y = \sqrt {4x – 2{x^2}} $
Tập xác định $D = [0;2]$
Áp dụng công thức tính đạo hàm: ${\left( {\sqrt u } \right)^\prime } = \frac{{u’}}{{2\sqrt u }}$
$y’ = \frac{{(4x – 2{x^2})’}}{{2\sqrt {4x – 2{x^2}} }} = \frac{{4 – 4x}}{{2\sqrt {4x – 2{x^2}} }} = \frac{{2 – 2x}}{{\sqrt {4x – 2{x^2}} }}$
$y’ = 0 \Rightarrow 2 – 2x = 0 \Leftrightarrow x = 1$
Bảng biến thiên
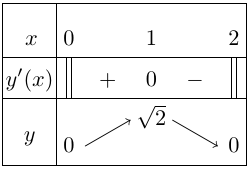
Vậy,
+ Hàm số đạt cực đại tại $x = 1$ và ${y_{CD}} = y(1) = \sqrt 2 $.
+ Hàm số không có cực tiểu.
Câu 1.8. Cho hàm số $y = f\left( x \right) = \left| x \right|$.
a) Tính các giới hạn $\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f(x) – f(0)}}{{x – 0}}$ và$\mathop {\lim }\limits_{x \to {0^ – }} \frac{{f(x) – f(0)}}{{x – 0}}$.
Từ đó suy ra hàm số không có đạo hàm tại $x = 0$.
b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại $x = 0$ (xem Hình 1.4).
Lời giải:
a) Tính các giới hạn:
* $\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f(x) – f(0)}}{{x – 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left| x \right| – \left| 0 \right|}}{{x – 0}}$
$ = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left| x \right|}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{x} = \mathop {\lim }\limits_{x \to {0^ + }} 1 = 1$
* $\mathop {\lim }\limits_{x \to {0^ – }} \frac{{f(x) – f(0)}}{{x – 0}} = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{\left| x \right| – \left| 0 \right|}}{{x – 0}}$
$ = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{\left| x \right|}}{x} = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{ – x}}{x} = \mathop {\lim }\limits_{x \to {0^ – }} \left( { – 1} \right) = – 1$
Suy ra, $\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f(x) – f(0)}}{{x – 0}} \ne \mathop {\lim }\limits_{x \to {0^ – }} \frac{{f(x) – f(0)}}{{x – 0}}$
Nên hàm số không có đạo hàm tại $x = 0$.
b)
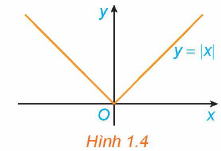
Ta có: $y=f(x)=|x|= \begin{cases}-x & \text { khi } x \in(-\infty ; 0) \\ x & \text { khi } x \in(0 ;+\infty)\end{cases}$
Hàm số $y=f(x)=|x|$ liên tục và xác định trên $(-\infty ;+\infty)$
Với số $h>0$ ta có: Với $x \in(-h ; h) \subset(-\infty ;+\infty)$ và $x \neq 0$ thì $y=f(x)=|x|>0=f(0)$
Do vậy, hàm số $y=f(x)=|x|$ có cực tiểu là $x=0$.
Câu 1.9. Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số
$f\left( t \right) = \frac{{5000}}{{1 + 5{e^{ – t}}}},t \geqslant 0$
trong đó thời gian $t$ được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm $f’\left( t \right)$ sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Lời giải:
Ta có: ${f^\prime }(t) = \frac{{ – 5000{{\left( {1 + 5{e^{ – t}}} \right)}^\prime }}}{{{{\left( {1 + 5{e^{ – t}}} \right)}^2}}} = \frac{{25000{e^{ – t}}}}{{{{\left( {1 + 5{e^{ – t}}} \right)}^2}}}$
Tốc độ bán hàng là lớn nhất khi ${f^\prime }(t)$ lớn nhất.
Đặt $h(t) = \frac{{25000{e^{ – t}}}}{{{{\left( {1 + 5{e^{ – t}}} \right)}^2}}}$.
${h^\prime }(t) = \frac{{ – 25000{e^{ – t}}{{\left( {1 + 5{e^{ – t}}} \right)}^2} – 2 \cdot \left( { – 5{e^{ – t}}} \right) \cdot \left( {1 + 5{e^{ – t}}} \right) \cdot 25000{e^{ – t}}}}{{{{\left( {1 + 5{e^{ – t}}} \right)}^4}}}$
$ = \frac{{ – 25000{e^{ – t}}\left( {1 + 5{e^{ – t}}} \right)\left( {1 + 5{e^{ – t}} – 10{e^{ – t}}} \right)}}{{{{\left( {1 + 5{e^{ – t}}} \right)}^4}}} = \frac{{ – 25000{e^{ – t}}\left( {1 – 5{e^{ – t}}} \right)}}{{ = {{\left( {1 + 5{e^{ – t}}} \right)}^3}}}$
${h^\prime }(t) = 0 \Leftrightarrow \frac{{ – 25000{e^{ – t}}\left( {1 – 5{e^{ – t}}} \right)}}{{{{\left( {1 + 5{e^{ – t}}} \right)}^3}}} = 0 \Leftrightarrow 1 – 5{e^{ – t}} = 0 \Leftrightarrow {e^{ – t}} = \frac{1}{5} \Leftrightarrow t = \ln 5$ (thỏa mãn)
Ta có bảng biến thiên với $t \in [0; + \infty )$ :
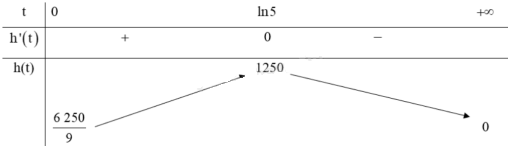
Vậy, sau khi phát hành khoảng $\ln 5 \approx 1,6$ năm thì tốc độ bán hàng là lớn nhất.
———-