.tdi_279.td-a-rec{text-align:center}.tdi_279.td-a-rec:not(.td-a-rec-no-translate){transform:translateZ(0)}.tdi_279 .td-element-style{z-index:-1}.tdi_279.td-a-rec-img{text-align:left}.tdi_279.td-a-rec-img img{margin:0 auto 0 0}@media (max-width:767px){.tdi_279.td-a-rec-img{text-align:center}}
Giải Toán 12 Chân Trời Sáng Tạo Chương 5 Phương Trình Mặt Phẳng, Đường Thẳng, Mặt Cầu
- Giải Toán 12 Chân Trời Sáng Tạo Bài 1 Chương 5 Phương Trình Mặt Phẳng
- Giải Toán 12 Chân Trời Sáng Tạo Bài 2 Chương 5 Phương Trình Đường Thẳng Trong Không Gian
- Giải Toán 12 Chân Trời Sáng Tạo Bài 3 Chương 5 Phương Trình Mặt Cầu
- Giải Toán 12 Chân Trời Sáng Tạo Bài Tập Cuối Chương 5
Câu 1. Viết phương trình mặt cầu $S$ :
a) Có tâm $I\left( {7; – 3;0} \right)$, bán kính $R = 8$;
b) Có tâm $M\left( {3;1; – 4} \right)$ và đi qua điểm $N\left( {1;0;1} \right)$;
c) Có đường kính $AB$ với $A\left( {4;6;8} \right)$ và $B\left( {2;4;4} \right)$.
Lời giải
Câu 2. Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a) ${x^2} + {y^2} + {z^2} + 5x – 7y + z – 1 = 0$;
b) ${x^2} + {y^2} + {z^2} + 4x + 6y – 2z + 100 = 0$;
c) ${x^2} + {y^2} + {z^2} – x – y – z + \frac{1}{2} = 0$.
Lời giải
Câu 3. Cho hai điểm $A\left( {1;0;0} \right)$ và $B\left( {5;0;0} \right)$. Chứng minh rằng nếu điểm $M\left( {x;y;z} \right)$ thoả mãn $\overrightarrow {MA} \cdot \overrightarrow {MB} = 0$ thì $M$ thuộc một mặt cầu $\left( S \right)$. Tìm tâm và bán kính của $\left( S \right)$.
Lời giải
Câu 4. Phần mềm mô phỏng thiết bị thám hiểm đại dương có dạng hình cầu trong không gian $Oxyz$. Cho biết tọa độ tâm mặt cầu là $I\left( {360;200;400} \right)$ và bán kính $r = 2\;m$. Viết phương trình mặt cầu.

Hình 9
Lời giải
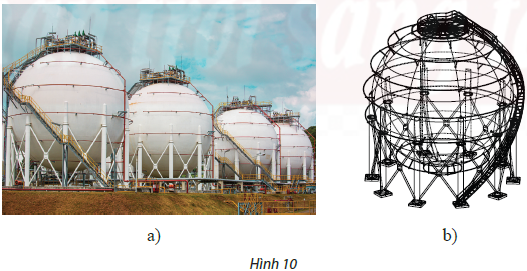
Câu 5. Người ta muốn thiết kế một bồn chứa khí hoá lỏng hình cầu bằng phần mềm $3D$. Cho biết phương trình bề mặt của bồn chứa là $\left( S \right):{(x – 6)^2} + {(y – 6)^2} + {(z – 6)^2} = 25$. Phương trình mặt phẳng chứa nắp là $\left( P \right):z = 10$.
a) Tìm tâm và bán kính của bồn chứa.
b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng chứa nắp.
Lời giải
.tdi_280.td-a-rec{text-align:center}.tdi_280.td-a-rec:not(.td-a-rec-no-translate){transform:translateZ(0)}.tdi_280 .td-element-style{z-index:-1}.tdi_280.td-a-rec-img{text-align:left}.tdi_280.td-a-rec-img img{margin:0 auto 0 0}@media (max-width:767px){.tdi_280.td-a-rec-img{text-align:center}}
———-
SGK T12 CTST
