[4] Trong không gian tọa độ (Oxyz), cho hai mặt cầu (left( {{S_1}} right):{x^2} + {left( {y – 1} right)^2} + {left( {z – 2} right)^2} = 16),(left( {{S_2}} right):{left( {x – 1} right)^2} + {left( {y + 1} right)^2} + {z^2} = 1) và điểm (Aleft( {frac{4}{3};frac{7}{3}; – frac{{14}}{3}} right)). Gọi (I) là tâm […]
[4] Trong không gian (Oxyz,) cho mặt cầu (left( S right)) có phương trình ({left( {x – 3} right)^2} + {left( {y – 4} right)^2} + {left( {z – 4} right)^2} = 25) và điểm (Aleft( {0,;,1,;,9} right)). Gọi đường tròn (left( C right)) là giao tuyến của mặt cầu (left( S right)) với mặt […]
[4] Trong không gian (Oxyz,) cho điểm (Aleft( {2,; – ,1,; – 3} right))và mặt cầu (left( S right)) có phương trình: (,{left( {x – 4} right)^2} + {left( {y – 3} right)^2} + {left( {z – 4} right)^2} = 25.) Gọi (left( C right)) là giao tuyến của (left( S right))với mặt phẳng (left( […]
[Mức độ 4] Cho hàm số (y = fleft( x right)) có đạo hàm (f’left( x right) = {x^2} + x – 6) với mọi (x in mathbb{R}). Gọi (S) là tập hợp các giá trị nguyên của tham số (m) sao cho ứng với mỗi (m), hàm số (gleft( x right) = fleft( {{x^3} […]
[Mức độ 3] Cho hàm số (y, = ,f(x),) có đạo hàm và liên tục trên (mathbb{R}) thỏa mãn (fleft( { – 6} right) = 42) và bảng xét dấu đạo hàm như Giá trị nhỏ nhất của hàm số (y, = ,fleft( { – ,3{x^4},, + ,,12{x^2}, – ,15} right), + ,2{x^6}, + ,6{x^4}, […]
[Mức độ 4] Cho hàm số đa thức (y = fleft( x right)) có đạo hàm trên (mathbb{R}). Biết rằng (fleft( 0 right) = 0), (fleft( { – 3} right) = fleft( {frac{3}{2}} right) = – frac{{19}}{4}) và đồ thị hàm số (y = f’left( x right)) có dạng như hình vẽ. Hàm số (gleft( […]
Một con búp bê cầu mưa có dạng khối tròn xoay được tạo thành khi quay miền (left( R right)) quanh trục (Ox). Miền (left( R right)) được giới hạn bởi nửa đường tròn và một phần của đồ thị hàm số (y = sqrt {2x – 1} left( {1 le x le 5} right)) […]
Cho hai số dương (x,,y) thoả mãn ({log _2}{left( {4x + y + 2xy + 2} right)^{y + 2}} = 8 – left( {2x – 2} right)left( {y + 2} right)). Giá trị nhỏ nhất của (P = 2x + y) là số có dạng (M = asqrt b + c) với (a,,b in mathbb{N},,a […]
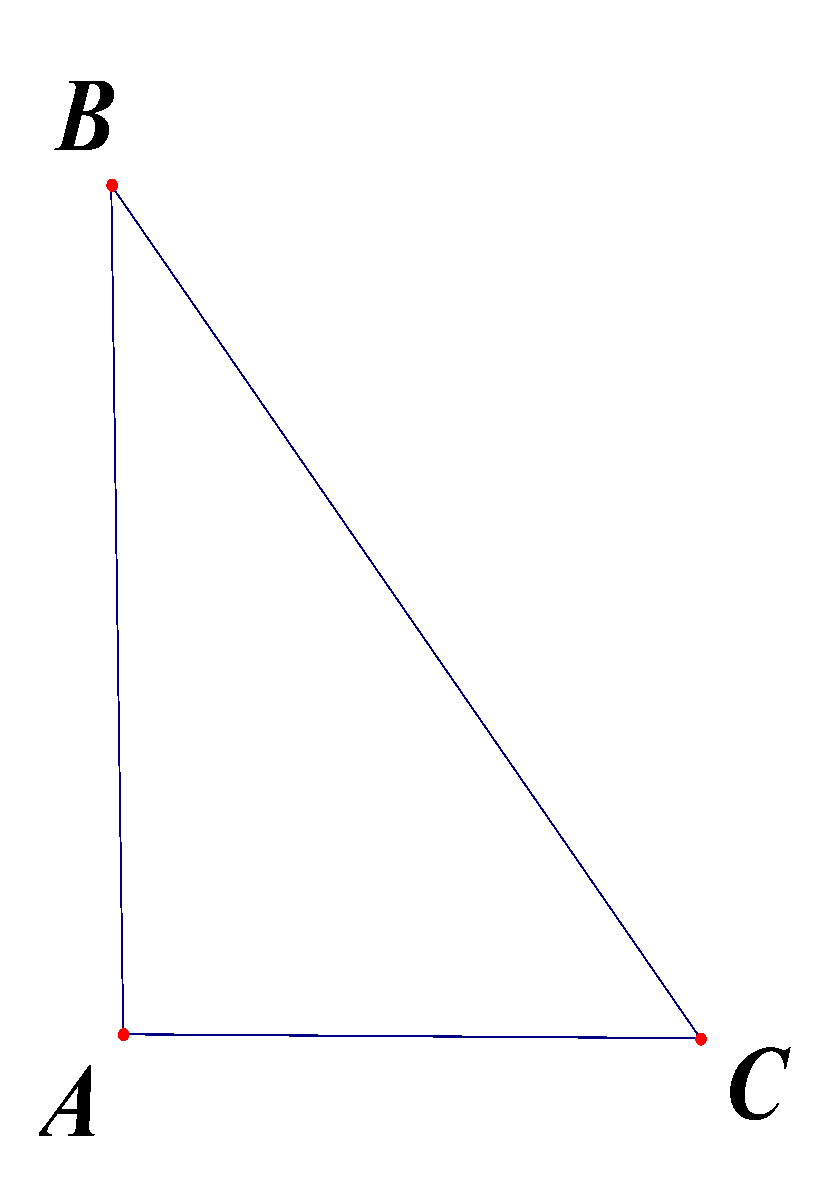
Trong không gian, cho tam giác \(ABC\) vuông tại\(A\),\(AB = a\) và\(BC = 2a\). Tính thể tích khối nón nhận được khi quay tam giác \(ABC\) xung quanh cạnh \(l = 2a\). A. \(V = \pi {a^3}\). B. \(V = \sqrt 3 \pi {a^3}\). C. \(V = \frac{{\sqrt 3 \pi {a^3}}}{9}\). D. \(V = \frac{{\sqrt […]
Quay một hình vuông cạnh \(7\)cm quanh một cạnh của nó ta được một hình trụ. Diện tích toàn phần của hình trụ thu được là A. \(343\pi \;c{m^2}\). B. \(49\pi \;c{m^2}\). C. \(98\pi \;c{m^2}\). D. \(196\pi \;c{m^2}\). Lời giải: Hình trụ có bán kính \(r = 7\)cm, và chiều cao\(h = 7\)cm. Vậy \({S_{tp}} […]