Cách Chứng minh hai đường thẳng vuông góc bằng cách chứng minh đường thẳng này vuông góc với mặt phẳng chứa đường thẳng kia.
Phương pháp giải:
– Muốn chứng minh đường thẳng a vuông góc với đường thẳng b, ta đi tìm mặt phẳng (β) chứa đường thẳng b sao cho việc chứng minh a $bot $ (β) dễ thực hiện.
– Sử dụng định lý ba đường vuông góc.
Bài tập về chứng minh quan hệ vuông góc trong không gian có đáp án chi tiết
| Bài tập 1: Cho tứ diện đều ABCD. Chứng minh các cặp cạnh đối diện của tứ diện này vuông góc với nhau từng đôi một. |
Lời giải chi tiết
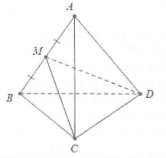
Gọi M là trung điểm của AB
Tứ diện ABCD đều nên ∆ABD và ∆ABC là các tam giác đều suy ra $left{ begin{array} {} DMbot AB \ {} CMbot AB \ end{array} right.Rightarrow ABbot (MCD)$
Do đó $ABbot CD$
Chứng minh tương tự ta cũng có $BCbot AD,ACbot BD$
| Bài tập 2: Hình chóp S.ABCD có cạnh SA vuông góc với mặt phẳng (ABCD) và đáy ABCD là hình thang vuông tại A và D với $AD=CD=frac{AB}{2}$
a) Gọi I là trung điểm của đoạn AB, chứng minh $CIbot AB$ và $DIbot SC$ b) Chứng minh các mặt bên của hình chóp S.ABCD là các tam giác vuông. |
Lời giải chi tiết
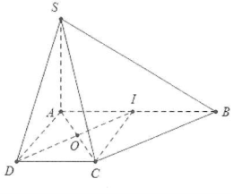
a) Đặt AB = 2a $Rightarrow $ AD = CD = a
Do AB = 2CD $Rightarrow $ AI = AD = CD = CI = a
Khi đó AICD là hình vuông cạnh a.
Do đó $CIbot AB$
Mặt khác $left{ begin{array} {} ACbot DI \ {} DIbot SA \ end{array} right.Rightarrow DIbot (SAC)Rightarrow DIbot SC$
b) Do $SAbot (ABCD)Rightarrow Delta SAD,Delta SAB$ vuông tại S.
Mặt khác $left{ begin{array} {} CDbot AD \ {} CDbot SA \ end{array} right.Rightarrow CDbot (SAD)Rightarrow CDbot SD$
nên ∆SDC vuông tại D.
Xét ∆ACD có trung tuyến $CI=frac{AB}{2}Rightarrow Delta ACD$vuông tại C$Rightarrow BCbot AC$
Mặt khác $BCbot SARightarrow BCbot (SAC)Rightarrow BCbot SCRightarrow Delta SCB$vuông tại C.
| Bài tập 3: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Cạnh bên CC’ vuông góc với đáy và CC’ = a.
a) Gọi I là trung điểm của BC. Chứng minh $AIbot BC’$ b) Gọi M là trung điểm của BB’. Chứng minh $BC’bot AM$ c) Gọi K là điểm trên đoạn A’B’ sao cho $B’K=frac{a}{4}$ và J là trung điểm của B’C’. Chứng minh rằng: $AMbot MK$ và $AMbot KJ$ |
Lời giải chi tiết
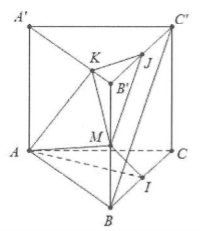
a) Do ∆ABC là tam giác đều và I là trung điểm của BC nên $AIbot BC$
Mặt khác $AIbot CC’Rightarrow AIbot (BCC’B’)Rightarrow AIbot BC’$
b) Dễ thấy BCC’B’ là hình vuông nên $B’Cbot BC’$
Mặt khác MI là đường trung bình trong tam giác B’BC nên MI//B’C suy ra $MIbot BC’$
Lại có: $AIbot BC’Rightarrow BC’bot (AIM)Rightarrow BC’bot AM$
c) Ta có: $tan widehat{KMB’}=frac{KB’}{MB’}=frac{1}{2};tan widehat{AMB}=frac{AB}{BM}=2$
Suy ra $tan widehat{KMB’}=cot widehat{AMB}Rightarrow widehat{KMB’}+widehat{AMB}={{90}^{circ }}$
Do đó $widehat{AMK}={{90}^{circ }}Rightarrow AMbot MK$
Mặt khác $left{ begin{array} {} AMbot BC’ \ {} MJ//BC’ \ end{array} right.Rightarrow AMbot MJ$
Suy ra $AMbot (MKJ)Rightarrow AMbot KJ$
| Bài tập 4: Cho hình chóp đều S.ABCD đáy ABCD là hình vuông, gọi E là điểm đối xứng của D qua trung điểm của SA. Gọi M, N lần lượt là trung điểm của AE và BC. Chứng minh rằng $MNbot BD$ |
Lời giải chi tiết
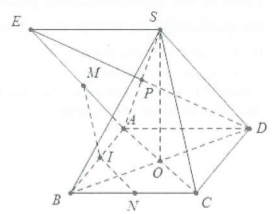
Gọi I, P lần lượt là trung điểm của AB và SA, O là giao điểm của AC và BD.
Ta có: $left{ begin{array} {} IN//AC \ {} ACbot BD \ end{array} right.Rightarrow BDbot IN$ (1)
Mặt khác $left{ begin{array} {} IM//BE \ {} BEbot PO \ end{array} right.Rightarrow IMbot PO$ (*)
Mà $PObot BD$ (**) (Do ∆BPD là tam giác cân tại P có đường trung tuyến PO).
Từ (*) và (**) ta có: $BDbot IM$ (2)
Từ (1) và (2) ta có: $BDbot (IMN)Rightarrow BDbot MN$
