Giải bài tập Bài 5: Giá trị lượng giác của một góc từ 0˚ đến 180˚ (Kết nối) – Sách Toán

adsense

Giải bài tập Bài 5: Giá trị lượng giác của một góc từ 0˚ đến 180˚ (Kết nối)
============

Giải bài 3.1 trang 37 SGK Toán 10 Kết nối tri thức tập 1

Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau:

a) (left( {2sin {{30}^o} + cos {{135}^o} – 3tan {{150}^o}} right).left( {cos {{180}^o} – cot {{60}^o}} right))

b) ({sin ^2}{90^o} + {cos ^2}{120^o} + {cos ^2}{0^o} – {tan ^2}60 + {cot ^2}{135^o})

c) (cos {60^o}.sin {30^o} + {cos ^2}{30^o})

 

Giải bài 3.1 trang 37 SGK Toán 10 Kết nối tri thức tập 1

Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau:

a) (left( {2sin {{30}^o} + cos {{135}^o} – 3tan {{150}^o}} right).left( {cos {{180}^o} – cot {{60}^o}} right))

b) ({sin ^2}{90^o} + {cos ^2}{120^o} + {cos ^2}{0^o} – {tan ^2}60 + {cot ^2}{135^o})

c) (cos {60^o}.sin {30^o} + {cos ^2}{30^o})

Phương pháp giải

a) Bước 1: Đưa GTLG của các góc ({135^o},{150^o},{180^o}) về GTLG của các góc ({45^o},{30^o},{0^o})

(cos {135^o} =  – cos {45^o};cos {180^o} =  – cos {0^o}\tan {150^o} =  – tan {30^o})

Bước 2: Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.

(sin {30^o} = frac{1}{2};tan {30^o} = frac{{sqrt 3 }}{3}\cos {45^o} = frac{{sqrt 2 }}{2};cos {0^o} = 1;cot {60^o} = frac{{sqrt 3 }}{3})

b) Bước 1: Đưa GTLG của các góc ({120^o},{135^o}) về GTLG của các góc ({60^o},{45^o})

(cos {120^o} =  – cos {60^o}, cot {135^o} =  – cot {45^o})

Bước 2: Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.

(cos {0^o} = 1;;;cot {45^o} = 1;;;cos {60^o} = frac{1}{2}\tan {60^o} = sqrt 3 ;;;sin {90^o} = 1)

c) Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.

(sin {30^o} = frac{1}{2};;;cos {30^o} = frac{{sqrt 3 }}{2};;cos {60^o} = frac{1}{2};)

Hướng dẫn giải

a) Đặt  (A = left( {2sin {{30}^o} + cos {{135}^o} – 3tan {{150}^o}} right).left( {cos {{180}^o} – cot {{60}^o}} right))

Ta có: (left{ begin{array}{l}cos {135^o} =  – cos {45^o};cos {180^o} =  – cos {0^o}\tan {150^o} =  – tan {30^o}end{array} right.)

( Rightarrow A = left( {2sin {{30}^o} – cos {{45}^o} + 3tan {{30}^o}} right).left( { – cos {0^o} – cot {{60}^o}} right))

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

(left{ begin{array}{l}sin {30^o} = frac{1}{2};tan {30^o} = frac{{sqrt 3 }}{3}\cos {45^o} = frac{{sqrt 2 }}{2};cos {0^o} = 1;cot {60^o} = frac{{sqrt 3 }}{3}end{array} right.)

( Rightarrow A = left( {2.frac{1}{2} – frac{{sqrt 2 }}{2} + 3.frac{{sqrt 3 }}{3}} right).left( { – 1 – frac{{sqrt 3 }}{3}} right))

(begin{array}{l} Leftrightarrow A =  – left( {1 – frac{{sqrt 2 }}{2} + sqrt 3 } right).left( {1 + frac{{sqrt 3 }}{3}} right)\ Leftrightarrow A =  – frac{{2 – sqrt 2  + 2sqrt 3 }}{2}.frac{{3 + sqrt 3 }}{3}\ Leftrightarrow A =  – frac{{left( {2 – sqrt 2  + 2sqrt 3 } right)left( {3 + sqrt 3 } right)}}{6}\ Leftrightarrow A =  – frac{{6 + 2sqrt 3  – 3sqrt 2  – sqrt 6  + 6sqrt 3  + 6}}{6}\ Leftrightarrow A =  – frac{{12 + 8sqrt 3  – 3sqrt 2  – sqrt 6 }}{6}.end{array})

b)

Đặt  (B = {sin ^2}{90^o} + {cos ^2}{120^o} + {cos ^2}{0^o} – {tan ^2}60 + {cot ^2}{135^o})

Ta có: (left{ begin{array}{l}cos {120^o} =  – cos {60^o}\cot {135^o} =  – cot {45^o}end{array} right. Rightarrow left{ begin{array}{l}{cos ^2}{120^o} = {cos ^2}{60^o}\{cot ^2}{135^o} = {cot ^2}{45^o}end{array} right.)

( Rightarrow B = {sin ^2}{90^o} + {cos ^2}{60^o} + {cos ^2}{0^o} – {tan ^2}60 + {cot ^2}{45^o})

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

(left{ begin{array}{l}cos {0^o} = 1;;;cot {45^o} = 1;;;cos {60^o} = frac{1}{2}\tan {60^o} = sqrt 3 ;;;sin {90^o} = 1end{array} right.)

( Rightarrow B = {1^2} + {left( {frac{1}{2}} right)^2} + {1^2} – {left( {sqrt 3 } right)^2} + {1^2})

( Leftrightarrow B = 1 + frac{1}{4} + 1 – 3 + 1 = frac{1}{4}.)

c)

Đặt  (C = cos {60^o}.sin {30^o} + {cos ^2}{30^o})

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

(sin {30^o} = frac{1}{2};;;cos {30^o} = frac{{sqrt 3 }}{2};;cos {60^o} = frac{1}{2};)

( Rightarrow C = frac{1}{2}.frac{1}{2} + {left( {;frac{{sqrt 3 }}{2}} right)^2} = frac{1}{4} + frac{3}{4} = 1.)

<!–

Giải bài 3.2 trang 37 SGK Toán 10 Kết nối tri thức tập 1

<![CDATA[

Đơn giản các biểu thức sau:

a) (sin {100^o} + sin {80^o} + cos {16^o} + cos {164^o};)

b) (2sin left( {{{180}^o} – alpha } right).cot alpha  – cos left( {{{180}^o} – alpha } right).tan alpha .cot left( {{{180}^o} – alpha } right)) với ({0^o} < alpha  < {90^o}).

 

Giải bài 3.2 trang 37 SGK Toán 10 Kết nối tri thức tập 1

Đơn giản các biểu thức sau:

a) (sin {100^o} + sin {80^o} + cos {16^o} + cos {164^o};)

b) (2sin left( {{{180}^o} – alpha } right).cot alpha  – cos left( {{{180}^o} – alpha } right).tan alpha .cot left( {{{180}^o} – alpha } right)) với ({0^o} < alpha  < {90^o}).

Phương pháp giải

*Áp dụng công thức

Đối với hai góc bù nhau, (alpha ) và ({{{180}^0} – alpha }), ta có:

(begin{array}{l}
*sin left( {{{180}^0} – alpha } right) = sin alpha ;;;;;;;;;;;;;;;;;;;;;;;;;;;*cosleft( {{{180}^0} – alpha } right) =  – cosalpha \
*tan left( {{{180}^0} – alpha } right) =  – tan left( {x ne {{90}^0}} right);;;;;;;;;;*cot left( {{{180}^0} – alpha } right) =  – cot alpha left( {{0^0} < alpha  < {{180}^0}} right)
end{array})

Hướng dẫn giải

a) Ta có:  (left{ begin{array}{l}sin {100^o} = sin left( {{{180}^o} – {{80}^o}} right) = sin {80^o}\cos {164^o} = cos left( {{{180}^o} – {{16}^o}} right) =  – cos {16^o}end{array} right.)

( Rightarrow sin {100^o} + sin {80^o} + cos {16^o} + cos {164^o})( = sin {80^o} + sin {80^o} + cos {16^o} – cos {16^o})( = 2sin {80^o}.)

b) Ta có:

(left{ begin{array}{l}sin left( {{{180}^o} – alpha } right) = sin alpha \cos left( {{{180}^o} – alpha } right) =  – cos alpha \tan left( {{{180}^o} – alpha } right) =  – tan alpha \cot left( {{{180}^o} – alpha } right) =  – cot alpha end{array} right.quad ({0^o} < alpha  < {90^o}))( Rightarrow 2sin left( {{{180}^o} – alpha } right).cot alpha  – cos left( {{{180}^o} – alpha } right).tan alpha .cot left( {{{180}^o} – alpha } right)) ( = 2sin alpha .cot alpha  – left( { – cos alpha } right).tan alpha .left( { – cot alpha } right))( = 2sin alpha .cot alpha  – cos alpha .tan alpha .cot alpha )

adsense

( = 2sin alpha .frac{{cos alpha }}{{sin alpha }} – cos alpha .left( {tan alpha .cot alpha } right))( = 2cos alpha  – cos alpha  = cos alpha .)

<!–

Giải bài 3.3 trang 37 SGK Toán 10 Kết nối tri thức tập 1

<![CDATA[

Chứng minh các hệ thức sau:

a) ({sin ^2}alpha  + {cos ^2}alpha  = 1).

b) (1 + {tan ^2}alpha  = frac{1}{{{{cos }^2}alpha }}quad (alpha  ne {90^o}))

c) (1 + {cot ^2}alpha  = frac{1}{{{{sin }^2}alpha }}quad ({0^o} < alpha  < {180^o}))

 

Giải bài 3.3 trang 37 SGK Toán 10 Kết nối tri thức tập 1

Chứng minh các hệ thức sau:

a) ({sin ^2}alpha  + {cos ^2}alpha  = 1).

b) (1 + {tan ^2}alpha  = frac{1}{{{{cos }^2}alpha }}quad (alpha  ne {90^o}))

c) (1 + {cot ^2}alpha  = frac{1}{{{{sin }^2}alpha }}quad ({0^o} < alpha  < {180^o}))

Phương pháp giải

a)

Bước 1: Vẽ đường tròn lượng giác, lấy điểm M biểu diễn góc (alpha ) bất kì.

Bước 2: Xác định (sin alpha ,;cos alpha )( tương ứng với tung độ và hoành độ của điểm M).

Bước 3: Suy ra đẳng thức cần chứng minh.

b)

Bước 1: Viết (tan alpha ) dưới dạng (frac{{sin alpha }}{{cos alpha }};;(alpha  ne {90^o})), thay vào vế trái.

Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.

c)

Bước 1: Viết (cot alpha ) dưới dạng (frac{{cos alpha }}{{sin alpha }};), thay vào vế trái.

Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.

Hướng dẫn giải

a)

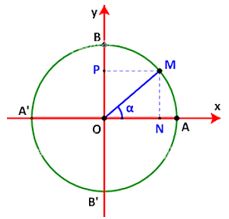
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho (widehat {xOM} = alpha ). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Ta có: (left{ begin{array}{l}x = cos alpha \y = sin alpha end{array} right. Rightarrow left{ begin{array}{l}{cos ^2}alpha  = {x^2}\{sin ^2}alpha  = {y^2}end{array} right.)(1)

Mà (left{ begin{array}{l}left| x right| = ON\left| y right| = OP = MNend{array} right. Rightarrow left{ begin{array}{l}{x^2} = {left| x right|^2} = O{N^2}\{y^2} = {left| y right|^2} = M{N^2}end{array} right.)(2)

Từ (1) và (2) suy ra ({sin ^2}alpha  + {cos ^2}alpha  = O{N^2} + M{N^2} = O{M^2}) (do (Delta OMN) vuông tại N)

( Rightarrow {sin ^2}alpha  + {cos ^2}alpha  = 1) (vì OM =1). (đpcm)

b) Ta có:  (tan alpha  = frac{{sin alpha }}{{cos alpha }};;(alpha  ne {90^o}))

( Rightarrow 1 + {tan ^2}alpha  = 1 + frac{{{{sin }^2}alpha }}{{{{cos }^2}alpha }} = frac{{{{cos }^2}alpha }}{{{{cos }^2}alpha }} + frac{{{{sin }^2}alpha }}{{{{cos }^2}alpha }} = frac{{{{sin }^2}alpha  + {{cos }^2}alpha }}{{{{cos }^2}alpha }})

Mà theo ý a) ta có ({sin ^2}alpha  + {cos ^2}alpha  = 1) với mọi góc (alpha )

( Rightarrow 1 + {tan ^2}alpha  = frac{1}{{{{cos }^2}alpha }}) (đpcm)

c) Ta có:  (cot alpha  = frac{{cos alpha }}{{sin alpha }};;;({0^o} < alpha  < {180^o}))

( Rightarrow 1 + {cot ^2}alpha  = 1 + frac{{{{cos }^2}alpha }}{{{{sin }^2}alpha }} = frac{{{{sin }^2}alpha }}{{{{sin }^2}alpha }} + frac{{{{cos }^2}alpha }}{{{{sin }^2}alpha }} = frac{{{{sin }^2}alpha  + {{cos }^2}alpha }}{{{{sin }^2}alpha }})

Mà theo ý a) ta có ({sin ^2}alpha  + {cos ^2}alpha  = 1) với mọi góc (alpha )

( Rightarrow 1 + {cot ^2}alpha  = frac{1}{{{{sin }^2}alpha }}) (đpcm)

<!–

Giải bài 3.4 trang 37 SGK Toán 10 Kết nối tri thức tập 1

<![CDATA[

Cho góc (alpha ;;({0^o} < alpha  < {180^o})) thỏa mãn (tan alpha  = 3)

Tính giá trị biểu thức: (P = frac{{2sin alpha  – 3cos alpha }}{{3sin alpha  + 2cos alpha }})

 

Giải bài 3.4 trang 37 SGK Toán 10 Kết nối tri thức tập 1

Cho góc (alpha ;;({0^o} < alpha  < {180^o})) thỏa mãn (tan alpha  = 3)

Tính giá trị biểu thức: (P = frac{{2sin alpha  – 3cos alpha }}{{3sin alpha  + 2cos alpha }})

Phương pháp giải

Chia cả tử và mẫu của P cho (cos alpha).

Hướng dẫn giải

Cách 1: 

Vì  (tan alpha  = 3) nên (cos alpha ne 0)

(begin{array}{l}
Rightarrow P = dfrac{{frac{{2sin alpha – 3cos alpha }}{{cos alpha }}}}{{frac{{3sin alpha + 2cos alpha }}{{cos alpha }}}} = dfrac{{2frac{{sin alpha }}{{cos alpha }} – 3}}{{3frac{{sin alpha }}{{cos alpha }} + 2}}\
Leftrightarrow P = dfrac{{2tan alpha – 3}}{{3tan alpha + 2}} = dfrac{{2.3 – 3}}{{3.3 + 2}} = dfrac{3}{{11}}.
end{array})

Cách 2: 

Ta có: (1 + {tan ^2}alpha  = frac{1}{{{{cos }^2}alpha }}quad (alpha  ne {90^o}))

( Rightarrow frac{1}{{{{cos }^2}alpha }} = 1 + {3^2} = 10)

( Leftrightarrow {cos ^2}alpha  = frac{1}{{10}} Leftrightarrow cos alpha  =  pm frac{{sqrt {10} }}{{10}})

Vì ({0^o} < alpha  < {180^o}) nên (sin alpha  > 0).

Mà (tan alpha  = 3 > 0 Rightarrow cos alpha  > 0 Rightarrow cos alpha  = frac{{sqrt {10} }}{{10}})

Lại có: (sin alpha  = cos alpha .tan alpha  = frac{{sqrt {10} }}{{10}}.3 = frac{{3sqrt {10} }}{{10}}.)

( Rightarrow P = dfrac{{2.frac{{3sqrt {10} }}{{10}} – 3.frac{{sqrt {10} }}{{10}}}}{{3.frac{{3sqrt {10} }}{{10}} + 2.frac{{sqrt {10} }}{{10}}}} = dfrac{{frac{{sqrt {10} }}{{10}}left( {2.3 – 3} right)}}{{frac{{sqrt {10} }}{{10}}left( {3.3 + 2} right)}} = dfrac{3}{{11}}.)