adsense
Giải bài tập Bài 9: Tích của một vectơ với một số (Kết nối)
==============
Giải bài 4.11 trang 50 SGK Toán 10 Kết nối tri thức tập 1
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị (overrightarrow {AM} ) theo hai vecto (overrightarrow {AB} ) và (overrightarrow {AD} ).
Phương pháp giải
Bước 1: Phân tích vecto (overrightarrow {AM} ) theo hai vecto cạnh.
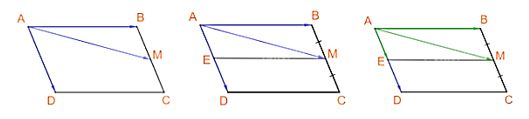
Bước 2: Biểu thị hai vecto cạnh theo vecto (overrightarrow {AB} ), (overrightarrow {AD} ).
Hướng dẫn giải
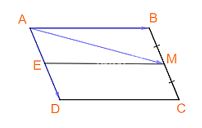
Từ M kẻ đường thẳng song song với AB, cắt AD tại E.
Khi đó tứ giác ABME là hình bình hành.
Do đó: (overrightarrow {AM} = overrightarrow {AB} + overrightarrow {AE} ).
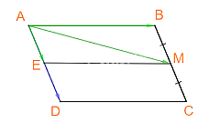
Dễ thấy: (AE = BM = frac{1}{2}BC = frac{1}{2}AD)
( Rightarrow overrightarrow {AE} = frac{1}{2}overrightarrow {AD} )
( Rightarrow overrightarrow {AM} = overrightarrow {AB} + frac{1}{2}overrightarrow {AD} )
Vậy (overrightarrow {AM} = overrightarrow {AB} + frac{1}{2}overrightarrow {AD} )
Giải bài 4.12 trang 50 SGK Toán 10 Kết nối tri thức tập 1
Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh (overrightarrow {BC} + overrightarrow {AD} = 2overrightarrow {MN} = ;overrightarrow {AC} + overrightarrow {BD} .)
Phương pháp giải
+ Với ba điểm A, B, C bất kì ta luôn có: (overrightarrow {AB} + overrightarrow {BC} = overrightarrow {AC} )
+ M là trung điểm của đoạn AB thì (overrightarrow {MA} + overrightarrow {MB} = overrightarrow 0 = overrightarrow {AM} + overrightarrow {BM} )
Hướng dẫn giải
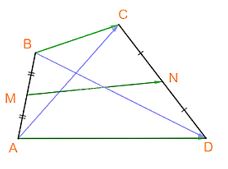
Ta có:
(overrightarrow {MN} = overrightarrow {MA} + overrightarrow {AD} + overrightarrow {DN} )
Mặt khác: (overrightarrow {MN} = overrightarrow {MB} + overrightarrow {BC} + overrightarrow {CN} )
(begin{array}{l} Rightarrow 2overrightarrow {MN} = overrightarrow {MA} + overrightarrow {AD} + overrightarrow {DN} + overrightarrow {MB} + overrightarrow {BC} + overrightarrow {CN} \ Leftrightarrow 2overrightarrow {MN} = left( {overrightarrow {MA} + overrightarrow {MB} } right) + left( {overrightarrow {DN} + overrightarrow {CN} } right) + overrightarrow {BC} + overrightarrow {AD} \ Leftrightarrow 2overrightarrow {MN} = overrightarrow 0 + overrightarrow 0 + overrightarrow {BC} + overrightarrow {AD} \ Leftrightarrow 2overrightarrow {MN} = overrightarrow {BC} + overrightarrow {AD} end{array})
Tương tự ta cũng có:
(left{ begin{array}{l}overrightarrow {MN} = overrightarrow {MA} + overrightarrow {AC} + overrightarrow {CN} \overrightarrow {MN} = overrightarrow {MB} + overrightarrow {BD} + overrightarrow {DN} end{array} right.)
(begin{array}{l} Rightarrow 2overrightarrow {MN} = overrightarrow {MA} + overrightarrow {AC} + overrightarrow {CN} + overrightarrow {MB} + overrightarrow {BD} + overrightarrow {DN} \ Leftrightarrow 2overrightarrow {MN} = left( {overrightarrow {MA} + overrightarrow {MB} } right) + left( {overrightarrow {CN} + overrightarrow {DN} } right) + overrightarrow {AC} + overrightarrow {BD} \ Leftrightarrow 2overrightarrow {MN} = overrightarrow 0 + overrightarrow 0 + overrightarrow {AC} + overrightarrow {BD} \ Leftrightarrow 2overrightarrow {MN} = overrightarrow {AC} + overrightarrow {BD} end{array})
Vậy (overrightarrow {BC} + overrightarrow {AD} = 2overrightarrow {MN} = ;overrightarrow {AC} + overrightarrow {BD} .)
Giải bài 4.13 trang 50 SGK Toán 10 Kết nối tri thức tập 1
Cho hai điểm phân biệt A và B.
a) Hãy xác định điểm K sao cho (overrightarrow {KA} + 2overrightarrow {KB} = overrightarrow 0 ).
b) Chứng minh rằng với mọi điểm O, ta có (overrightarrow {OK} = frac{1}{3}overrightarrow {OA} + frac{2}{3}overrightarrow {OB} .)
Phương pháp giải
Nhắc lại: Với ba điểm A, B, C bất kì ta luôn có: (overrightarrow {AB} + overrightarrow {BC} = overrightarrow {AC} )
a)
Cách 1: Nhận xét về phương chiều, độ lớn của hai vecto (overrightarrow {KA} ) và (;overrightarrow {KB} ), suy ra vị trí điểm K.
Cách 2: Biểu diễn vecto (overrightarrow {KA} ) hoặc (;overrightarrow {KB} )) theo vecto (;overrightarrow {AB} ).
b)
Biểu diễn vecto (overrightarrow {OK} ) bằng cách chèn điểm: (overrightarrow {OA} = overrightarrow {OK} + overrightarrow {KA} ;;,overrightarrow {OB} = overrightarrow {OK} + overrightarrow {KB} .)
Hướng dẫn giải
a)
Cách 1:
Ta có: (overrightarrow {KA} + 2overrightarrow {KB} = overrightarrow 0 ).
adsense
( Leftrightarrow overrightarrow {KA} = – 2overrightarrow {KB} )
Suy ra vecto (overrightarrow {KA} ) và vecto(;overrightarrow {KB} ) cùng phương, ngược chiều và (KA = 2.KB)
( Rightarrow K,A,B)thẳng hàng, K nằm giữa A và B thỏa mãn: (KA = 2.KB)
Cách 2:
Ta có: (overrightarrow {KA} + 2overrightarrow {KB} = overrightarrow 0 ).
(begin{array}{l} Leftrightarrow left( {overrightarrow {KB} + overrightarrow {BA} } right) + 2overrightarrow {KB} = overrightarrow 0 \ Leftrightarrow 3.overrightarrow {KB} + overrightarrow {BA} = overrightarrow 0 \ Leftrightarrow 3.overrightarrow {KB} = overrightarrow {AB} \ Leftrightarrow overrightarrow {KB} = frac{1}{3}overrightarrow {AB} end{array})
Vậy K thuộc đoạn AB sao cho (KB = frac{1}{3}AB).
b)
Để (overrightarrow {OK} = frac{1}{3}overrightarrow {OA} + frac{2}{3}overrightarrow {OB} .)
(begin{array}{l} Rightarrow overrightarrow {OK} = frac{1}{3}left( {overrightarrow {OK} + overrightarrow {KA} } right) + frac{2}{3}left( {overrightarrow {OK} + overrightarrow {KB} } right)\ Leftrightarrow overrightarrow {OK} = left( {frac{1}{3}overrightarrow {OK} + frac{2}{3}overrightarrow {OK} } right) + left( {frac{1}{3}overrightarrow {KA} + frac{2}{3}overrightarrow {KB} } right)\ Leftrightarrow overrightarrow {OK} = overrightarrow {OK} + frac{1}{3}left( {overrightarrow {KA} + 2overrightarrow {KB} } right)\ Leftrightarrow overrightarrow {OK} = overrightarrow {OK} + frac{1}{3}.overrightarrow 0 \ Leftrightarrow overrightarrow {OK} = overrightarrow {OK} .end{array})
Hiển nhiên đúng với mọi điểm O.
Vậy với mọi điểm O, ta có (overrightarrow {OK} = frac{1}{3}overrightarrow {OA} + frac{2}{3}overrightarrow {OB} .)
Chú ý khi giải:
Với những biểu thức đơn giản (chỉ có 3 điểm) thì từ giải thiết ta có thể suy ra ngay phương, chiều, độ dài của chúng để xác định điểm M.
Với các biểu thức phức tạp hơn (có nhiều hơn 3 điểm) thì nên sử dụng phương pháp như trên: quy về một vecto chưa biết, được biểu diễn qua các vecto đã biết.
Giải bài 4.14 trang 50 SGK Toán 10 Kết nối tri thức tập 1
Cho tam giác ABC
a) Hãy xác định điểm M để (overrightarrow {MA} + overrightarrow {MB} + 2overrightarrow {MC} = overrightarrow 0 )
b) Chứng minh rằng với mọi điểm O, ta có (overrightarrow {OA} + overrightarrow {OB} + 2overrightarrow {OC} = 4overrightarrow {OM} )
Phương pháp giải
Với ba điểm A, B, C bất kì ta luôn có: (overrightarrow {AB} + overrightarrow {BC} = overrightarrow {AC} )
Hướng dẫn giải
a) Ta có: (overrightarrow {MA} + overrightarrow {MB} + 2overrightarrow {MC} = overrightarrow 0 Leftrightarrow overrightarrow {MA} + left( {overrightarrow {MA} + overrightarrow {AB} } right) + 2left( {overrightarrow {MA} + overrightarrow {AC} } right) = overrightarrow 0 )
(begin{array}{l} Leftrightarrow overrightarrow {MA} + left( {overrightarrow {MA} + overrightarrow {AB} } right) + 2left( {overrightarrow {MA} + overrightarrow {AC} } right) = overrightarrow 0 \ Leftrightarrow 4overrightarrow {MA} + overrightarrow {AB} + 2overrightarrow {AC} = overrightarrow 0 \ Leftrightarrow 4overrightarrow {AM} = overrightarrow {AB} + 2overrightarrow {AC} \ Leftrightarrow overrightarrow {AM} = frac{1}{4}overrightarrow {AB} + frac{1}{2}overrightarrow {AC} end{array})
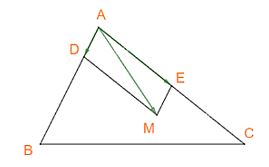
Trên cạnh AB, AC lấy điểm D, E sao cho (AD = frac{1}{4}AB;;,AE = frac{1}{2}AC)
Khi đó (overrightarrow {AM} = overrightarrow {AD} + overrightarrow {AE} ) hay M là đỉnh thứ tư của hình bình hành AEMD.
Giải bài 4.15 trang 59 SGK Toán 10 Kết nối tri thức tập 1
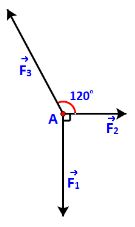
Chất điểm A chịu tác động của ba lực (overrightarrow {{F_1}} ,;overrightarrow {{F_2}} ,;overrightarrow {{F_3}} ) như hình 4.30 và ở trạng thái cân bằng (tức là (overrightarrow {{F_1}} + ;overrightarrow {{F_2}} + ;overrightarrow {{F_3}} = overrightarrow 0 )). Tính độ lớn của các lực (overrightarrow {{F_2}} ,;overrightarrow {{F_3}} ) biết (overrightarrow {{F_1}} ) có độ lớn là 20N.
Phương pháp giải
Bước 1: Xác định vecto (overrightarrow u = overrightarrow {{F_1}} + ;overrightarrow {{F_2}} ). Từ trạng thái của chất điểm suy ra mối liên hệ (phương, chiều, độ lớn) giữa (overrightarrow u ) và (overrightarrow {{F_3}} ).
Bước 2: Tính độ lớn của (overrightarrow {{F_2}} ,;overrightarrow {{F_3}} ).
Hướng dẫn giải
Bước 1: Đặt (overrightarrow u = overrightarrow {{F_1}} + ;overrightarrow {{F_2}} ). Ta xác định các điểm như hình dưới.
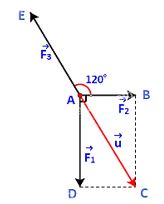
Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto (overrightarrow u ) chính là vecto (overrightarrow {AC} )
Vì chất điểm A ở trang thái cân bằng nên (overrightarrow {{F_1}} + ;overrightarrow {{F_2}} + ;overrightarrow {{F_3}} = overrightarrow 0 ) hay (;overrightarrow u + ;overrightarrow {{F_3}} = overrightarrow 0 )
( Leftrightarrow ;overrightarrow u ) và (;overrightarrow {{F_3}} ) là hai vecto đối nhau.
( Leftrightarrow A) là trung điểm của EC.
Bước 2:
Ta có: (left| {overrightarrow {{F_1}} } right| = AD = 20,;left| {overrightarrow {{F_2}} } right| = AB,;left| {overrightarrow {{F_3}} } right| = AC.)
Do A, C, E thẳng hàng nên (widehat {CAB} = {180^o} – widehat {EAB} = {60^o})
(begin{array}{l} Rightarrow widehat {CAD} = {90^o} – {60^o} = {30^o}\ Rightarrow left{ begin{array}{l}AC = frac{{AD}}{{cos {{30}^o}}} = frac{{40sqrt 3 }}{3};;\AB = DC = AC.sin {30^o} = frac{{20sqrt 3 }}{3}.end{array} right.end{array})
Vậy (;left| {overrightarrow {{F_2}} } right| = frac{{20sqrt 3 }}{3},;;left| {overrightarrow {{F_3}} } right| = frac{{40sqrt 3 }}{3}.)
