1. Giải bài 9.1 trang 23 SBT Vật lý 12
Một sóng ngang truyền dọc theo một sợi dây AB theo chiều từ A đến B. Đến đầu B của sợi dây thì sóng bị phản xạ trở lại.
Tại B, sóng phản xạ
A. luôn luôn ngược pha với sóng tới.
B. luôn luôn cùng pha với sóng tới.
C. ngược pha với sóng tới nếu đầu B được giữ cố định.
D. ngược pha với sóng tới nếu đầu B có thể di chuyển tự do.
Phương pháp giải
Để trả lời câu hỏi này cần nắm được các đặc điểm của sóng dừng
Hướng dẫn giải
– Trong sóng dừng:
+ Sóng phản xạ ngược pha sóng tới tại điểm phản xạ đối với sóng dừng hai đầu cố định.
+ Sóng phản xạ cùng pha sóng tới tại điểm phản xạ đối với sóng dừng một đầu cố định, một đầu tự do.
– Chọn C
2. Giải bài 9.2 trang 24 SBT Vật lý 12
Sóng dừng là
A. sóng không lan truyền được do bị một vật cản chặn lại.
B. sóng được tạo thành giữa hai điểm cố định trong một môi trường.
C. sóng được tạo thành do sự giao thoa giữa sóng tới và sóng phản xạ.
D. sóng được tạo thành do sự giao thoa của hai sóng kết hợp, trên đường thẳng nối giữa hai tâm phát sóng.
Phương pháp giải
Sự giao thoa giữa sóng tới và sóng phản xạ sẽ tạo thành sóng dừng
Hướng dẫn giải
– Sóng dừng là sóng được tạo thành do sự giao thoa giữa sóng tới và sóng phản xạ.
– Chọn C
3. Giải bài 9.3 trang 24 SBT Vật lý 12
Trong hệ sóng dừng trên một sợi dây mà hai đầu được giữ cố định thì bước sóng bằng
A. khoảng cách giữa hai nút hoặc hai bụng.
B. độ dài của dây.
C. hai lần độ dài của dây.
D. hai lần khoảng cách giữa hai nút hoặc hai bụng kề nhau.
Phương pháp giải
Khoảng cách giữa hai bụng (hai nút) liền kề bằng λ/2
Hướng dẫn giải
– Khoảng cách giữa hai bụng (hai nút) liền kề bằng λ/2
⇒ Bước sóng bằng hai lần khoảng cách giữa hai nút hoặc hai bụng kề nhau.
– Chọn D
4. Giải bài 9.4 trang 24 SBT Vật lý 12
Để tạo một hệ sóng dừng giữa hai đầu dây cố định thì độ dài của dây phải bằng
A. Một số nguyên lần bước sóng.
B. Một số nguyên lần nửa bước sóng.
C. Một số lẻ lần nửa bước sóng.
D. Một số lẻ lần bước sóng.
Phương pháp giải
Áp dụng điều kiện:
l = kλ/2
Hướng dẫn giải
– Điều kiện trên dây xảy ra sóng dừng hai đầu cố định:
l = k.λ/2
– Chọn B
5. Giải bài 9.5 trang 24 SBT Vật lý 12
Trong hệ sóng dừng trên một sợi dây, khoảng cách giữa hai nút liên tiếp bằng
A. Một bước sóng.
B. Nửa bước sóng.
C. Một phần tư bước sóng.
D. Hai lần bước sóng.
Phương pháp giải
Khoảng cách giữa hai bụng (hai nút) liền kề bằng λ/2
Hướng dẫn giải
– Trong hệ sóng dừng trên một sợi dây, khoảng cách giữa hai nút liên tiếp bằng nửa bước sóng
– Chọn B
6. Giải bài 9.6 trang 24 SBT Vật lý 12
Một sợi dây dài 1m hai đầu cố định và rung với hai múi thì bước sóng của dao động là
A. 1m B. 0,5m
C. 2m D. 0,25m
Phương pháp giải
Áp dụng công thức: l = kλ/2 (k nguyên)
để tìm bước sóng là: λ = 2l/k
Hướng dẫn giải
– Sóng dừng hai đầu cố định có hai múi sóng ⇒k=2
– Điều kiện trên dây xảy ra sóng dừng hai đầu cố định:
l = kλ/2 ⇒ λ = 2l/k = 2.1/2 = 1m
– Chọn A
7. Giải bài 9.7 trang 24 SBT Vật lý 12
Trên một sợi dây dài 90cm có sóng dừng. Kế cả hai nút ở hai đầu dây thì trên dây có 10 nút sóng. Biết tần số của sóng truyền trên dây là 200Hz. Sóng truyền trên dây có tốc độ là
A. 90cm/s B. 40m/s
C. 40cm/s D. 90m/s
Phương pháp giải
– Áp dụng công thức: l = kλ/2 (k nguyên)
để tìm bước sóng là: λ = 2l/k
– Công thức tính tốc độ truyền sóng: v=λf
Hướng dẫn giải
– Trên dây có 10 nút ⇒k=9
– Điều kiện trên dây xảy ra sóng dừng hai đầu cố định:
l = kλ/2 ⇒ λ = 2l/k = 2.90/9 = 20 cm
– Tốc độ truyền sóng:
v = λf = 20.200 = 4000cm/s =40m/s
– Chọn B
8. Giải bài 9.8 trang 25 SBT Vật lý 12
Sóng truyền trên một sợi dây có một đầu cố định, một đầu tự do. Muốn có sóng dừng trên dây thì chiều dài của sợi dây phải bằng
A. Một số lẻ lần nửa bước sóng.
B. Một số lẻ lần một phần tư bước sóng.
C. Một số nguyên lần bước sóng một đơn vị.
D. Một số chẵn lần một phần tư bước sóng.
Phương pháp giải
Áp dụng công thức:
l = (2m+1)λ/4 (m nguyên)
Hướng dẫn giải
– Điều kiện trên dây xảy ra sóng dừng một đầu cố định, một đầu tự do:
l = (2m+1).λ/4 (m nguyên)
– Chọn B
9. Giải bài 9.9 trang 25 SBT Vật lý 12
Trong sóng dừng trên dây, hiệu số pha của hai điểm trên dây nằm đối xứng qua một nút bằng
A. π/4(rad) B. π/2(rad)
C. π(rad) D. 0(rad)
Phương pháp giải
Sử dụng lí thuyết về sóng dừng
Hướng dẫn giải
– Hai điểm nằm trên hai múi liền kề dao động ngược pha nên độ lệch pha bằng π(rad)
– Chọn C
10. Giải bài 9.10 trang 25 SBT Vật lý 12
Một sóng dừng được hình thành trên một sợi dây căng ngang giữa hai điểm cố định. Trên sợi dây đó ta thấy:
A. Số bụng sóng nhiều hơn số nút sóng.
B. Số bụng sóng bằng số nút sóng.
C. Số bụng sóng ít hớn số nút sóng một đơn vị.
D. Số bụng sóng ít hơn số nút sóng hai đơn vị.
Phương pháp giải
Sóng dừng hai đầu cố định: số bụng sóng ít hơn số nút sóng một đơn vị
Hướng dẫn giải
– Một sóng dừng được hình thành trên một sợi dây căng ngang giữa hai điểm cố định.
– Trên sợi dây đó ta thấy số bụng sóng ít hơn số nút sóng một đơn vị.
– Chọn C
11. Giải bài 9.11 trang 25 SBT Vật lý 12
Một sợi dây dài L được giữ chặt một đầu, còn đầu kia là nguồn dao động với biên độ nhỏ.
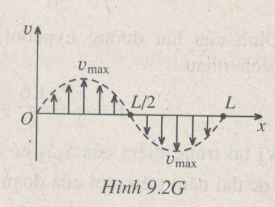
a) Người ta quan sát thấy trên dây xuất hiện hai bụng và một nút (trừ hai đầu dây). Tính bước sóng λ.
b) Tại thời điểm mà dây được trông thấy là thẳng thì vận tốc tức thời của các điểm trên dây sẽ như thế nào? Hãy vẽ hình miêu tả sự phân bố các vận tốc đó.
Phương pháp giải
Áp dụng công thức: l = kλ/2 (k nguyên)
để tính bước sóng là: λ = 2L/k
Hướng dẫn giải
a) Trên dây có hai bụng sóng ⇒k=2
Điều kiện trên dây xảy ra sóng dừng hai đầu cố định:
L = kλ/2 ⇒ λ = 2L/2 =L
b) Vận tốc của các điểm trên dây phụ thuộc vị trí từng điểm. Hai điểm của dây ở cách đều một nút về hai phía luôn dao động ngược pha nhau. Khi đi qua vị trí cân bằng, các điểm có tốc độ lớn nhất
12. Giải bài 9.12 trang 25 SBT Vật lý 12
Một dải lụa có độ dài l=1,05m một đầu gắn vào một cần rung R, rồi buông thõng theo phương thẳng đứng. Cần R được kích thích bằng một nam châm điện nuôi bằng một dòng điện xoay chiều mà tần số f có thể thay đổi được một cách dễ dàng. Khi được kích thích, thì cần rung rung với tần số gấp hai lần tần số dòng điện.
a) Đầu dưới của dải lụa được thả tự do. Khi tần số dòng điện là 0,75Hz thì dải lụa dao động ổn định với hai nút, mà một nút có thể coi như ở chỗ dải lụa gắn vào cần R. Cho tần số dòng điện tăng dần. Hỏi với các tần số f1,f2,f3 bằng bao nhiêu thì trên dải lụa lại xuất hiện thêm 1,2 và 3 nút nữa?
b) Đầu dưới của dải lụa bây giờ được giữ cố định. Giả sử tốc độ truyền sóng trên dải lụa không thay đổi, để xuất hiện một nút ở trung điểm dải lụa thì tần số dòng điện phải bằng bao nhiêu?
Phương pháp giải
a) Theo đề bài, xác định được bước sóng là: λ =4/3l
– Tốc độ truyền sóng được tính theo công thức: v = λf
⇒ công thức tính tần số: f=v/λ
– Khi trên dây có 1 nút và thêm 2 nút
⇒ công thức tần số dòng điện: f2′ = 1/2f2
b) Sử dụng công thức: λ=I/k để tính bước sóng và công thức tính tần số: f=v/λ
Hướng dẫn giải
a) Đầu dưới của một dải lụa được tự do, vậy tại đó có một bụng sóng, ở đầu kia có một nút, trên dây còn có một nút nữa vậy độ dài dây:
l = 3/4λ ⇒ λ =4/3l = 4/3.1,05 = 1,4m
Tốc độ truyền sóng trên dây là:
v = λf = 1,4.2.0,75 = 2,1m/s
– Trên dây thêm một nút thì:
\(\begin{array}{*{20}{l}} {l = \frac{5}{4}{\lambda _1}}\\ { \Rightarrow {\lambda _1} = \frac{4}{5}l = \frac{4}{5}.1,05 = 0,84m}\\ { \Rightarrow {f_1} = \frac{v}{{{\lambda _1}}} = \frac{{2,1}}{{0,84}} = 2,5Hz} \end{array}\)
⇒ Tần số dòng điện:
f1′ = 1/2f1 = 1/2.2,5 = 1,25 Hz
– Trên dây thêm hai nút thì:
\(\begin{array}{*{20}{l}} {l = \frac{7}{4}{\lambda _2}}\\ { \Rightarrow {\lambda _2} = \frac{4}{7}l = \frac{4}{5}.1,05 = 0,6m}\\ { \Rightarrow {f_2} = \frac{v}{{{\lambda _2}}} = \frac{{2,1}}{{0,6}} = 3,5Hz} \end{array}\)
⇒ Tần số dòng điện:
f2′ = 1/2f2 = 1/2.3,5 = 1,75Hz
– Trên dây thêm ba nút thì:
\(\begin{array}{*{20}{l}} {l = \frac{9}{4}{\lambda _3}}\\ { \Rightarrow {\lambda _3} = \frac{4}{9}l = \frac{4}{9}.1,05 = 0,47m}\\ { \Rightarrow {f_3} = \frac{v}{{{\lambda _3}}} = \frac{{2,1}}{{0,47}} = 4,5Hz} \end{array}\)
⇒ Tần số dòng điện:
f3′ = 1/2 f3 = 1/2.4,5 = 2,25Hz
b) Đầu dưới dưới được giữ cố định, khi đó có một nút dao động. Để tại trung điểm dải lụa có một nút dao động thì dải lụa phải chứa một số chẵn lần nửa bước sóng, tức là số nguyên lần nửa bước sóng.
Ta có: l = kλ ⇒ λ = l/k (k=1,2,3…)
– Gọi tần số dao động là fk tương ứng với tần số dòng điện là: fk′
\(\begin{array}{l} {f_k} = \frac{v}{{{\lambda _k}}} = k.\frac{v}{l} = k.\frac{{2,1}}{{1,05}} = 2k(Hz)\\ {f_k}^\prime = \frac{1}{2}{f_k} = k(Hz) \end{array}\)
13. Giải bài 9.13 trang 26 SBT Vật lý 12
Đế chứng minh sự cộng hưởng âm, người ta thường làm thí nghiệm như Hình 9.1. T là một ống nghiệm cao, A là một âm thoa có tần số dao động riêng f. Gõ cho âm thoa rung, thì nó phát ra một âm rất yếu. Đưa âm thoa lại gần miệng ống nghiệm, rồi đổ dần nước vào ống cho mực nước cao dần thì có thể tìm được độ cao hh của cột không khí trong ống, để cột không khí dao động cộng hưởng với âm thoa. Lúc đó âm được khuếch đại rất mạnh.
Cho biết: f=850Hz, h=50cm. Tính tốc độ v của âm.
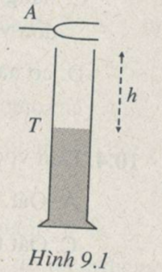
Phương pháp giải
– Sử dụng điều kiện trên dây xảy ra sóng dừng một đầu cố định, một đầu tự do:
l = (2m+1).λ/4 (m nguyên)
– Công thức tính tốc độ truyền sóng: v = λf
Hướng dẫn giải
– Khi hệ sóng dừng ổn định, miệng ống có một bụng sóng, đáy ống tức là mặt nước có một nút.
Vậy độ cao h phải thỏa mãn điều kiện:
h = (2m+1).λ/4 (m nguyên)
\(\begin{array}{l} \Rightarrow \lambda = \frac{{4h}}{{2m + 1}}\\ v = \lambda f = \frac{{4hf}}{{2m + 1}} = \frac{{4.0,5.850}}{{2m + 1}} \end{array}\)
– Tốc độ âm trong không khí cỡ 300m/s
⇒ v = 340 m/s
14. Giải bài 9.14 trang 26 SBT Vật lý 12
Một lò xo ống dài 1,2m có đầu trên gắn vào một nhánh âm thoa, đầu dưới treo một quả cân. Dao động của âm thoa được duy trì bằng một nam châm điện, và có tần số 50Hz. Khi đó, trên dây có một hệ sóng dừng, và trên lò xo chỉ có một nhóm vòng dao động với biên độ cực đại. Tính tốc độ truyền sóng trên lò xo.
Phương pháp giải
– Từ công thức: l = kλ/2 (k nguyên)
tính được bước sóng theo công thức là: λ = 2l/k
– Áp dụng công thức: v=λf để tính tốc độ truyền sóng
Hướng dẫn giải
– Trên lò xo có một bụng ⇒k=1
– Bứớc sóng là:
l = kλ/2 ⇒ λ = 2l/k = 2.1,2/1= 2,4 m
– Tốc độ truyền sóng:
v = λf = 2,4.50 = 120 m/s
==== GIAIBT.COM ====
