adsense
GIẢI SGK Bài 5. Phương trình lượng giác cơ bản – Toán 11 CTST
==============
Bài 1 trang 40 SGK Toán 11 tập 1 – CTST
Đề bài
Giải các phương trình lượng giác sau:
\(\begin{array}{l}a,\,\,sin2x = \;\frac{1}{2}\\b)\;sin(x – \frac{\pi }{7}) = sin\frac{{2\pi }}{7}\\c)\;sin4x – cos\left( {x + \frac{\pi }{6}} \right) = 0\end{array}\)
Phương trình sinx = m ,
-
- Nếu \(\left| m \right| \le 1\) thì phương trình vô nghiệm.
-
- Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm:
Khi đó, tồn tại duy nhất \(\alpha \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\) thoả mãn \(\sin \alpha = m\),
\({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi – \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết
a) Vì \(\sin \frac{\pi }{6} = \frac{1}{2}\) nên ta có phương trình \(sin2x = \sin \frac{\pi }{6}\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{6} + k2\pi \\2x = \pi – \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k\pi \\x = \frac{{5\pi }}{{12}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\(\begin{array}{l}b,\,\,sin(x – \frac{\pi }{7}) = sin\frac{{2\pi }}{7}\\ \Leftrightarrow \left[ \begin{array}{l}x – \frac{\pi }{7} = \frac{{2\pi }}{7} + k2\pi \\x – \frac{\pi }{7} = \pi – \frac{{2\pi }}{7} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\pi }}{7} + k2\pi \\x = \frac{{6\pi }}{7} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}\;c)\;sin4x – cos\left( {x + \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow sin4x = cos\left( {x + \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{2} – x – \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{3} – x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{\pi }{3} – x + k2\pi \\4x = \pi – \frac{\pi }{3} + x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{15}} + k\frac{{2\pi }}{5}\\x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Bài 2 trang 40 SGK Toán 11 tập 1 – CTST
Đề bài
Giải các phương trình lượng giác sau:
\(\begin{array}{l}a)\;\,cos(x + \frac{\pi }{3}) = \frac{{\sqrt 3 }}{2}\\b)\;\,cos4x = cos\frac{{5\pi }}{{12}}\\c)\;\,co{s^2}x = 1\end{array}\)
Phương trình \({\rm{cosx}} = m\),
-
- Nếu \(\left| m \right| \le 1\) thì phương trình vô nghiệm.
-
- Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm:
Khi \(\left| m \right| \le 1\)sẽ tồn tại duy nhất \(\alpha \in \left[ {0;\pi } \right]\) thoả mãn \({\rm{cos}}\alpha = m\). Khi đó:
\({\rm{cosx}} = m \Leftrightarrow {\rm{cosx}} = {\rm{cos}}\alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = – \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết
\(\begin{array}{l}a)\;\,cos(x + \frac{\pi }{3}) = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow cos\left( {x + \frac{\pi }{3}} \right) = cos\frac{\pi }{6}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{3} = \frac{\pi }{6} + k2\pi \\x + \frac{\pi }{3} = -\frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = -\frac{\pi }{6} + k2\pi \\x = -\frac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}b)\;\,cos4x = cos\frac{{5\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{{5\pi }}{{12}} + k2\pi \\4x = -\frac{{5\pi }}{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{{48}} + k\frac{\pi }{2}\\x = -\frac{{5\pi }}{{48}} + k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}c)\;\,co{s^2}x = 1\\ \Leftrightarrow \left[ \begin{array}{l}cosx = 1\\cosx = -1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \pi + k2\pi \end{array} \right. \Leftrightarrow x = k\pi ,k \in \mathbb{Z}\end{array}\)
Bài 3 trang 41 SGK Toán 11 tập 1 – CTST
Đề bài
Giải các phương trình lượng giác sau:
\(\begin{array}{l}a){\rm{ }}tanx = tan55^\circ ;\\b,\,\tan \left( {2x + \frac{\pi }{4}} \right) = 0\end{array}\)
Phương trình \(\tan x = m\)có nghiệm với mọi m.
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)\) thoả mãn \(\tan \alpha = m\). Khi đó:
\(\tan {\rm{x}} = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
Lời giải chi tiết
a, Điều kiện xác định: \(x \ne 90^\circ + k180^\circ \).
Ta có:\({\rm{ }}tanx = tan55^\circ \Leftrightarrow x = 55^\circ + k180^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}\,\,(TM).\)
b, Điều kiện xác định: \(2x + \frac{\pi }{4} \ne \frac{\pi }{2} + k\pi \Leftrightarrow x \ne \frac{\pi }{8} + k\pi ,k \in \mathbb{Z}.\)
Ta có: \(\tan \left( {2x + \frac{\pi }{4}} \right) = 0 \Leftrightarrow 2x + \frac{\pi }{4} = k\pi \Leftrightarrow x = -\frac{\pi }{8} + k\frac{\pi }{2},k \in \mathbb{Z}\,\,(TM).\)
Bài 4 trang 41 SGK Toán 11 tập 1 – CTST
Đề bài
Giải các phương trình lượng giác sau:
\(\begin{array}{l}a)\;cot\left( {\frac{1}{2}x + \frac{\pi }{4}} \right) = – 1\\b)\;cot3x = – \frac{{\sqrt 3 }}{3}\end{array}\)
Phương trình \(\cot x = m\)có nghiệm với mọi m.
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( {0;\pi } \right)\) thoả mãn \(\cot \alpha = m\). Khi đó:
\(\cot {\rm{x}} = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
Lời giải chi tiết
a, Điều kiện xác định: \(\frac{1}{2}x + \frac{\pi }{4} \ne k\pi \Leftrightarrow x \ne – \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\)
adsense
Ta có: \(cot\left( {\frac{1}{2}x + \frac{\pi }{4}} \right) = – 1 \Leftrightarrow cot\left( {\frac{1}{2}x + \frac{\pi }{4}} \right) = \cot \left( { – \frac{\pi }{4}} \right)\)
\( \Leftrightarrow \frac{1}{2}x + \frac{\pi }{4} = – \frac{\pi }{4} + k\pi \Leftrightarrow x = – \pi + k2\pi ,k \in \mathbb{Z}\,\,(TM).\)
Vậy \(x = – \pi + k2\pi ,k \in \mathbb{Z}\,\).
b, Điều kiện xác định: \(3x \ne k\pi \Leftrightarrow x \ne k\frac{\pi }{3},k \in \mathbb{Z}.\)
\(\;cot3x = – \frac{{\sqrt 3 }}{3} \Leftrightarrow cot3x = \cot \left( { – \frac{\pi }{3}} \right)\)
\( \Leftrightarrow 3x = – \frac{\pi }{3} + k\pi \Leftrightarrow x = – \frac{\pi }{9} + k\frac{\pi }{3},k \in \mathbb{Z}\,\,(TM).\)
Vậy \(x = – \frac{\pi }{9} + k\frac{\pi }{3},k \in \mathbb{Z}\,\).
Bài 5 trang 41 SGK Toán 11 tập 1 – CTST
Đề bài
Tại các giá trị nào của x thì đồ thị hàm số y = cosx và y = sinx giao nhau?
Sử dụng công thức \(\sin x = cos\left( {\frac{\pi }{2} – x} \right)\) và giải phương trình côsin
Lời giải chi tiết
Đồ thị hàm số y = cosx và y = sinx giao nhau tại điểm x thoả mãn
\(cosx = sinx \Leftrightarrow cosx = cos\left( {\frac{\pi }{2} – x} \right)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} – x + k2\pi \\x = – \frac{\pi }{2} + x + k2\pi \end{array} \right. \Leftrightarrow x = \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}.\)
Vậy \(x = \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}.\)
Bài 6 trang 41 SGK Toán 11 tập 1 – CTST
Đề bài
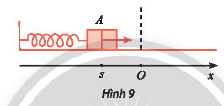
Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Toạ độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức \(s = 10sin\left( {10t + \frac{\pi }{2}} \right).\)Vào các thời điểm nào thì \(s = – 5\sqrt 3 \;\)cm?
Phương trình sinx = m ,
-
- Nếu \(\left| m \right| \le 1\) thì phương trình vô nghiệm.
-
- Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm:
Khi đó, tồn tại duy nhất \(\alpha \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\) thoả mãn \(\sin \alpha = m\),
\({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \) \( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi – \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết
Khi: \(s = – 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = – 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = – \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { – \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = – \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = – \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.
Bài 7 trang 41 SGK Toán 11 tập 1 – CTST
Đề bài
Trong Hình 10, ngọn đèn trên hải đăng H cách bờ biển yy’ một khoảng HO = 1 km. Đèn xoay ngược chiều kim đồng hồ với tốc độ \(\frac{\pi }{{10}}\)rad/s và chiếu hai luồng ánh sáng về phía đối diện nhau. Khi đèn xoay, điểm M mà luồng ánh sáng của hải đăng rọi vào bờ biển chuyển dộng dọc theo bờ.
(Theo https://www.mnhs.org/splitrock/learn/technology)

a) Ban đầu luồng sáng trùng với đường thẳng HO. Viết hàm số biểu thị toạ độ \({y_M}\) của điệm M trên trục Oy theo thời gian t
b) Ngôi nhà N nằm trên bờ biển với toạ độ \({y_N} = – 1\;\left( {km} \right).\)Xác định các thời điểm t mà đèn hải đăng chiếu vào ngôi nhà.
a, Dựa vào đề bài để viết hàm số biểu thị toạ độ \({y_M}\) .
b, Phương trình \(\tan x = m\)có nghiệm với mọi m.
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)\) thoả mãn \(\tan \alpha = m\). Khi đó:
\(\tan {\rm{x}} = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
Lời giải chi tiết
a) Sau t giây điểm M quét được một góc lượng giác có số đo là: \(\alpha = \frac{\pi }{{10}}t\) rad.
Xét tam giác HOM vuông tại O có:
\(MO = tan\alpha .1 = \tan \left( {\frac{\pi }{{10}}t} \right)\).
Vậy tọa độ \({y_M} = \tan \left( {\frac{\pi }{{10}}t} \right)\).
b) Xét \(\tan \left( {\frac{\pi }{{10}}t} \right) = – 1\)
\(\begin{array}{l} \Leftrightarrow \tan \left( {\frac{\pi }{{10}}t} \right) = \tan \left( { – \frac{\pi }{4}} \right)\\ \Leftrightarrow \frac{\pi }{{10}}t = – \frac{\pi }{4} + k\pi \\ \Leftrightarrow t = – \frac{5}{2} + 10k,k \in \mathbb{Z}.\end{array}\)
Vì \(t \ge 0\) nên tại các thời điểm \(t = – \frac{5}{2} + 10k,k \in \mathbb{Z},k \ge 1\) thì đèn hải đăng chiếu vào ngôi nhà.
