I. Lý thuyết dao động điều hòa
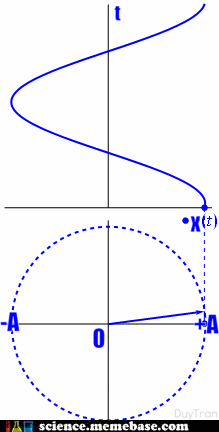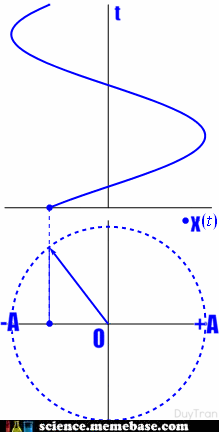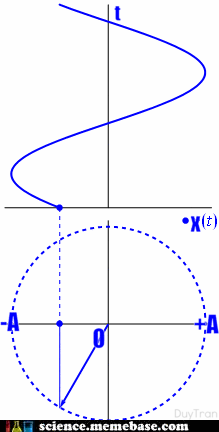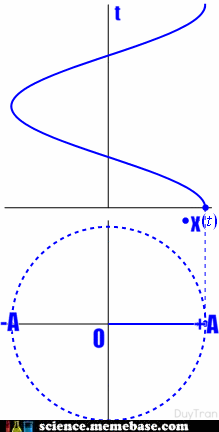
– Định nghĩa: Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.
– Phương trình dao động điều hòa: (x = Acos left( {omega t + varphi } right))
Trong đó:
+ x: li độ của dao động
+ A: biên độ dao động
+ (omega ): tần số góc của dao động (đơn vị rad/s)
+ (omega t + varphi ): pha của dao động tại thời điểm t
+ (varphi ): pha ban đầu của dao động
– Phương trình vận tốc: (v = x’ = omega Acos left( {omega t + varphi + frac{pi }{2}} right))
+ Tại VTCB vận tốc có độ lớ cực đại ({v_{max }} = omega A)
+ Tại biên vận tốc bằng 0
+ Vận tốc nhanh pha hơn li độ một góc (frac{pi }{2}) và vận tốc đổi chiều tại biên độ.
– Phương trình gia tốc: (a = v’ = {omega ^2}Acos left( {omega t + varphi + pi } right))
+ Vectơ gia tóc luôn luôn hướng về vị trí cân bằng
+ Tại biên gia tốc có độ lớn cực đại ({a_{max }} = {omega ^2}A), tại VTCB gia tốc bằng 0
+ Gia tốc nhanh pha hơn vận tốc một góc (frac{pi }{2}) và ngược pha với li độ.
II. Các đại lượng đặc trưng của dao động điều hòa
– Chu kì T (s): là khoảng thời gian để vật thực hiện được một dao động toàn phần:
(T = dfrac{{2pi }}{omega } = dfrac{{Delta t}}{N}) với N là tổng số dao động trong thời gian (Delta t)
– Tần số f (Hz): là số dao động toàn phần thực hiện được trong 1 giây
(f = dfrac{omega }{{2pi }} = dfrac{1}{T})
– Tần số góc (omega ) (rad/s): là đại lượng liên hệ với chu kì T hay tần số f bằng hệ thức:
(omega = frac{{2pi }}{T} = 2pi f)
– Biên độ dao động A: là độ lệch lớn nhất của vật dao động so với vị trí cân bằng của nó.
({A^2} = {x^2} + dfrac{{{v^2}}}{{{omega ^2}}} = dfrac{{{a^2}}}{{{omega ^4}}} + dfrac{{{v^2}}}{{{omega ^2}}})
(A = dfrac{{{v_{max }}}}{omega } = dfrac{{{a_{max }}}}{{{omega ^2}}} = dfrac{L}{2} = dfrac{S}{4} = dfrac{{v_{max }^2}}{{{a_{max }}}})
Trong đó:
+ L là chiều dài quỹ đạo chuyển động của vật: L = 2A
+ S là quãng đường vật đi được trong một chu kì: S = 4A
