Tìm nhanh giao tuyến giữa 2 mặt phẳng trong không gian – bài tập có đáp án
Phương pháp giải xác định giao tuyến giữa 2 mp
Để xác định giao tuyến của hai mặt phẳng, ta đi tìm hai điểm chung của chúng. Đường thẳng đi qua hai điểm chung đó là giao tuyến.
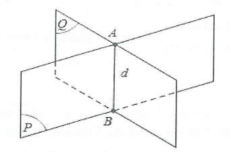
Lưu ý: Điểm chung của hai mặt phẳng (P) và (Q) thường được tìm như sau:
Tìm hai đường thẳng a và b lần lượt thuộc mặt phẳng (P) và (Q) cùng nằm trong một mặt phẳng (R). Giao điểm $M=acap b$ chính là điểm chung của mặt phẳng (P) và (Q).
Bài tập trắc nghiệm tình giao tuyến giữa hai mặt phẳng
| Bài tập 1: Cho hình chóp S.ABCD, có đáy ABCD là tứ giác có cặp cạnh đối diện không song song, điểm M thuộc cạnh SA. Tìm giao tuyến của các cặp mặt phẳng sau:
A. (SAC) và (SBD) B. (SAC) và (MBD) C. (MBC) và (SAD) D. (SAB) và (SCD) |
Lời giải chi tiết
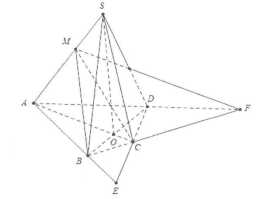
a) Trong mặt phẳng (ABCD) gọi $O=ACcap BDRightarrow left{ begin{array} {} Oin ACsubset left( SAC right) \ {} Oin BDsubset left( SBD right) \ end{array} right.$ .
Khi đó hai mặt phẳng (SAC) và (SBD) có hai điểm chung là S và O$Rightarrow SO=left( SAC right)cap left( SBD right).$
b) Điểm $Min SARightarrow Min left( SAC right).$
Hai mặt phẳng (SAC) và (MBD) có hai điểm chung là O và M nên $OM=left( SAC right)cap left( MBD right).$
c) Gọi $F=ADcap BC$ suy ra $left{ begin{array} {} Fin left( MBC right) \ {} Fin left( SAD right) \ end{array} right..$ Khi đó hai mặt phẳng (MBC) và (SAD) có hai điểm chung là M và F $Rightarrow MF=left( MBC right)cap left( SAD right)$ .
d) Gọi $E=ABcap CD$ suy ra $left{ begin{array} {} Ein left( SAB right) \ {} Ein left( SCD right) \ end{array} right.Rightarrow $ hai mặt phẳng (SAB) và (SCD) có hai điểm chung là S và E $Rightarrow SE=left( SAB right)cap left( SCD right)$ .
| Bài tập 2: Cho hình chóp S.ABC và điểm I thuộc đoạn SA. Một đường thẳng không song song với mặt cắt các cạnh AB và BC lần lượt tại J và K. Tìm giao tuyến của các cặp mặt phẳng sau:
A. Mặt phẳng (IJK) và (SAC) B. Mặt phẳng (IJK) và (SAB) C. Mặt phẳng (IJK) và (SBC) |
Lời giải chi tiết
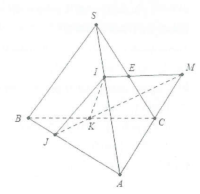
a) Trong mặt phẳng (ABC) gọi $M=JKcap AC$ .
Khi đó 2 mặt phẳng (IJK) và (SAC) có hai điểm chung là I và M.
Suy ra $IM=left( text{IJ}K right)cap left( SAC right)$ .
b) Hai mặt phẳng (IJK) và (SAB) có hai điểm chung là I và J $Rightarrow text{IJ}=left( text{IJ}K right)cap left( SAB right)$ .
c) Trong mặt phẳng (SAC) gọi $E=SCcap IM$ .
Khi đó $left{ begin{array} {} Ein left( text{IJ}K right) \ {} Ein left( SBC right) \ end{array} right.Rightarrow $hai mặt phẳng (IJK) và (SBC) có hai điểm chung là E và K. Do đó $KE=left( text{IJ}K right)cap left( SBC right)$
| Bài tập 3: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (JAD) b) Điểm M nằm trên cạnh AB, điểm N nằm trên cạnh AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN). |
Lời giải chi tiết
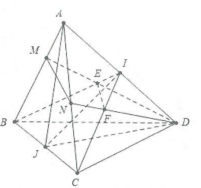
a) Ta có: $Iin ADRightarrow Iin left( JAD right)cap left( IBC right)$
$Jin BCRightarrow Jin left( JAD right)cap left( IBC right).$
Do đó $text{IJ}=left( IBC right)cap left( JAD right)$
b) Trong mặt phẳng (ABC) gọi $E=DMcap IB$
suy ra $Ein left( DMN right)cap left( IBC right)$
Do đó $text{EF}=left( DMN right)cap left( IBC right)$
| Bài tập 4: Cho tứ diện ABCD. Điểm M nằm bên trong tam giác ABD, điểm N nằm bên trong tam giác ACD. Tìm giao tuyến của các cặp mặt phẳng sau:
a) (AMN) và (BCD). b) (DMN) và (ABC). |
Lời giải chi tiết
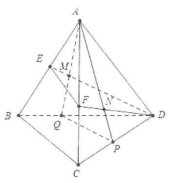
a) Trong mặt phẳng (ABD) gọi $Q=AMcap BD$
Khi đó $Qin left( AMN right)cap left( BCD right)$
Tương tự gọi $P=ANcap CDRightarrow P=left( AMN right)cap left( BCD right)$
Do vậy $PQ=left( AMN right)cap left( BCD right).$
b) Trong mặt phẳng (ABD) gọi $E=DMcap AB$ suy ra $Ein left( DMN right)cap left( ABC right)$ .
Trong mặt phẳng (ACD) gọi $F=DNcap AC$ suy ra $Fin left( DMN right)cap (ABC).$
Do đó $text{EF}=left( DMN right)cap left( ABC right)$
| Bài tập 5: Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành tâm O, gọi M, N, P lần lượt là trung điểm của BC, CD và SO. Tìm giao tuyến của
a) Mặt phẳng (MNP) và (SAB). b) Mặt phẳng (MNP) và (SBC). |
Lời giải chi tiết
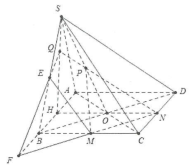
a) Gọi $H=NOcap AB,$ trong mặt phẳng (SHN) dựng NP cắt SH tại $QRightarrow Qcap left( MNP right)cap left( SAB right).$
Gọi $F=NMcap ABRightarrow Fin left( MNP right)cap left( SAB right).$ Do đó $QF=left( SAB right)cap left( MNP right)$
b) Trong mặt phẳng (SAB). Gọi $E=QFcap SBRightarrow E=left( SBC right)cap left( MNP right)$
Do đó $ME=left( MNP right)cap left( SBC right).$
| Bài tập 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I và J lần lượt là trung điểm của SA và SB. Khẳng định nào sau đây sai?
A. IJCD là hình thang B. $left( SAB right)cap left( IBC right)=IB$ C. $left( SBD right)cap left( JCD right)=JD$ D. $left( IAC right)cap left( IBD right)=AO,$ (O là tâm ABCD) |
Lời giải chi tiết
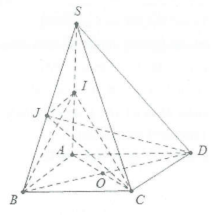
Ta có $left{ begin{array} {} text{IJ}parallel AB \ {} ABparallel CD \ end{array} right.Rightarrow text{IJ}parallel CDRightarrow $Loại A
+) $left( SAB right)cap left( IBC right)=IBRightarrow $Loại B
+) $left( SBD right)cap left( JCD right)=JDRightarrow $ Loại C
+) $left( IAC right)cap left( JBD right)=left( SAC right)cap left( SBD right)=SO.$ Chọn D.
| Bài tập 7: Cho hình chóp S.ABCD có đáy là hình thang ABCD (AD//BC). Gọi M là trung điểm của CD. Giao tuyến của hai mặt phẳng (MSB) và (SAC) là:
A. SI, I là giao điểm của AC và BM B. SJ (J là giao điểm của AM và BD). C. SO (O là giao điểm của AC và BD) D. SP (P là giao điểm của AB và CD) |
Lời giải chi tiết
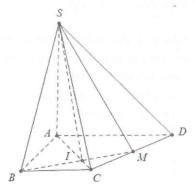
Ta có: $left( MSB right)cap left( SAC right)=SI.$ Chọn A
| Bài tập 8: Cho hình tứ diện ABCD, trên các cạnh AB và AC lấy các điểm M và N sao cho MN cắt đường thẳng BC tại E, điểm P thuộc cạnh BD. Gọi Q là giao điểm của CD và PE. Khẳng định nào sau đây là sai:
A. $left( MNP right)cap left( BCD right)=PE$ B. $left( MNP right)cap left( ABD right)=MP$ C. $left( MNP right)cap left( ABC right)=MN$ D. $left( MNP right)cap left( ACD right)=PN$ |
Lời giải chi tiết
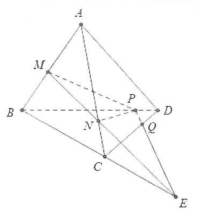
Ta có: $Ein MNRightarrow Ein left( MNP right)$
Khi đó (MNP) và (BCD) có 2 điểm chung là P và E
Do đó $left( MNP right)cap (BCD)=PE.$
Điểm M, P$in left( ABD right)$ suy ra $left( MNP right)cap left( ABD right)=MP$
Điểm $M,Nin left( ABC right)$ suy ra $left( MNP right)cap left( ABC right)=MN.$
$left( MNP right)cap left( ACD right)=NQ.$
Khẳng định sai là D. Chọn D.
| Bài tập 9: Cho hình tứ diện ABCD, trên các cạnh AB, AC và AD lần lượt lấy các điểm M, N và P. Đường thẳng MN và BC cắt nhau tại E, đường thẳng MP và BD cắt nhau tại F. Khẳng định nào sau đây là sai.
A. $left( MNP right)cap left( ABC right)=ME$ B. $left( MNP right)cap left( ABD right)=MF$ C. $left( MNP right)cap left( ACD right)=CD$ D. $left( MNP right)cap left( BCD right)=EF$ |
Lời giải chi tiết
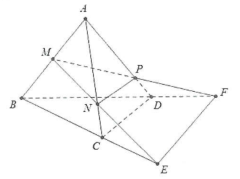
Điểm M, E cùng thuộc 2 mặt phẳng (MNP) và (ABC) do đó
$left( MNP right)cap left( ABC right)=ME.$
Tương tự: $left( MNP right)cap left( ABD right)=MF.$
+) $left( MNP right)cap left( ACD right)=NP$
+) $left( MNP right)cap left( BCD right)text{=EF}$
Khẳng định sai là C. Chọn C.
| Bài tập 10: Cho hình tứ diện ABCD, các điểm M và N lần lượt nằm trong tam giác ABD và ACD, AM cắt BD tại P, AN cắt CD tại Q, đường thẳng PQ cắt BC tại E. Khẳng định nào sau đây là sai?
A. $left( AMN right)cap left( BCD right)=PQ$ . B. $left( AMN right)cap left( ABC right)=AE$ . C. $left( AMN right)cap left( ABD right)=AE.$ D. $left( AMN right)cap left( ABD right)=AP$. |
Lời giải chi tiết
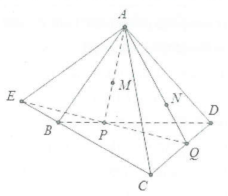
Hai mặt phẳng (AMN) và (BCD) có 2 điểm chung là P và Q do đó $left( AMN right)cap left( BCD right)=PQ.$
Vì $PQcap left( BC right)=ERightarrow E$ thuộc (APQ) và (ABC)
Hai mặt phẳng (AMN) và (ABC) có 2 điểm chung là A và E nên $left( AMN right)cap left( ABC right)=AE$ .
Hai mặt phẳng (AMN) và (ABD) có 2 điểm chung là A và P $left( AMN right)cap left( ABD right)=AP.$ Đáp án sai là C. Chọn C
