Các dạng toán trắc nghiệm tích vô hướng của hai vectơ trong không gian lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.
DẠNG 1: GÓC GIỮA HAI VECTƠ
Phương pháp
* Cho ba điểm $A,\,B,\,C$ ta có:
+ $\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}$$; $ $\left( {\overrightarrow {BA} ,\overrightarrow {CA} } \right) = \widehat {BAC}$ (Hai vectơ có cùng điểm đầu hoặc cùng điểm cuối)
+ $\left( {\overrightarrow {AB} ,\overrightarrow {CA} } \right) = {180^0} – \widehat {BAC}$$; $$\left( {\overrightarrow {BA} ,\overrightarrow {AC} } \right) = {180^0} – \widehat {BAC}$ (Hai vectơ có điểm đầu của vectơ này là điểm cuối của vectơ kia)
* $\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|cos\left( {\overrightarrow a ,\overrightarrow b } \right)$
* • $cos\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}$
• $\vec a \bot \vec b \Leftrightarrow \vec a.\vec b = 0$.
• Góc giữa hai vectơ cùng hướng và khác $\vec 0$ luôn bằng ${0^o}$.
• Góc giữa hai vectơ ngược hướng và khác luôn bằng ${180^o}$.

Câu 1. Cho hình lập phương $ABCD.A’B’C’D’$. Góc giữa hai vectơ $\overrightarrow {AB} $ và $\overrightarrow {DD’} $ bằng
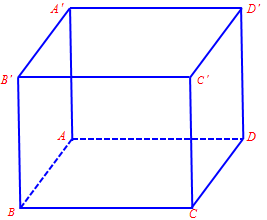
A. ${30^0}$. B. ${45^0}$. C. ${60^0}$. D. ${90^0}$.
Lời giải
Ta có: $\left( {\overrightarrow {AB} ,\,\overrightarrow {DD’} } \right) = \left( {\overrightarrow {AB} ,\,\overrightarrow {AA’} } \right) = {90^0}$ (vì $\overrightarrow {AB} \bot \,\overrightarrow {AA’} $)
Câu 2. Cho hình lập phương $ABCD.A’B’C’D’$. Góc giữa hai vectơ $\overrightarrow {BA’} $ và $\overrightarrow {DD’} $ bằng
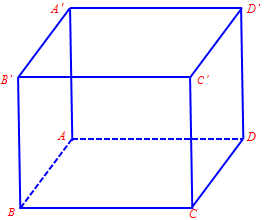
A. ${30^0}$. B. ${45^0}$. C. ${60^0}$. D. ${90^0}$.
Lời giải
Ta có: $\left( {\overrightarrow {BA’} ,\,\overrightarrow {DD’} } \right) = \left( {\overrightarrow {BA’} ,\,\overrightarrow {AA’} } \right) = \widehat {BA’A} = {45^0}$ (Hai vectơ có cùng cùng điểm cuối $A’$ )
Câu 3. Cho hình lập phương $ABCD.A’B’C’D’$. Góc giữa hai vectơ $\overrightarrow {BA} $ và $\overrightarrow {D’C} $ bằng
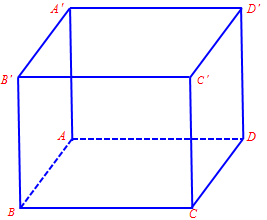
A. ${30^0}$. B. ${45^0}$. C. ${60^0}$. D. ${135^0}$.
Lời giải
Ta có: $\left( {\overrightarrow {BA} ,\,\overrightarrow {D’C} } \right) = \left( {\overrightarrow {BA} ,\,\overrightarrow {A’B} } \right) = {180^0} – \widehat {ABA’}$ $ = {180^0} – {45^0} = {135^0}$ (Hai vectơ có điểm đầu của vectơ này là điểm cuối của vectơ kia)
Câu 4. Cho hình lập phương $ABCD.A’B’C’D’$. Góc giữa hai vectơ $\overrightarrow {A’D} $ và $\overrightarrow {D’C} $ bằng
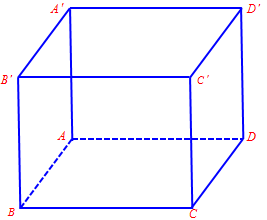
A. ${30^0}$. B. ${45^0}$. C. ${60^0}$. D. ${135^0}$.
Lời giải
Ta có: $\left( {\overrightarrow {A’D} ,\,\overrightarrow {D’C} } \right) = \left( {\overrightarrow {A’D} ,\,\overrightarrow {A’B} } \right) = \widehat {DA’B} = {60^0}$ (Tam giác $DA’B$ đều vì ba cạnh là ba đường chéo của ba hình vuông bằng nhau )
Câu 5. Cho hình lăng trụ tam giác đều $ABC.A’B’C’$. Góc giữa hai vectơ $\overrightarrow {A’C’} $ và $\overrightarrow {AB} $ bằng
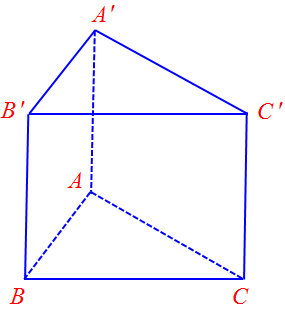
A. ${30^0}$. B. ${45^0}$. C. ${60^0}$. D. ${135^0}$.
Lời giải
Ta có: $\left( {\overrightarrow {A’C’} ,\,\overrightarrow {AB} } \right) = \left( {\overrightarrow {A’C’} ,\,\overrightarrow {A’B’} } \right) = \widehat {C’A’B’} = {60^0}$ (Tam giác $C’A’B’$ đều )
Câu 6. Cho hình lăng trụ tam giác đều $ABC.A’B’C’$. Góc giữa hai vectơ $\overrightarrow {BC} $ và $\overrightarrow {A’B’} $ bằng
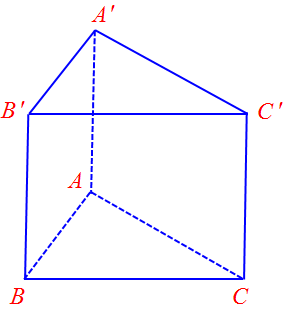
A. ${30^0}$. B. ${45^0}$. C. ${60^0}$. D. ${135^0}$.
Lời giải
Ta có: $\left( {\overrightarrow {BC} ,\,\overrightarrow {A’B’} } \right) = \left( {\overrightarrow {BC} ,\,\overrightarrow {AB} } \right) = {180^0} – \widehat {CBA}$ $ = {180^0} – {60^0} = {120^0}$(Tam giác $CBA$ đều )
Câu 7. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$. Tích vô hướng của hai vectơ $\overrightarrow {AB} $ và $\overrightarrow {A’C’} $ bằng
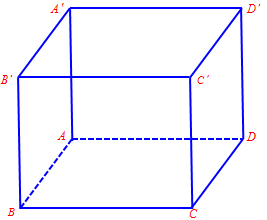
A. ${a^2}$. B. ${a^2}\sqrt 2 $. C. $ – {a^2}$. D. $\frac{{{a^2}\sqrt 2 }}{2}$.
Lời giải
Ta có: $\overrightarrow {AB} .\overrightarrow {A’C’} = \overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|cos\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)$
$ = AB.AC.cos\widehat {BAC} = a.a\sqrt 2 .cos{45^0} = {a^2}\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2}$
Câu 8. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$. Tích vô hướng của hai vectơ $\overrightarrow {BC’} $ và $\overrightarrow {B’A} $ bằng
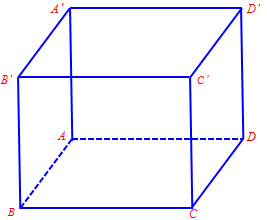
A. ${a^2}$. B. ${a^2}\sqrt 2 $. C. $ – {a^2}$. D. $\frac{{{a^2}\sqrt 2 }}{2}$.
Lời giải
Ta có: $\overrightarrow {BC’} .\overrightarrow {B’A} = \overrightarrow {BC’} .\overrightarrow {C’D} = \left| {\overrightarrow {BC’} } \right|.\left| {\overrightarrow {C’D} } \right|cos\left( {\overrightarrow {BC’} ,\overrightarrow {C’D} } \right)$
$ = BC’.C’D.cos\left( {{{180}^0} – \widehat {BC’D}} \right) = a\sqrt 2 .a\sqrt 2 .cos\left( {{{180}^0} – {{60}^0}} \right)$
$ = 2{a^2}.cos{120^0} = 2{a^2}.\left( { – \frac{1}{2}} \right) = – {a^2}$
Câu 9. Cho tứ diện đều $ABCD$ có cạnh bằng $a$ và $M$ là trung điểm của $CD$. Tích vô hướng của hai vectơ $\overrightarrow {BM} $ và $\overrightarrow {AC} $ bằng
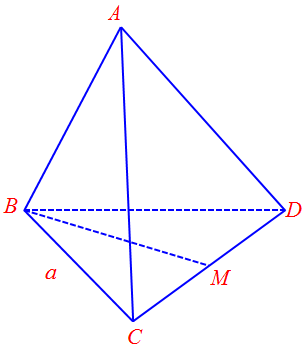
A. $\frac{{{a^2}}}{2}$. B. ${a^2}$. C. $ – {a^2}$. D. $\frac{{{a^2}}}{4}$.
Lời giải
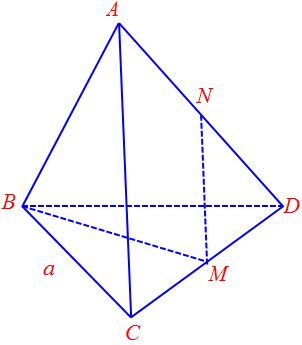
Gọi $N$ là trung điểm $AD$, ta có: $MN$ là đường trung bình tam giác $ACD$ nên $MN//AC$ và $MN = \frac{1}{2}AC$.
Ta có: $\overrightarrow {BM} .\overrightarrow {AC} = \overrightarrow {BM} .2\overrightarrow {NM} = 2\overrightarrow {BM} .\overrightarrow {NM} = $
$2\left| {\overrightarrow {BM} } \right|.\left| {\overrightarrow {NM} } \right|cos\left( {\overrightarrow {BM} ,\overrightarrow {NM} } \right) = 2BM.NMcos\widehat {BMN}$
$ = 2BM.NM.\frac{{B{M^2} + N{M^2} – B{N^2}}}{{2BM.NM}} = B{M^2} + N{M^2} – B{N^2}$
${\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} + {\left( {\frac{1}{2}a} \right)^2} – {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{{a^2}}}{4}$
Câu 10. Cho tứ diện $ABCD$ có $AB = AC = AD$ và $\widehat {BAC} = \widehat {BAD} = {60^0}$. Hãy xác định góc giữa cặp vectơ $\overrightarrow {AB} $ và $\overrightarrow {CD} $ ?
A. ${60^0}$. B. ${45^0}$. C. ${120^0}$. D. ${90^0}$.
Lời giải
Chọn D.
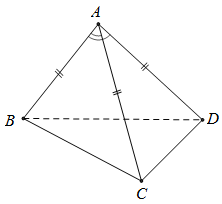
Ta có
$\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {AD} – \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} – \overrightarrow {AB} .\overrightarrow {AC} $
$ = AB.AD.\cos {60^0} – AB.AC.\cos {60^0} = 0$
$ \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = {90^0}$
Câu 11. Cho hình chóp $S.ABC$ có $SA = SB = SC$ và $\widehat {ASB} = \widehat {BSC} = \widehat {CSA}$. Hãy xác định góc giữa cặp vectơ $\overrightarrow {SA} $ và $\overrightarrow {BC} $?
A. ${120^0}$. B. ${90^0}$. C. ${60^0}$. D. ${45^0}$.
Lời giải
Chọn B.
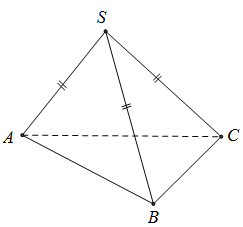
Ta có
$\overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .\left( {\overrightarrow {SC} – \overrightarrow {SB} } \right) = \overrightarrow {SA} .\overrightarrow {SC} – \overrightarrow {SA} .\overrightarrow {SB} $
$ = SA.SC.\cos \widehat {ASC} – SA.SB.\cos \widehat {ASB} = 0$
$ \Rightarrow \left( {\overrightarrow {SA} ,\overrightarrow {BC} } \right) = {90^0}$
Câu 12. Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh bằng $a$ và các cạnh bên đều bằng $a$. Gọi $M$ và $N$ lần lượt là trung điểm của $AD$ và $SD$. Số đo của góc $\left( {MN,SC} \right)$ bằng:
A. $45^\circ $ B. $30^\circ $ C. $90^\circ $ D. $60^\circ $
Lời giải
Chọn C.
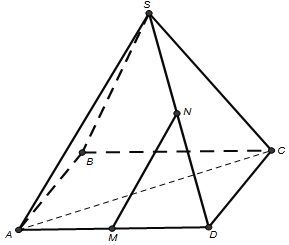
Ta có: $AC = a\sqrt 2 $
$ \Rightarrow A{C^2} = 2{a^2} = S{A^2} + S{C^2}$
$ \Rightarrow \Delta SAC$ vuông tại $S$.
Khi đó: $\overrightarrow {NM} .\overrightarrow {SC} = \frac{1}{2}\overrightarrow {SA} .\overrightarrow {SC} = 0 \Leftrightarrow \left( {\overrightarrow {NM} ,\overrightarrow {SC} } \right) = 90^\circ $$ \Rightarrow \left( {MN,SC} \right) = 90^\circ $
Câu 13. Cho tứ diện $ABCD$ đều cạnh bằng $a$. Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $BCD$. Góc giữa $AO$ và $CD$ bằng bao nhiêu ?
A. ${0^0}$. B. ${30^0}$. C. ${90^0}$. D. ${60^0}$.
Lời giải
Chọn C.
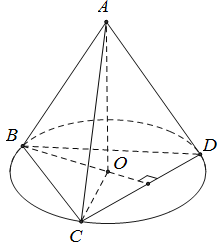
Ta có $\overrightarrow {AO} .\overrightarrow {CD} = \left( {\overrightarrow {CO} – \overrightarrow {CA} } \right)\overrightarrow {CD} $
$\begin{gathered}
= \overrightarrow {CO} .\overrightarrow {CD} – \overrightarrow {CA} .\overrightarrow {CD} = CO.CD.\cos {30^0} – CA.CD.\cos {60^0} \hfill \\
= \frac{{a\sqrt 3 }}{3}.a.\frac{{\sqrt 3 }}{2} – a.a.\frac{1}{2} = \frac{{{a^2}}}{2} – \frac{{{a^2}}}{2} = 0. \hfill \\
\end{gathered} $
Suy ra $AO \bot CD$.
Câu 14. Cho tứ diện $ABCD$ với $AB \bot AC,\,\,AB \bot BD$. Gọi $P,\,\,Q$ lần lượt là trung điểm của $AB$ và $CD$. Góc giữa $PQ$ và $AB$ là?
A. ${90^0}.$ B. ${60^0}.$ C. ${30^0}.$ D. ${45^0}.$
Lời giải
Chọn A.
$\overrightarrow {AB} .\overrightarrow {PQ} \Rightarrow AB \bot PQ$
Câu 15. Cho tứ diện$ABCD$ có $AB = AC = AD$ và $\widehat {BAC} = \widehat {BAD} = {60^0},\,\widehat {CAD} = {90^0}$. Gọi $I$ và $J$ lần lượt là trung điểm của $AB$ và $CD$. Hãy xác định góc giữa cặp vectơ $\overrightarrow {AB} $ và $\overrightarrow {IJ} $?
A. $120^\circ $. B. $90^\circ $. C. $60^\circ $. D. $45^\circ $.
Lời giải
Chọn B.
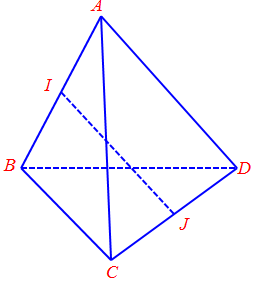
Xét tam giác$ICD$ có $J$ là trung điểm đoạn $CD$.
Ta có: $\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right)$
Vì tam giác $ABC$ có $AB = AC$ và $\widehat {BAC} = 60^\circ $
Nên tam giác $ABC$đều. Suy ra: $CI \bot AB$
Tương tự ta có tam giác $ABD$ đều nên $DI \bot AB$.
Xét $\overrightarrow {IJ} .\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {IC} + \overrightarrow {ID} } \right).\overrightarrow {AB} = \frac{1}{2}\overrightarrow {IC} .\overrightarrow {AB} + \frac{1}{2}\overrightarrow {ID} .\overrightarrow {AB} = \overrightarrow 0 $.
Suy ra $\overrightarrow {IJ} \bot \overrightarrow {AB} $. Hay góc giữa cặp vectơ $\overrightarrow {AB} $ và $\overrightarrow {IJ} $ bằng ${90^0}$.
Câu 16. Cho tứ diện $ABCD$ có hai mặt $ABC$ và $ABD$ là các tam giác đều. Khẳng định nào sau đây đúng nhất.
A. AB và CD chéo nhau B. AB và CD vuông góc với nhau
C. AB và CD đồng phẳng D. AB và CD cắt nhau
Lời giải
Chọn B.
Đặt $AB = AD = AC = a$
Ta có $\overrightarrow {CD} .\overrightarrow {AB} = \left( {\overrightarrow {AD} – \overrightarrow {AC} } \right)\overrightarrow {AB} $
$ = \left| {\overrightarrow {AB} } \right|\left| {\overrightarrow {AD} } \right|\cos {60^0} – \left| {\overrightarrow {AB} } \right|\left| {\overrightarrow {AC} } \right|\cos {60^0}$$ = a.a.\frac{1}{2} – a.a.\frac{1}{2} = 0$
Vậy $AB \bot CD$.
Câu 17. Cho hình lăng trụ tam giác đều $ABC.A’B’C’$ có $AB = a$ và $AA’ = \sqrt 2 \,a$. Góc giữa hai đường thẳng $AB’$ và $BC’$ bằng
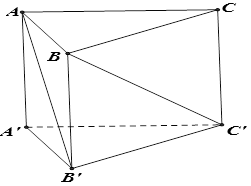
A. $60^\circ $. B. $45^\circ $. C. $90^\circ $. D. $30^\circ $.
Lời giải
Chọn A
Ta có $\overrightarrow {AB’} .\overrightarrow {BC’} = \left( {\overrightarrow {AB} + \overrightarrow {BB’} } \right)\left( {\overrightarrow {BC} + \overrightarrow {CC’} } \right)$$ = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC’} + \overrightarrow {BB’} .\overrightarrow {BC} + \overrightarrow {BB’} .\overrightarrow {CC’} $
$ = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC’} + \overrightarrow {BB’} .\overrightarrow {BC} + \overrightarrow {BB’} .\overrightarrow {CC’} $$ = – \frac{{{a^2}}}{2} + 0 + 0 + 2{a^2} = \frac{{3{a^2}}}{2}$.
Suy ra $\cos \left( {\overrightarrow {AB’} ,\overrightarrow {BC’} } \right) = \frac{{\overrightarrow {AB’} .\overrightarrow {BC’} }}{{\left| {\overrightarrow {AB’} } \right|.\left| {\overrightarrow {BC’} } \right|}}$$ = \frac{{\frac{{3{a^2}}}{2}}}{{a\sqrt 3 .a\sqrt 3 }} = \frac{1}{2}$
$ \Rightarrow \widehat {\left( {AB’,BC’} \right)} = 60^\circ $.
Câu 18. Cho hình lập phương $ABCD.{A_1}{B_1}{C_1}{D_1}$ có cạnh $a$. Gọi $M$ là trung điểm $AD$. Giá trị $\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} $ là:
A. $\frac{1}{2}{a^2}$. B. ${a^2}$. C. $\frac{3}{4}{a^2}$. D. $\frac{3}{2}{a^2}$.
Lời giải
Chọn A.
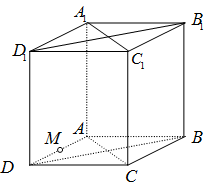
Ta có: $\overrightarrow {{B_1}M} .\overrightarrow {B{D_1}} = \left( {\overrightarrow {{B_1}B} + \overrightarrow {BA} + \overrightarrow {AM} } \right)\left( {\overrightarrow {BA} + \overrightarrow {AD} + \overrightarrow {D{D_1}} } \right)$
$ = \overrightarrow {{B_1}B} .\overrightarrow {D{D_1}} + {\overrightarrow {BA} ^2} + \overrightarrow {AM} .\overrightarrow {AD} $
$ = – {a^2} + {a^2} + \frac{{{a^2}}}{2} = \frac{{{a^2}}}{2}$
Câu 19. Cho hình lập phương $ABCD.EFGH$. Hãy xác định góc giữa cặp vectơ $\overrightarrow {AB} $ và$\overrightarrow {EG} $?
A. $90^\circ $ B. $60^\circ $ C. $45^\circ $ D. $120^\circ $
Lời giải
Chọn C.
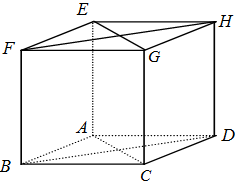
Ta có: $EG//AC$ (do $ACGE$ là hình chữ nhật)
$ \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {EG} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = 45^\circ $
Câu 20. Cho hình lập phương $ABCD.A’B’C’D’$. Gọi $M$, $N$ lần lượt là trung điểm của $AD$, $BB’.$ Cosin của góc hợp bởi $MN$ và $AC’$ bằng
A. $\frac{{\sqrt 3 }}{3}$. B. $\frac{{\sqrt 2 }}{3}$. C. $\frac{{\sqrt 5 }}{3}$. D. $\frac{{\sqrt 2 }}{4}$.
Lời giải
Chọn B
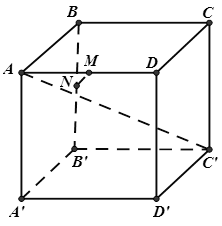
* Xét hình lập phương $ABCD.A’B’C’D’$ cạnh $a$.
* Đặt $\overrightarrow a = \overrightarrow {AB} , \overrightarrow b = \overrightarrow {AD} , \overrightarrow c = \overrightarrow {AA’} $
$ \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = \left| {\overrightarrow c } \right| = a, \overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow c = \overrightarrow a .\overrightarrow c = 0$.
* Ta có:
$\overrightarrow {MN} = \overrightarrow {AN} – \overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BN} – \overrightarrow {AM} $
$ = \overrightarrow a – \frac{1}{2}\overrightarrow b + \frac{1}{2}\overrightarrow c $$ \Rightarrow \left| {\overrightarrow {MN} } \right| = \sqrt {{a^2} + \frac{1}{4}{a^2} + \frac{1}{4}{a^2}} = \frac{{a\sqrt 3 }}{{\sqrt 2 }}$
$\overrightarrow {AC’} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow a + \overrightarrow b + \overrightarrow c $
$ \Rightarrow \left| {\overrightarrow {AC’} } \right| = \;\sqrt {{a^2} + {a^2} + {a^2}} = a\sqrt 3 $
$\overrightarrow {AC’} .\overrightarrow {MN} = {a^2} – \frac{1}{2}{a^2} + \frac{1}{2}{a^2} = {a^2}$
$\cos \left( {MN;AC’} \right) = \left| {\cos \left( {\overrightarrow {MN} ;\overrightarrow {AC’} } \right)} \right| = \frac{{\left| {\overrightarrow {MN} .\overrightarrow {AC’} } \right|}}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {AC’} } \right|}} = \frac{{\sqrt 2 }}{3}$.
Câu 21. Cho hình lăng trụ $ABC.A’B’C’$ có đáy $ABC$ là tam giác đều cạnh $a$, tam giác $A’BC$ đều nằm trong mặt phẳng vuông góc với $\left( {ABC} \right)$. $M$ là trung điểm cạnh $CC’$. Tính cosin góc $\alpha $ giữa hai đường thẳng $AA’$ và $BM$.
A. $\cos \alpha = \frac{{2\sqrt {22} }}{{11}}$. B. $\cos \alpha = \frac{{\sqrt {33} }}{{11}}$. C. $\cos \alpha = \frac{{\sqrt {11} }}{{11}}$. D. $\cos \alpha = \frac{{\sqrt {22} }}{{11}}$.
Lời giải
Chọn B
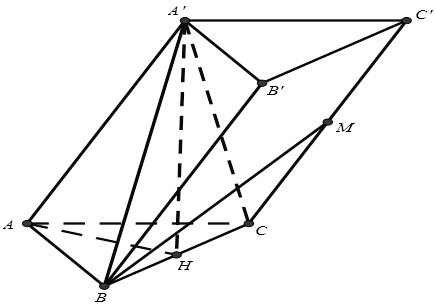
Ta có: $AH = A’H = \frac{{a\sqrt 3 }}{2}$ và $AH \bot BC,A’H \bot BC$$ \Rightarrow BC \bot \left( {AA’H} \right)$$ \Rightarrow BC \bot AA’$ hay
$BC \bot BB’$. Do đó: $BCC’B’$ là hình chữ nhật.
Khi đó: $CC’ = AA’ = \frac{{a\sqrt 3 }}{2}.\sqrt 2 = \frac{{a\sqrt 6 }}{2}$$ \Rightarrow BM = \sqrt {{a^2} + \frac{{{a^2}.6}}{{16}}} = a\frac{{\sqrt {22} }}{4}$.
Xét: $\overrightarrow {AA’} .\overrightarrow {BM} = \overrightarrow {AA’} .\left( {\overrightarrow {BC} + \overrightarrow {CM} } \right)$$ = 0 + AA’.CM$$ = \frac{{3{a^2}}}{4}$.
Suy ra $\cos \left( {AA’,BM} \right) = \frac{{\left| {\frac{{3{a^2}}}{4}} \right|}}{{\frac{{a\sqrt 6 }}{2}.\frac{{a\sqrt {22} }}{4}}}$$ = \frac{{\sqrt {33} }}{{11}}$.
Câu 22. Cho tam giác $ABC$, thì công thức tính diện tích nào sau đây là đúng nhất.
A. $S = \frac{1}{2}\sqrt {A{B^2}A{C^2} – B{C^2}} $ B. $S = \frac{1}{2}\sqrt {A{B^2}A{C^2} + \frac{1}{2}{{\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)}^2}} $
C. $S = \frac{1}{2}\sqrt {A{B^2}A{C^2} – \frac{1}{2}{{\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)}^2}} $ D. $S = \frac{1}{2}\sqrt {A{B^2}A{C^2} – {{\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)}^2}} $
Lời giải
Chọn D.
${S_{ABC}} = \frac{1}{2}ABAC\sin A = \frac{1}{2}\sqrt {A{B^2}A{B^2}{{\sin }^2}A} $
$ = \frac{1}{2}\sqrt {A{B^2}A{C^2}\left( {1 – {{\cos }^2}A} \right)} $$ = \frac{1}{2}\sqrt {A{B^2}A{C^2} – {{\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)}^2}} $.
Câu 23. Trong không gian cho ba điểm $A{,^{}}B{,^{}}C$ bất kỳ, chọn đẳng thức đúng?
A. $2\overrightarrow {AB} .\overrightarrow {AC} = A{B^2} + A{C^2} – B{C^2}$ B. $2\overrightarrow {AB} .\overrightarrow {AC} = A{B^2} + A{C^2} – 2B{C^2}$
C. $\overrightarrow {AB} .\overrightarrow {AC} = A{B^2} + A{C^2} – 2B{C^2}$ D. $\overrightarrow {AB} .\overrightarrow {AC} = A{B^2} + A{C^2} – B{C^2}$
Lời giải
Chọn A.
$B{C^2} = A{B^2} + A{C^2} – 2AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = A{B^2} + A{C^2} – 2.\overrightarrow {AB} .\overrightarrow {AC} $
Câu 24. Cho hình lập phương $ABCD.EFGH$ có cạnh bằng $a$. Ta có $\overrightarrow {AB} .\overrightarrow {EG} $ bằng?
A. ${a^2}\sqrt 2 $. B. ${a^2}$. C. ${a^2}\sqrt 3 $. D. $\frac{{{a^2}\sqrt 2 }}{2}$.
Lời giải
Chọn B.
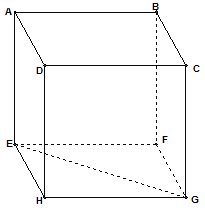
$\overrightarrow {AB} .\overrightarrow {EG} = \overrightarrow {AB} .\left( {\overrightarrow {EF} + \overrightarrow {EH} } \right) = \overrightarrow {AB} .\overrightarrow {EF} + \overrightarrow {AB} \overrightarrow {.EH} $$ = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} \,\,(\overrightarrow {EH} = \overrightarrow {AD} )$$ = {a^2}$ (Vì $\overrightarrow {AB} \bot \overrightarrow {AD} $)
Câu 25. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$. Hãy tìm mệnh đề sai trong những mệnh đề sau đây:
A. $2\overrightarrow {AB} + \overrightarrow {B’C’} + \overrightarrow {CD} + \overrightarrow {D’A’} = \overrightarrow 0 $ B. $\overrightarrow {AD’} .\overrightarrow {AB’} = {a^2}$
C. $\overrightarrow {AB’} .\overrightarrow {CD’} = 0$ D. $\left| {\overrightarrow {AC’} } \right| = a\sqrt 3 $.
Lời giải
Chọn A.
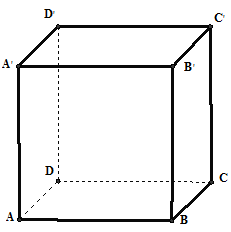
Ta có :$\,2\overrightarrow {AB} + \overrightarrow {B’C’} + \overrightarrow {CD} + \overrightarrow {D’A’} = \overrightarrow 0 $
$ \Leftrightarrow \overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {CD} } \right) + \left( {\overrightarrow {B’C’} + \overrightarrow {D’A’} } \right) = \overrightarrow 0 $
$ \Leftrightarrow \overrightarrow {AB} + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \Leftrightarrow \overrightarrow {AB} = \overrightarrow 0 $(vô lí)$\begin{gathered}
\,\,\,\,\,\,\,\,\, \hfill \\
\hfill \\
\hfill \\
\end{gathered} $
Câu 26. Cho tứ diện $ABCD$ với $AC = \frac{3}{2}AD,\widehat {CAB} = \widehat {DAB} = {60^0},CD = AD$. Gọi $\varphi $ là góc giữa $AB$ và $CD$. Chọn khẳng định đúng ?
A. $\cos \;\varphi = \frac{3}{4}$. B. $\varphi = {60^0}$. C. $\varphi = {30^0}$. D. $\cos \;\varphi = \frac{1}{4}$.
Lời giải
Chọn D.
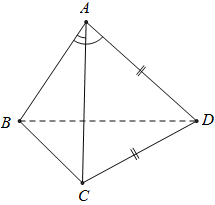
Ta có $\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = \frac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{AB.CD}}$
Mặt khác
$ = \overrightarrow {AB} \left( {\overrightarrow {AD} – \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} – \overrightarrow {AB} .\overrightarrow {AC} $
$ = AB.AD.\cos {60^0} – AB.AC.\cos {60^0}$
$ = AB.AD.\frac{1}{2} – AB.\frac{3}{2}AD.\frac{1}{2} = – \frac{1}{4}AB.AD = – \frac{1}{4}AB.CD$
Do có $\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \frac{{ – \frac{1}{4}AB.CD}}{{AB.CD}} = – \frac{1}{4}$. Suy ra $\cos \varphi = \frac{1}{4}$.
Câu 27. Cho tứ diện đều $ABCD$, $M$ là trung điểm của cạnh $BC$. Khi đó $\cos \left( {AB,DM} \right)$ bằng
A. $\frac{{\sqrt 2 }}{2}$. B. $\frac{{\sqrt 3 }}{6}$. C. $\frac{1}{2}$. D. $\frac{{\sqrt 3 }}{2}$.
Lời giải
Chọn B.
Giả sử cạnh của tứ diện là $a$.
Ta có $\cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {DM} } \right|}} = \frac{{\overrightarrow {AB} .\overrightarrow {DM} }}{{a.\frac{{a\sqrt 3 }}{2}}}$
Mặt khác
$\overrightarrow {AB} .\overrightarrow {DM} = \overrightarrow {AB} \left( {\overrightarrow {AM} – \overrightarrow {AD} } \right) = \overrightarrow {AB} .\overrightarrow {AM} – \overrightarrow {AB} .\overrightarrow {AD} $
$\begin{gathered}
= AB.AM.\cos {30^0} – AB.AD.\cos {60^0} \hfill \\
\hfill \\
\end{gathered} $
$ = a.\frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} – a.a.\frac{1}{2} = \frac{{3{a^2}}}{4} – \frac{{{a^2}}}{2} = \frac{{{a^2}}}{4}.$
Do có $\cos \left( {\overrightarrow {AB} ,\overrightarrow {DM} } \right) = \frac{{\sqrt 3 }}{6}$. Suy ra $\cos \left( {AB,DM} \right) = \frac{{\sqrt 3 }}{6}$.
DẠNG 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
Câu 28. Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn điều kiện $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 2$ và $\left( {\overrightarrow a ,\overrightarrow b } \right) = {30^0}.$ Tính tích vô hướng của $\overrightarrow a $ và $\overrightarrow b $.
A. $\overrightarrow a .\overrightarrow b = 2\sqrt 3 $. B. $\overrightarrow a .\overrightarrow b = 0$. C. $\overrightarrow a .\overrightarrow b = 2$. D. $\overrightarrow a .\overrightarrow b = \sqrt 3 $.
Lời giải
Chọn A.
$\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|cos\left( {\overrightarrow a ,\overrightarrow b } \right) = 2.2cos{30^0}$ $ = 4.\frac{{\sqrt 3 }}{2} = 2\sqrt 3 $
Câu 29. Cho $\overrightarrow a $ và $\overrightarrow b $ là hai vectơ cùng hướng và đều khác vectơ $\overrightarrow 0 $. Tính tích vô hướng của $\overrightarrow a $ và $\overrightarrow b $.
A. $\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$. B. $\overrightarrow a .\overrightarrow b = 0$. C. $\overrightarrow a .\overrightarrow b = – 1$. D. $\overrightarrow a .\overrightarrow b = – \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$.
Lời giải
Chọn A
Do $\overrightarrow a $ và $\overrightarrow b $ là hai vectơ cùng hướng nên $\left( {\overrightarrow a ,\overrightarrow b } \right) = {0^0} \Rightarrow cos\left( {\overrightarrow a ,\overrightarrow b } \right) = 1$.
Vậy $\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$.
Câu 30. Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ khác $\overrightarrow 0 $. Xác định góc $\alpha $ giữa hai vectơ $\overrightarrow a $ và $\overrightarrow b $ khi $\overrightarrow a .\overrightarrow b = – \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.$
A. $\alpha = {180^o}$. B. $\alpha = {0^o}$. C. $\alpha = {90^o}$. D. $\alpha = {45^o}$.
Lời giải
Chọn A
Mà theo giả thiết $\overrightarrow a .\overrightarrow b = – \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$, suy ra $\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = – 1 \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {180^0}$
Câu 31. Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn $\left| {\overrightarrow a } \right| = 3,$ $\left| {\overrightarrow b } \right| = 2$ và $\vec a.\vec b = – 3.$ Xác định góc $\alpha $ giữa hai vectơ $\overrightarrow a $ và $\overrightarrow b $
A. $\alpha = {30^o}$. B. $\alpha = {45^o}$. C. $\alpha = {60^o}$. D. $\alpha = {120^o}$.
Lời giải
Chọn D
Ta có $\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.cos\left( {\overrightarrow a ,\overrightarrow b } \right)$
$ \Rightarrow cos\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\vec a.\overrightarrow b }}{{\left| {\vec a} \right|.\left| {\overrightarrow b } \right|}} = \frac{{ – 3}}{{3.2}} = – \frac{1}{2}$
$ \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^0}$
Câu 32. Cho hai vectơ $\vec a$ và $\overrightarrow b $ thỏa mãn $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1$ và hai vectơ $\vec u = \frac{2}{5}\overrightarrow a – 3\overrightarrow b $ và $\vec v = \overrightarrow a + \overrightarrow b $ vuông góc với nhau. Xác định góc $\alpha $ giữa hai vectơ $\overrightarrow a $ và $\overrightarrow b .$
A. $\alpha = {90^o}$. B. $\alpha = {180^o}$. C. $\alpha = {60^o}$. D. $\alpha = {45^o}$.
Lời giải
Chọn B
Ta có $\vec u \bot \vec v \Leftrightarrow \vec u.\vec v = 0$
$ \Leftrightarrow \left( {\frac{2}{5}\overrightarrow a – 3\overrightarrow b } \right)\left( {\overrightarrow a + \overrightarrow b } \right) = 0 \Leftrightarrow \frac{2}{5}{\overrightarrow a ^2} – \frac{{13}}{5}\overrightarrow a \overrightarrow b – 3{\overrightarrow b ^2} = 0$
$ \Leftrightarrow \frac{2}{5}{.1^2} – \frac{{13}}{5}\overrightarrow a \overrightarrow b – {3.1^2} = 0 \Leftrightarrow – \frac{{13}}{5}\overrightarrow a \overrightarrow b – \frac{{13}}{5} = 0$ (Do $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1$)
$ \Rightarrow \overrightarrow a \overrightarrow b = – 1$
Suy ra $cos\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\vec a.\overrightarrow b }}{{\left| {\vec a} \right|.\left| {\overrightarrow b } \right|}} = \frac{{ – 1}}{{1.1}} = – 1$$ \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {180^0}$
Câu 33. Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn điều kiện $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1$ và $\overrightarrow a .\overrightarrow b = 3.$ Độ dài vectơ $3\overrightarrow a + 5\overrightarrow b :$
A. $5\sqrt 5 .$ B. $\sqrt {24} .$ C. 8. D. 124.
Lời giải
Chọn B.
${\left( {3\overrightarrow a + 5\overrightarrow b } \right)^2} = 9{\overrightarrow a ^2} + 30\overrightarrow a \overrightarrow b + 25{\overrightarrow b ^2}$ $ = 9 + 90 + 25 = 124.$
$ \Rightarrow \left| {3\overrightarrow a + 5\overrightarrow b } \right| = \sqrt {124} $
Câu 34. Cho $\vec a,\vec b$ có $(\vec a + 2\vec b)$ vuông góc với vectơ $(5\vec a – 4\vec b)$ và $|\vec a| = |\vec b|$. Khi đó:
A. $\cos (\vec a,\vec b) = \frac{{\sqrt 2 }}{2}$. B. $\cos (\vec a,\vec b) = {90^\circ }$. C. $\cos (\vec a,\vec b) = \frac{{\sqrt 3 }}{2}$. D. $\cos (\vec a,\vec b) = \frac{1}{2}$
Lời giải
Chọn D.
+Do $(\vec a + 2\vec b)$ vuông góc với vectơ $(5\vec a – 4\vec b)$ nên:
$(\vec a + 2\vec b) \cdot (5\vec a – 4\vec b) = 0 \Leftrightarrow 5{\vec a^2} – 8{\vec b^2} + 6\vec a \cdot \vec b = 0$
$ \Leftrightarrow \vec a \cdot \vec b = \frac{{ – 5{{\vec a}^2} + 8{{\vec b}^2}}}{6}. $
Ta có $|\vec a| = |\vec b| \Leftrightarrow |\vec a{|^2} = |\vec b{|^2}$. Suy ra $\vec a \cdot \vec b = \frac{{3{{\vec a}^2}}}{6}$
$ + \cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a||\vec b|}} = \frac{{\frac{{3{{\vec a}^2}}}{6}}}{{{{\vec a}^2}}} = \frac{1}{2}$
Câu 35. Cho hai vectơ $\overrightarrow a ,\overrightarrow b $ thỏa mãn: $\left| {\overrightarrow a } \right| = 4;\left| {\overrightarrow b } \right| = 3;\left| {\overrightarrow a – \overrightarrow b } \right| = 4$. Gọi $\alpha $ là góc giữa hai vectơ $\overrightarrow a ,\overrightarrow b $. Chọn khẳng định đúng?
A. $\cos \alpha = \frac{3}{8}$. B. $\alpha = {30^0}$. C. $\cos \alpha = \frac{1}{3}$. D. $\alpha = {60^0}$.
Lời giải
Chọn A.
${(\overrightarrow a – \overrightarrow b )^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} – 2\overrightarrow a .\overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = \frac{9}{2}.$
Do đó: $\cos \;\alpha = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{3}{8}$.
Câu 36. $\vec u$ và $\vec v$ là 2 vectơ đều khác $\vec 0$. Khi đó $|\vec u + 2\vec v{|^2}$ bằng
A. ${\vec u^2} + 2{\vec v^2} – 4\vec u \cdot \vec v$. B. ${\vec u^2} + 4{\vec v^2} + 4\vec u \cdot \vec v$. C. ${\vec u^2} + 4{\vec v^2}$. D. $4\vec u \cdot \vec v(\vec u – \vec v)$.
Lời giải
Chọn B.
Ta có $|\vec u + 2\vec v{|^2} = {(\vec u + 2\vec v)^2} = {\vec u^2} + 4{\vec v^2} + 4\vec u \cdot \vec v$.
Câu 37. Cho hai vectơ $\vec a$ và $\vec b$ có $|\vec a| = 5,|\vec b| = 12$ và $|\vec a + \vec b| = 13$. Khi đó cosin của góc giữa hai vectơ $\vec a – \vec b$ và $\vec a + \vec b$ bằng
A. $\frac{{12}}{{13}}$. B. $\frac{5}{{12}}$. C. $ – \frac{{119}}{{169}}$. D. $\frac{{119}}{{169}}$.
Lời giải
Chọn C.
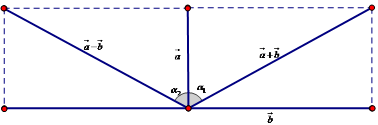
Ta thấy $\sqrt {{5^2} + {{12}^2}} = 13$ suy ra $\vec a \bot \vec b$
Mặt khác: $\cos \left( {{\alpha _2}} \right) = \frac{{|\vec a|}}{{|\vec a + \vec b|}} = \frac{5}{{13}} \Rightarrow {\alpha _2} = {\cos ^{ – 1}}\frac{5}{{13}}$.
Do đó góc giữa hai vectơ $\vec a – \vec b$ và $\vec a + \vec b$ bằng ${\alpha _1} + {\alpha _2} = 2{\alpha _2} = 2{\cos ^{ – 1}}\frac{5}{{13}}$
Vậy $\cos (\overrightarrow {\vec a – \vec b,\vec a + \vec b} ) = \cos \left( {2 \cdot {{\cos }^{ – 1}}\frac{5}{{13}}} \right) = – \frac{{119}}{{169}}$.
Câu 38. Cho $\vec u = \vec a + 3\vec b$ vuông góc với $\vec v = 7\vec a – 5\vec b$ và $\vec x = \vec a – 4\vec b$ vuông góc với $\vec y = 7\vec a – 2\vec b$. Khi đó góc giữa hai vectơ $\vec a$ và $\vec b$ bằng
A. $(\vec a,\vec b) = {75^\circ }$. B. $(\vec a,\vec b) = {60^\circ }$. C. $(\vec a,\vec b) = {120^\circ }$. D. $(\vec a,\vec b) = {45^\circ }$.
Lời giải
Chọn B.
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{\vec u \cdot \vec v = 0} \\
{\vec x \cdot \vec y = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{(\vec a + 3\vec b) \cdot (7\vec a – 5\vec b) = 0} \\
{(\vec a – 4\vec b) \cdot (7\vec a – 2\vec b) = 0}
\end{array}} \right.} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{7|\vec a{|^2} – 15|\vec b{|^2} = – 16\vec a \cdot \vec b} \\
{7|\vec a{|^2} + 8|\vec b{|^2} = 30\vec a \cdot \vec b}
\end{array}} \right.. $
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{|\vec b{|^2} = 2\vec a\vec b} \\
{|\vec a{|^2} = 2\vec a \cdot \vec b}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{|\vec b{|^2} = 2\vec a \cdot \vec b} \\
{|\vec a| = |\vec b|}
\end{array}} \right.} \right.$
Từ đó, ta có: $\cos (\vec a,\vec b) = \frac{{\vec a\vec b}}{{|\vec a| \cdot |\vec b|}} = \frac{{\vec a \cdot \vec b}}{{|\vec b{|^2}}} = \frac{1}{2} \Rightarrow (\vec a,\vec b) = {60^\circ }$
Câu 39. Cho hai vectơ $\overrightarrow a ,\overrightarrow b $ thỏa mãn: $\left| {\overrightarrow a } \right| = 4;\left| {\overrightarrow b } \right| = 3;\overrightarrow a .\overrightarrow b = 10$. Xét hai vectơ $\overrightarrow y = \overrightarrow a – \overrightarrow b $$\overrightarrow x = \overrightarrow a – 2\overrightarrow b ,$. Gọi α là góc giữa hai vectơ $\overrightarrow x ,\overrightarrow y $. Chọn khẳng định đúng.
A. $\cos \alpha = \frac{{ – 2}}{{\sqrt {15} }}$. B. $\cos \alpha = \frac{1}{{\sqrt {15} }}$. C. $\cos \alpha = \frac{3}{{\sqrt {15} }}$. D. $\cos \alpha = \frac{2}{{\sqrt {15} }}$.
Lời giải
Chọn D.
Ta có $\overrightarrow x .\overrightarrow y = \left( {\overrightarrow a – 2\overrightarrow b } \right)\left( {\overrightarrow a – \overrightarrow b } \right) = {\left( {\overrightarrow a } \right)^2} + 2{\left( {\overrightarrow b } \right)^2} – 3\overrightarrow a .\overrightarrow b = 4$.
$\left| {\overrightarrow x } \right| = \sqrt {{{\left( {\overrightarrow x } \right)}^2}} = \sqrt {{{\left( {\overrightarrow a – 2\overrightarrow b } \right)}^2}} = \sqrt {{{\left( {\overrightarrow a } \right)}^2} + 4{{\left( {\overrightarrow b } \right)}^2} – 4\overrightarrow a .\overrightarrow b } = 2\sqrt 3 $.
$\left| {\overrightarrow y } \right| = \sqrt {{{\left( {\overrightarrow y } \right)}^2}} = \sqrt {{{\left( {\overrightarrow a – \overrightarrow b } \right)}^2}} = \sqrt {{{\left( {\overrightarrow a } \right)}^2} + {{\left( {\overrightarrow b } \right)}^2} – 2\overrightarrow a .\overrightarrow b } = \sqrt 5 $.
$\cos \alpha = \frac{{\overrightarrow x .\overrightarrow y }}{{\left| {\overrightarrow x } \right|.\left| {\overrightarrow y } \right|}} = \frac{4}{{2\sqrt 3 .\sqrt 5 }} = \frac{2}{{\sqrt {15} }}$
Câu 40. Cho hai vectơ $\overrightarrow a ,\overrightarrow b $ thỏa mãn: $\left| {\overrightarrow a } \right| = 26;\left| {\overrightarrow b } \right| = 28;\left| {\overrightarrow a + \overrightarrow b } \right| = 48$. Độ dài vectơ $\overrightarrow a – \overrightarrow b $ bằng?
A. $25.$ B. $\sqrt {616} $. C. $9.$ D. $\sqrt {618} $.
Lời giải
Chọn B.
${\left| {\overrightarrow a – \overrightarrow b } \right|^2} = {\left( {\overrightarrow a – \overrightarrow b } \right)^2} = {\overrightarrow a ^2} + {\overrightarrow b ^2} – 2\overrightarrow a .\overrightarrow b $
$ = 2\left( {{{\overrightarrow a }^2} + {{\overrightarrow b }^2}} \right) – {\left( {\overrightarrow a + \overrightarrow b } \right)^2}$
$ = 2\left( {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2}} \right) – {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = 2\left( {{{26}^2} + {{28}^2}} \right) – {48^2} = 616$
$ \Rightarrow \left| {\overrightarrow a – \overrightarrow b } \right| = \sqrt {616} .$
———-
