Các dạng toán trả lời ngắn tích vô hướng của hai vectơ trong không gian lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.
DẠNG 1: GÓC GIỮA HAI VECTƠ
Câu 1. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và mặt bên $SAB$ là tam giác đều. Tính góc giữa hai vectơ $\overrightarrow {DC} $ và $\overrightarrow {BS} $.
Lời giải
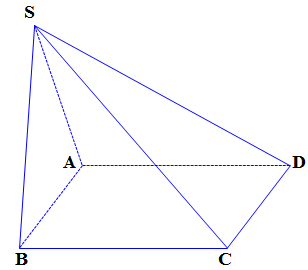
Ta có: $\left( {\overrightarrow {DC} ,\,\overrightarrow {BS} } \right) = \left( {\overrightarrow {AB} ,\,\overrightarrow {BS} } \right) = {180^0} – \widehat {ABS} = {180^0} – 60 = {120^0}$.
Câu 2. Cho tứ diện $ABCD$ có $DA = DB = a,BC = \frac{a}{2}$, $AB \bot BC$ và $CBD = {45^\circ }$. Tính góc giữa hai vectơ $\overrightarrow {AD} $ và $\overrightarrow {BC} $.
Lời giải
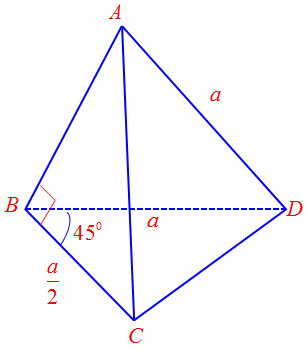
Ta có:
+ $\cos (\overrightarrow {AD} ,\overrightarrow {BC} ) = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \cdot |\overrightarrow {BC} |}} = \frac{{\left( {\overrightarrow {BD} – \overrightarrow {BA} } \right) \cdot \overrightarrow {BC} }}{{a.\frac{a}{2}}}$
$ = \frac{{\overrightarrow {BD} .\overrightarrow {BC} – \overrightarrow {BA} \cdot \overrightarrow {BC} }}{{\frac{{{a^2}}}{2}}}$
+ $\overrightarrow {BD} .\overrightarrow {BC} = \left| {\overrightarrow {BD} } \right|.\left| {\overrightarrow {BC} } \right|.cos\left( {\overrightarrow {BD} ,\overrightarrow {BC} } \right) = a.\frac{a}{2}.cos\widehat {DBC}$
$ = \frac{{{a^2}}}{2}.cos{45^0} = \frac{{{a^2}}}{2}.\frac{{\sqrt 2 }}{2} = \frac{{{a^2}\sqrt 2 }}{4}$.
+ $\overrightarrow {BA} \cdot \overrightarrow {BC} = 0$ (Do $AB \bot BC$).
Suy ra $\cos (\overrightarrow {AD} ,\overrightarrow {BC} ) = \frac{{\frac{{{a^2}\sqrt 2 }}{4} – 0}}{{\frac{{{a^2}}}{2}}} = \frac{{\sqrt 2 }}{2}$
Vậy $(\overrightarrow {AD} ,\overrightarrow {BC} ) = {45^0}$
Câu 3. Cho hình chóp $S.ABC$ có $SA = SB = SC = AB = AC = a$ và $BC = a\sqrt 2 $. Tính góc giữa các vectơ $\overrightarrow {SC} $ và $\overrightarrow {AB} $.
Lời giải
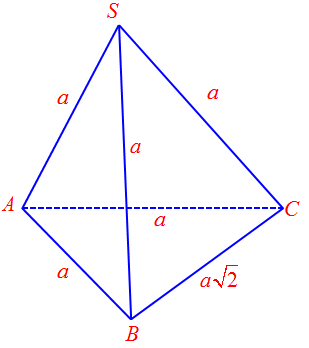
Ta có:
+ $\cos (\overrightarrow {SC} ,\overrightarrow {AB} ) = \frac{{\overrightarrow {SC} \cdot \overrightarrow {AB} }}{{|\overrightarrow {SC} | \cdot |\overrightarrow {AB} |}}$
$ = \frac{{(\overrightarrow {SA} + \overrightarrow {AC} ) \cdot \overrightarrow {AB} }}{{a.a}} = \frac{{\overrightarrow {SA} \cdot \overrightarrow {AB} + \overrightarrow {AC} \cdot \overrightarrow {AB} }}{{{a^2}}}$
+ $\overrightarrow {SA} \cdot \overrightarrow {AB} = \left| {\overrightarrow {SA} } \right| \cdot \left| {\overrightarrow {AB} } \right|cos\left( {\overrightarrow {SA} ,\overrightarrow {AB} } \right) = a \cdot a.cos\left( {{{180}^0} – \widehat {SAB}} \right)$
$ = {a^2}.cos\left( {{{180}^0} – {{60}^0}} \right) = {a^2} \cdot \cos {120^\circ } = – \frac{{{a^2}}}{2}$
+ $\overrightarrow {AC} \cdot \overrightarrow {AB} = 0$ ( Do tam giác $ABC$ vuông tại $A$ vì $B{C^2} = A{C^2} + A{B^2}$)
Suy ra $\cos (\overrightarrow {SC} ,\overrightarrow {AB} ) = \frac{{ – \frac{{{a^2}}}{2} + 0}}{{{a^2}}} = – \frac{1}{2}$.
Vậy $(\overrightarrow {SC} ,\overrightarrow {AB} ) = {120^\circ }$.
Câu 4. Cho tứ diện $ABCD$. Hai điểm $M$ và $N$ theo thứ tự là trung điểm của $BC$ và $AD$. Cho biết $AB = 10,CD = 6,MN = 7$. Tính góc giữa hai vectơ $\overrightarrow {AB} $ và $\overrightarrow {DC} $.
Lời giải
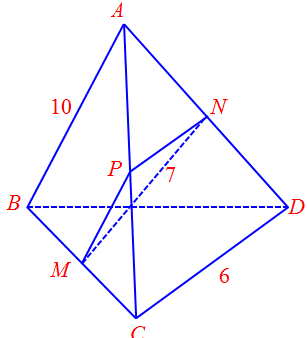
Ta có:
+ $\cos \left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) = \cos \left( {\overrightarrow {PM} ,\overrightarrow {NP} } \right) = \frac{{\overrightarrow {PM} \cdot \overrightarrow {NP} }}{{|\overrightarrow {PM} | \cdot |\overrightarrow {NP} |}}$
+ $\overrightarrow {PM} .\overrightarrow {NP} = \left| {\overrightarrow {PM} } \right| \cdot \left| {\overrightarrow {NP} } \right|cos\left( {\overrightarrow {PM} ,\overrightarrow {NP} } \right) = 5.3.cos\left( {{{180}^0} – \widehat {MPN}} \right)$
$ = – 15cos\widehat {MPN} = – 15.\frac{{P{M^2} + P{N^2} – M{N^2}}}{{2PM.PN}}$
$ = – 15.\frac{{{5^2} + {3^2} – {7^2}}}{{2.5.3}} = \frac{{15}}{2}$.
+ $|\overrightarrow {PM} | \cdot |\overrightarrow {NP} | = 5.3 = 15$
Suy ra $\cos \left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) = \cos \left( {\overrightarrow {PM} ,\overrightarrow {NP} } \right) = \frac{{\frac{{15}}{2}}}{{15}} = \frac{1}{2}$
Vậy $\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) = {60^0}$
Câu 5. Cho tứ diện $ABCD$. Tìm giá trị của k thỏa mãn: $\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = k$
Lời giải
Ta có:
$\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right).\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} – \overrightarrow {AD} .\overrightarrow {CB} $
$ = \overrightarrow {AC} \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right) + \overrightarrow {CB} \left( {\overrightarrow {CD} – \overrightarrow {AD} } \right) = \overrightarrow {AC} .\overrightarrow {CB} + \overrightarrow {CB} .\overrightarrow {AC} = 0.$
Vậy $k = 0$
Câu 6. Trong các kết quả sau đây, kết quả nào đúng? Cho hình lập phương $ABC.A’B’C’$ có cạnh$a$. Ta có$\overrightarrow {AB} .\overrightarrow {EG} $ bằng bao nhiêu?
Lời giải
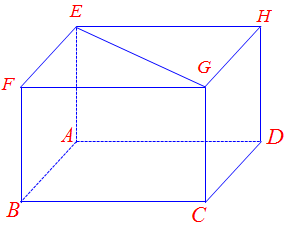
Ta có:
$\overrightarrow {AB} .\overrightarrow {EG} = \left( {\overrightarrow {EF} + \overrightarrow {EH} } \right)\left( {\overrightarrow {AE} + \overrightarrow {EF} + \overrightarrow {FB} } \right)$
$ = \overrightarrow {EF} .\overrightarrow {AE} + E{F^2} + \overrightarrow {EF} .\overrightarrow {FB} + \overrightarrow {EH} .\overrightarrow {AE} + \overrightarrow {EH} .\overrightarrow {EF} + \overrightarrow {EH} .\overrightarrow {FB} $
$ = 0 + {a^2} + 0 + 0 + 0 + \overrightarrow {EH} .\overrightarrow {EA} = {a^2} + 0 = {a^2}$
Vậy $\overrightarrow {AB} .\overrightarrow {EG} = {a^2}$.
DẠNG 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
Câu 7. Cho 2 vectơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn $\left| {\overrightarrow a } \right| = 4,\left| {\overrightarrow b } \right| = 3$ và $\left| {\overrightarrow a + 2\overrightarrow b } \right| = 2\sqrt 7 .$ Tính $\left( {\overrightarrow a ,\overrightarrow b } \right)$.
Lời giải
Ta có:
$\left| {\overrightarrow a + 2\overrightarrow b } \right| = 2\sqrt 7 $
$ \Leftrightarrow {\left( {\overrightarrow a + 2\overrightarrow b } \right)^2} = 28$
$ \Leftrightarrow {\overrightarrow a ^2} + 4{\overrightarrow b ^2} + 4\overrightarrow a \overrightarrow b = 28$
$ \Leftrightarrow {\left| {\overrightarrow a } \right|^2} + 4{\left| {\overrightarrow b } \right|^2} + 4\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|cos\left( {\overrightarrow a ,\overrightarrow b } \right) = 28$ $cos\left( {\overrightarrow a ,\overrightarrow b } \right) = – \frac{1}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^0}$
Vậy $\left( {\overrightarrow a ,\overrightarrow b } \right) = {120^0}$.
Câu 8. Cho $\left| {\overrightarrow a } \right| = 4,\,\left| {\overrightarrow b } \right| = 7$, góc giữa $\vec a$ và $\overrightarrow b $ bằng $60^\circ $. Biết $\left| {\overrightarrow a + 2\overrightarrow b } \right| = \sqrt m $ với $m$ nguyên dương. Tìm $m$.
Lời giải
Ta có: ${\left| {\overrightarrow a + 2\overrightarrow b } \right|^2} = {\left( {\overrightarrow a + 2\overrightarrow b } \right)^2} = {\left| {\overrightarrow a } \right|^2} + 4{\left| {\overrightarrow b } \right|^2} + 4\overrightarrow a .\overrightarrow b $
$ = {\left| {\overrightarrow a } \right|^2} + 4{\left| {\overrightarrow b } \right|^2} + 4\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|cos\left( {\overrightarrow a .\overrightarrow b } \right) = 16 + 4.49 + 4.4.7.\left( {\frac{1}{2}} \right) = 268$
$ \Rightarrow \left| {\overrightarrow a + 2\overrightarrow b } \right| = \sqrt {268} $
Vậy $m = 268$.
Câu 9. Cho ba vectơ $\vec a,\vec b,\vec c$ thóa mãn $|\vec a| = 1,|\vec b| = 2,|\vec a – \vec b| = 3$. Tính $(\vec a – 2\vec b) \cdot (2\vec a + \vec b)$.
Lời giải
Đáp án: $(\vec a – 2\vec b)(\vec a + 2\vec b) = 0$.
Ta có: $|\vec a – \vec b| = 3 \Leftrightarrow {(\vec a)^2} – 2 \cdot \vec a \cdot \vec b + {(\vec b)^2} = 9$
$ \Leftrightarrow 1 – 2 \cdot \vec a \cdot \vec b + 4 = 9 \Leftrightarrow \vec a \cdot \vec b = – 2$.
Suy ra $(\vec a – 2\vec b) \cdot (2\vec a + \vec b) = 2{(\vec a)^2} – 3 \cdot \vec a \cdot \vec b – 2{(\vec b)^2}$
$ = 2 \cdot 1 – 3 \cdot ( – 2) – 2 \cdot 4 = 0$.
Vậy $(\vec a – 2\vec b)(\vec a + 2\vec b) = 0$.
Câu 10. Cho hai vectơ $\overrightarrow a ,\overrightarrow b $ có $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1$ và $\left( {\overrightarrow a ,\overrightarrow b } \right) = {60^0}.$ Gọi ${x_1},\,{x_2}$ là các giá trị của $x$ thỏa mãn $\left| {x\overrightarrow a + \overrightarrow b } \right| = \sqrt 3 $. Tính ${x_1}^7 + {x_2}^7$.
Lời giải
Ta có:
$\left| {x\overrightarrow a + \overrightarrow b } \right| = \sqrt 3 \Leftrightarrow {\left( {x\overrightarrow a + \overrightarrow b } \right)^2} = 3$
$ \Leftrightarrow {x^2}{\overrightarrow a ^2} + 2x\overrightarrow a \overrightarrow b + {\overrightarrow b ^2} = 3$
$ \Leftrightarrow {x^2} + 2xcos{60^0} + 1 = 3$
$ \Leftrightarrow {x^2} + x – 2 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = – 2 \hfill \\
\end{gathered} \right.$
Vậy ${x_1}^7 + {x_2}^7 = {1^7} + {( – 2)^7} = – 127$.
Câu 11. Cho ba vectơ $\vec a,\vec b,\vec c$ thóa mãn: $|\vec a| = 4,|\vec b| = 1,|\vec c| = 5$ và $5(\vec b – \vec a) + 3\vec c = \vec 0$. Khi đó biểu thức $M = \vec a \cdot \vec b + \vec b \cdot \vec c + \vec c \cdot \vec a$ có giá trị bao nhiêu?
Lời giải
Ta có $5(\vec b – \vec a) + 3\vec c = \vec 0 \Leftrightarrow 5(\vec a – \vec b) = 3\vec c$
$ \Leftrightarrow 25{(\vec a – \vec b)^2} = 9{\vec c^2}$
$ \Leftrightarrow 25\left( {{{\vec a}^2} – 2\vec a\vec b + {{\vec b}^2}} \right) = 9{\vec c^2} \Leftrightarrow \vec a\vec b = 4.$
Tương tư: $5(\vec b – \vec a) + 3\vec c = \vec 0$
$ \Leftrightarrow 5\vec a = 5\vec b + 3\vec c \Leftrightarrow \vec b \cdot \vec c = 5$.
$5(\vec b – \vec a) + 3\vec c = \vec 0 \Leftrightarrow 5\vec b = 5\vec a – 3\vec c \Leftrightarrow \vec a \cdot \vec c = 20. $
Vậy $M = 4 + 5 + 20 = 29$.
Câu 12. Cho hai véc tơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn các điều kiện $\left| {\overrightarrow a } \right| = \frac{1}{2}\left| {\overrightarrow b } \right| = 1$,$\left| {\overrightarrow a – 2\overrightarrow b } \right| = \sqrt {15} $. Đặt $\overrightarrow u = \overrightarrow a + \overrightarrow b $ và $\overrightarrow v = 2k\overrightarrow a – \overrightarrow b $, $k \in \mathbb{R}$. Gọi $k$ là giá trị sao cho $\left( {\overrightarrow u ,\overrightarrow v } \right) = 60^\circ $. Biết $k = x + \frac{{3\sqrt y }}{2}$. Tính $5x + 4y$.
Lời giải
Ta có:
+ $\left| {\overrightarrow a – 2\overrightarrow b } \right| = \sqrt {15} \Leftrightarrow {\left| {\overrightarrow a } \right|^2} + 4{\left| {\overrightarrow b } \right|^2} – 4\overrightarrow a \overrightarrow b = 15 \Leftrightarrow 2\overrightarrow a \overrightarrow b = 1$.
+ $\overrightarrow u \overrightarrow v = \left( {\overrightarrow a + \overrightarrow b } \right)\left( {2k\overrightarrow a – \overrightarrow b } \right) = 2k{\left| {\overrightarrow a } \right|^2} – {\left| {\overrightarrow b } \right|^2} + \left( {2k – 1} \right)\overrightarrow a \overrightarrow b $
$ = 2k – 4 + \frac{{2k – 1}}{2}$.
+ ${\left( {\left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right|} \right)^2} = {\left( {\left| {\left( {\overrightarrow a + \overrightarrow b } \right)} \right|\left| {\left( {2k\overrightarrow a – \overrightarrow b } \right)} \right|} \right)^2}$
$ = \left( {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} + 2\overrightarrow a \overrightarrow b } \right)\left( {4{k^2}{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} – 4k\overrightarrow a \overrightarrow b } \right)$
$ = \left( {5 + 2\overrightarrow a \overrightarrow b } \right)\left( {4{k^2} + 4 – 4k\overrightarrow a \overrightarrow b } \right)$$ = 6\left( {4{k^2} + 4 – 2k} \right)$
$ \Rightarrow \left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right| = \sqrt {6\left( {4{k^2} + 4 – 2k} \right)} $.
Suy ra $\left( {\overrightarrow u ,\overrightarrow v } \right) = 60^\circ $$ \Rightarrow \cos \left( {60^\circ } \right) = \frac{{\overrightarrow u \overrightarrow v }}{{\left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right|}}$$ \Leftrightarrow \frac{1}{2} = \frac{{2k – 4 + \frac{{2k – 1}}{2}}}{{\sqrt {6\left( {4{k^2} + 4 – 2k} \right)} }}$$ \Leftrightarrow \sqrt {6\left( {4{k^2} + 4 – 2k} \right)} = 6k – 9$
$ \Leftrightarrow \sqrt {6\left( {4{k^2} + 4 – 2k} \right)} = 6k – 9$$ \Rightarrow 6\left( {4{k^2} + 2 – k} \right) = {\left( {6k – 9} \right)^2}$
$ \Leftrightarrow 12{k^2} – 96k + 57 = 0$$ \Leftrightarrow k = 4 \pm \frac{{3\sqrt 5 }}{2}$$ \Leftrightarrow k = 4 + \frac{{3\sqrt 5 }}{2}$ (thỏa phương trình)
Vậy $5x + 4y = 5.4 + 4.5 = 40$.
———-