■Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện – CD

1.1. Góc giữa đường thẳng và mặt phẳng

Định nghĩa

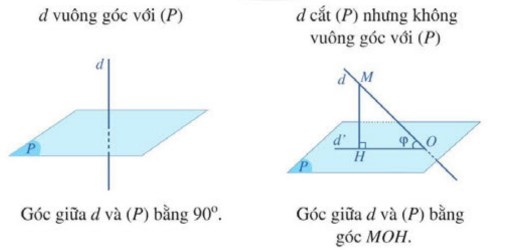
Cho đường thẳng d và mặt phẳng (P), ta có:  – Nếu đường thẳng d vuông góc với mặt phẳng (P) thì góc giữa d và (P) bằng \({{90}^{0}}\).  – Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d’ của đường thẳng d trên (P).

 

 

1.2. Góc nhị diện

a. Khái niệm

Một đường thẳng nằm trong một mặt phẳng chia mặt phẳng đó thành hai phần, mỗi phần được gọi là một nửa mặt phẳng và đường thẳng đó được gọi là bờ của mỗi nửa mặt phẳng này.

Khái niệm

Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.

 

Chú ý: Góc nhị diện còn được kí hiệu là [M, d, N] với M, N lần lượt là các điểm thuộc các nửa mặt phẳng (P), (Q) nhưng không thuộc đường thẳng d.

 

b. Số đo của góc nhị diện

Định nghĩa

Trong không gian, cho góc nhị diện.  – Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuộc hai mặt nhị diện và cùng vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.  – Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.  – Nếu số đo góc phẳng nhị diện bằng 90° thì góc nhị diện đó gọi là góc nhị diện vuông.

 

 

Chú ý: Số đo của góc nhị diện từ 0^o đến 180^o.

Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, \(SA = a\sqrt 6\). Tính sin của góc:

a) SC và (SAB).

b) AC và (SBC).

 

Hướng dẫn giải

 

a) Ta có: \(BC \bot AB{\rm{ (gt)}}\).

\(SA \bot BC\) (Vì \(SA \bot (ABCD)\))

Suy ra: \(BC \bot (SAB).\)

Do đó: SB là hình chiếu vuông góc của SC trên mặt phẳng (SAB).

\(\Rightarrow (SC,(SAB)) = \widehat {BSC}.\)

Ta có: \(\sin (SC,(SAB)) = \sin \widehat {BSC} = \frac{{BC}}{{SC}} = \frac{a}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{\sqrt 2 }}{4}\).

b) Trong  mặt phẳng (SAB) kẻ: \(AH \bot SB{\rm{ (H}} \in {\rm{SB)}}.\)

Theo câu a ta có: \(BC \bot (SAB) \Rightarrow AH \bot BC\) nên \(AH \bot (SBC)\) hay CH là hình chiếu vuông góc của AC trên mặt phẳng (SBC).

\(\Rightarrow (AC,(SBC)) = \widehat {ACH}.\)

Xét tam giác vuông SAB có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{S{A^2}}} = \frac{7}{{6{a^2}}} \Rightarrow AH = a.\sqrt {\frac{6}{7}} .\)

Vậy: \(\sin (AC,(SBC)) = \sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{{\sqrt {21} }}{7}.\)