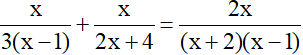Tài liệu Bộ đề thi Toán lớp 8 Giữa học kì 2 có đáp án năm 2023 gồm 20 đề thi tổng hợp từ đề thi môn Toán 8 của các trường THCS trên cả nước đã được biên soạn đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Giữa học kì 2 Toán lớp 8. Mời các bạn cùng đón xem:
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 1
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 1)
I. Trắc nghiệm (2 điểm): Khoanh tròn vào chữ cái đặt trước trả lời đúng.
Câu 1. Điều kiện xác định của phương trình :


A. x ≠ 1
B. x ≠ 1 và x ≠ −2
C. x ≠ −2
D. x ≠ 1 và x ≠ 2.
Câu 2. x = −2 là nghiệm của phương trình:


Câu 3. Phương trình 12 – 6x = 5x + 1 có nghiệm là:
A. 2
B. 4
C. 1
D. vô nghiệm.
Câu 4: Trong hình vẽ, biết: MN // BC, suy ra:




Câu 5. Cho ∆ABC có AD là phân giác của góc BAC,D ∈ BC . Biết AB = 6 cm; AC = 15 cm. Khi đó
 bằng:
bằng:


Câu 6. Cho ∆ABC đồng dạng với ∆HIK theo tỷ số đồng dạng k, ∆HIK đồng dạng với ∆DEF theo tỷ số đồng dạng m. ∆DEF đồng dạng với ∆ABC theo tỷ số đồng dạng là:


II. Tự luận:
Bài 1 (2,5 điểm): Giải các phương trình sau:


Bài 2 (2 điểm): Trong một buổi lao động, lớp 8A gồm 40 học sinh chia thành hai tốp: tốp thứ nhất trồng cây và tốp thứ hai làm vệ sinh. Tốp trồng cây đông hơn tốp làm vệ sinh là 8 người. Hỏi tốp trồng cây có bao nhiêu học sinh.
Bài 3 (3 điểm): Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD, phân giác của BCD cắt BD ở E.
a) Chứng minh: Tam giác AHB đồng dạng tam giác BCD.
b) Chứng minh AH.ED = HB.EB.
c) Tính diện tích tứ giác AECH.
Bài 4 (0,5 điểm): Chứng minh với mọi m, n ta có:


Đáp án
I. Trắc nghiệm (2 điểm):
Câu 1. Điều kiện xác định của phương trình là:


A. x ≠ 1
B. x ≠ 1 và x ≠ −2
C. x ≠ −2
D. x ≠ 1 và x ≠ 2
Giải thích:
Điều kiện xác định:


Vậy chọn B.
Câu 2. x = −2 là nghiệm của phương trình:


Giải thích:
– Xét phương trình (x2 + 1)(x + 2) = 0.
Thay x = −2 vào biểu thức (x2 + 1)(x + 2), ta được:
[(−2)2 + 1].(−2 + 2) = [(−2)2 + 1].0 = 0.
Do đó x = −2 là nghiệm của phương trình (x2 + 1)(x + 2) = 0.
– Xét phương trình:


ĐKXĐ: x ≠ ± 2
Ta thấy x = −2 (không TM ĐKXĐ) nên x = −2 không phải là nghiệm của phương trình :


– Xét phương trình 2x2 + 7x + 6 = 0.
Thay x = −2 vào biểu thức 2x2 + 7x + 6, ta được:
2.(−2)2 + 7.(−2) + 6 = 8 −14 + 6 = −6 + 6 = 0.
Do đó x = −2 là nghiệm của phương trình 2x2 + 7x + 6 = 0.
– Xét phương trình:


ĐKXĐ: x ≠ −2.
Ta thấy x = −2 (không TM ĐKXĐ) nên x = −2 không phải là nghiệm của phương trình


Từ đó suy ra: x = −2 là nghiệm của các phương trình (x2 + 1)(x + 2) = 0 và 2x2 + 7x + 6 = 0.
Vậy chọn A và C.
Câu 3. Phương trình 12 – 6x = 5x + 1 có nghiệm là:
A. 2
B. 4
C. 1
D. vô nghiệm.
Giải thích:


Do đó x = 1 là nghiệm của phương trình 12 – 6x = 5x + 1.
Vậy chọn C.
Câu 4: Trong hình vẽ, biết: MN // BC, suy ra:




Giải thích:
Ta có MN // BC, áp dụng định lý Ta-lét, ta có:


Vậy chọn D.
Câu 5. Cho ∆ABC có AD là phân giác của góc BAC, D ∈ BC . Biết AB = 6 cm; AC = 15 cm. Khi đó bằng:




Giải thích:


Trong ∆ABC có AD là phân giác của góc BAC.
Áp dụng tính chất đường phân giác của tam giác, ta được: .


Vậy chọn C.
Câu 6. Cho ∆ABC đồng dạng với ∆HIK theo tỷ số đồng dạng k, ∆HIK đồng dạng với ∆DEF theo tỷ số đồng dạng m. ∆DEF đồng dạng với ∆ABC theo tỷ số đồng dạng là:


Giải thích:


Vậy chọn C.
II. Tự luận:
Bài 1 (2,5 điểm):
a)


Vậy tập nghiệm của phương trình đã cho là:


b)
(2x − 3)(x2 − 1) = 0
<=>(2x − 3)(x + 1)(x – 1) = 0
<=>2x – 3 = 0 hoặc x + 1 = 0 hoặc x – 1 = 0


Vậy tập nghiệm của phương trình đã cho là:


c)


ĐKXĐ: x ≠ –1; x ≠ 2.


Suy ra: 2(x – 2) – (x + 1) = 2x – 11
2x – 4 – x – 1 = 2x – 11
x – 5 = 2x – 11
2x – x = 11 – 5
x = 6 (TMĐK).
Vậy tập nghiệm của phương trình đã cho là S = .
Bài 2 (2 điểm):
Gọi số học sinh tốp trồng cây là x (học sinh) ( x ∈ N, 8 < x < 40 ) .
Số học sinh tốp trồng cây đông hơn tốp làm vệ sinh là 8 người nên:
Số học sinh tốp làm vệ sinh là: x – 8 (học sinh).
Tổng số học sinh lớp 8A là 40 học sinh nên ta có phương trình:
x + x – 8 = 40
<=> 2x = 48
<=> x = 24 (TM)
Vậy tốp trồng cây có 24 học sinh.
Bài 3 (3 điểm):


|
GT |
Hình chữ nhật ABCD có AB = 8cm, BC = 6cm. AH ⊥ BD ( H ∈ BD) CE là tia phân giác góc BCD ( E ∈ BD ). |
|
KL |
a) ∆AHB đồng dạng ∆BCD. b) AH.ED = HB.EB.
|
a) Vì ABCD là hình chữ nhật nên AB // CD.
Suy ra (hai góc so le trong).


b)


c)
Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta được:
AB2 + AD2 = BC2


Áp dụng định lý Py-ta-go vào ∆ADH vuông tại H, ta được:


Bài 4 (0,5 điểm):
Giả sử


Vậy giả sử đúng, từ đó ta có điều phải chứng minh.
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 2
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 2)
I. Trắc nghiệm (2 điểm): Khoanh tròn vào chữ cái đặt trước trả lời đúng.
Câu 1: Số nghiệm của phương trình (x – 4)(x – 3)(x + 2) = 0 là:
A. Vô nghiệm
B. 2
C. 3
D. 4
Câu 2: Điều kiện xác định của phương trình là:




Câu 3: Phương trình vô nghiệm có tập nghiệm là:


Câu 4: Cho ΔMNP ,EF//MP ,E ∈ MN , F ∈ NP, ta có :


Câu 5: Trong hình vẽ, biết góc BAD = góc DAC , theo tính chất đường phân giác của tam giác thì tỉ lệ thức nào sau đây là đúng?




Câu 6: Biết 
 và CD = 10 cm. Vậy độ dài đoạn thẳng AB là:
và CD = 10 cm. Vậy độ dài đoạn thẳng AB là:
A. 4 cm
B. 50 cm
C. 25 cm
D. 20 cm.
II. Tự luận:
Bài 1 (2,5 điểm): Giải các phương trình sau:


Bài 2 (2 điểm): Một xe khách và một xe tải xuất phát cùng một lúc đi từ tỉnh A đến tỉnh B. Mỗi giờ xe khách chạy nhanh hơn xe tải là 5km nên xe khách đến B trước xe tải 30 phút. Tính quãng đường AB, biết rằng vận tốc của xe tải là 40 km/h.
Bài 3 (3 điểm): Cho tam giác ABC vuông ở A, AB = 6, AC = 8; đường cao AH, phân giác BD. Gọi I là giao điểm của AH và BD.
a) Tính AD, DC.
b) Chứng minh 
 .
.
c) Chứng minh AB.BI = BD.HB và tam giác AID cân.
Bài 4 (0,5 điểm): Giải phương trình:


Đáp án
I. Trắc nghiệm (2 điểm):
Câu 1: Số nghiệm của phương trình (x – 4)(x – 3)(x + 2) = 0 là:
A. Vô nghiệm
B. 2
C. 3
D. 4
Giải thích:
Ta có: (x – 4)(x – 3)(x + 2) = 0
x – 4 = 0 hoặc x – 3 = 0 hoặc x + 2 = 0
x = 4 hoặc x = 3 hoặc x = –2.
Do đó phương trình đã cho có 3 nghiệm x = 4; x = 3; x = –2.
Vậy chọn C.
Câu 2: Điều kiện xác định của phương trình là:


A. x ≠ 2 và
B. x ≠ −2 và
C. x ≠ −2 và x ≠ 3
D. x ≠ 2 và .
Giải thích:
ĐKXĐ:


Vậy chọn B.
Câu 3: Phương trình vô nghiệm có tập nghiệm là:


Giải thích:
Phương trình vô nghiệm có tập nghiệm là: S bằng rỗng
Vậy chọn A.
Câu 4:Cho ΔMNP ,EF//MP ,E ∈ MN , F ∈ NP, ta có :


Giải thích:


∆MNP có EF // MP, áp dụng định lý Ta-let, ta có:


Vậy chọn C.
Câu 5: Trong hình vẽ, biết góc BAD = góc DAC , theo tính chất đường phân giác của tam giác thì tỉ lệ thức nào sau đây là đúng?




Giải thích:
Vì góc BAD = góc DAC nên AD là tia phân giác góc BAC.
Áp dụng tính chất đường phân giác của tam giác, ta có:


Vậy chọn C.
Câu 6: Biết AB/CD =2/5 và CD = 10 cm. Vậy độ dài đoạn thẳng AB là:
A. 4 cm
B. 50 cm
C. 25 cm
D. 20 cm.
Giải thích:


Vậy chọn A.
II. Tự luận:
Bài 1 (2,5 điểm):
a) 3x − 12 = 0
<=> 3x = 12
<=> x = 4.
Vậy tập nghiệm của phương trình là S = .
b) (x – 2)(2x + 3) = 0
<=> x – 2 = 0 hoặc 2x + 3 = 0
<=> x = 2
hoặc


Vậy tập nghiệm của phương trình là:


c)


ĐKXĐ: x ≠ ± 2.


=>(x + 2)2 – 6(x – 2) = x2
<=>x2 + 4x + 4 – 6x + 12 = x2
<=>2x = 16
<=>x = 8 (TM ĐKXĐ)
Vậy tập nghiệm của phương trình là: S =
Bài 2 (2 điểm):
Đổi 30 phút = 
 giờ.
giờ.
Gọi chiều dài quãng đường AB là (km) ( ĐK: x > 0).
Thời gian xe khách đi từ A đến B là 
 giờ.
giờ.
Thời gian xe tải đi từ A đến B là 
 giờ.
giờ.
Theo bài ra, ta có phương trình:


Vậy quãng đường AB dài 180 km.
Bài 3 (3 điểm):




a) Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:


b)


c)


Bài 4 (0,5 điểm):
Ta có:
x2 + 9x + 20 = (x + 4)(x + 5);
x2 + 11x + 30 = (x + 6)(x + 5);
x2 + 13x + 42 = (x + 6)(x + 7).
ĐKXĐ: x ≠ − 4; x ≠ − 5; x ≠ − 6; x ≠ − 7.
Phương trình đã cho trở thành:


=>18(x + 7) − 18(x + 4) = (x + 7)(x + 4)
=>18(x + 7 − x − 4) = x2 + 11x + 28
=>x2 + 11x + 28 = 54
=>x2 + 11x − 26 = 0
=>x2 − 2x + 13x − 26 = 0
=>x(x – 2) + 13(x – 2) = 0
=>(x + 13)(x − 2) = 0
=>x + 13 = 0 hoặc x − 2 = 0
=> x = −13 (TM) hoặc x = 2 (TM).
Vậy tập nghiệm của phương trình đã cho là S = {−13; 2}.
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 3
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 3)
Bài 1 (2,5 điểm): Cho biểu thức:


Bài 2 (2 điểm): Giải toán bằng cách lập phương trình:
Lúc 6 giờ sáng một ô tô khởi thành từ A để đi đến B. Đến 7 giờ 30 phút một ô tô thứ hai cũng khởi hành từ A để đi đến B với vận tốc lớn hơn vận tốc ô tô thứ nhất là 20km/h và hai xe gặp nhau lúc 10 giờ 30 phút. Tính vận tốc mỗi ô tô? (ô tô không bị hư hỏng hay dừng lại dọc đường).
Bài 3 (1,5 điểm): Giải các phương trình sau:


Bài 4 (3 điểm): Cho hình bình hành ABCD, đường chéo lớn BD. Qua A kẻ đường thẳng cắt các đoạn thẳng BD, BC lần lượt tại E và F, cắt DC tại K.


Bài 4 (1 điểm): Cho a, b, c đôi một khác nhau và:


Tính P:


Đáp án
Bài 1 (2,5 điểm): Cho biểu thức:


a) Rút gọn P. Với x ≠ 3, x ≠ −3, x ≠ −7.




b) Ta có |x – 1| = 2.
<=>x – 1 = 2 hoặc x – 1 = – 2
<=>x = 3 (loại) hoặc x = – 1 (TM).
Thay x = – 1 vào P, ta được:


c) Ta có :


<=> (x – 3)(x + 5) = −12
<=> x2 + 2x – 15 = −12
<=> x2 + 2x – 3 = 0
<=> x2 – x + 3x – 3 = 0
<=> x(x – 1) + 3(x – 1) = 0
<=> (x – 1)(x + 3) = 0
<=> x – 1 = 0 hoặc x + 3 = 0
<=> x = 1 (TM) hoặc x = – 3 (loại).


Bài 2 (2 điểm):
Gọi vận tốc của ô tô thứ nhất là x (km/h) (ĐK: x > 0)
Vận tốc của ô tô thứ hai lớn hơn vận tốc của ô tô thứ nhất là 20km/h, nên vận tốc của ô tô thứ hai là: x + 20 (km/h).
Đến khi hai xe gặp nhau (lúc 10 giờ 30 phút):
– Thời gian đi của ô tô thứ nhất là:


– Thời gian đi của ô tô thứ hai là:
10 giờ 30 phút – 7 giờ 30 phút = 3 giờ.
Khi đó, quãng đường ô tô thứ nhất đi được:


Quãng đường ô tô thứ hai đi được:
3(x + 20) (km).
Theo đề bài, ta có phương trình:


Vậy vận tốc của ô tô thứ nhất là 40 (km/h);
Vận tốc của ô tô thứ hai là 40 + 20 = 60 (km/h).
Bài 3 (1,5 điểm):
a) 9x2 – 3 = (3x + 1)(2x – 3)
<=>9x2 – 3 = 6x2 – 7x – 3
<=>3x2 – 7x = 0
<=>x(3x – 7) = 0
<=> x = 0 hoặc 3x – 7 = 0


Vậy tập nghiệm của phương trình đã cho là:


b)


ĐK: x ≠ 0; x ≠ 5.
Phương trình đã cho tương đương:


<=> 3x2 + x – 5 = 4x + 3 + 3x(x – 5)
<=> 3x2 + x – 5 = 4x + 3 + 3x2 – 15x
<=> x – 5 = 4x + 3 – 15x
<=> 12x = 8


Vậy tập nghiệm của phương trình đã cho là:


Bài 4 (3 điểm):
|
GT |
Hình bình hành ABCD, đường chéo lớn BD. Qua A kẻ đường thẳng cắt BD, BC lần lượt tại E và F, cắt DC tại K. Kẻ AH ⊥ BD, BN ⊥ CD, BM ⊥ AD,(H ∈ BD,N ∈ CD,M ∈ AD) |
|
KL |
a) AE2 = EF.EK.
|


Vì ABCD là hình bình hành nên:
+ AD // BC hay AD // BF
+ AB // CD hay AB // DK.
Áp dụng định lý Ta-let, ta có:


Do đó AE2 = EF.EK (đpcm).
b) Xét ∆AHB và ∆BND có:


Mà AB = DC nên DC.DN = BD.BH (1)
Xét ∆ADH và ∆BDM có:


Từ (1) và (2) suy ra: AD.DM + DC.DN = BD.BH + DH.DB = BD.(BH + HD) = BD.BD = BD2.
Do đó AD.DM + DC.DN = BD2 (đpcm).
Bài 4 (1 điểm):
Ta có :


Ta thấy a2 + 2bc = a2 + bc + (–ab – ac) = a(a – b) – c(a – b) = (a – b)(a – c)
Tương tự, b2 + 2ac = (b – a)(b – c) ; c2 + 2ab = (c – a)(c – b).
Khi đó:


Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 4
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 4)
Bài 1 (2,5 điểm): Cho biểu thức:


a) Rút gọn A.
b) Tính giá trị của A khi x = −4.
c) Tính các giá trị nguyên của x để A có giá trị là số nguyên.
Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.
Một tàu chở hàng khởi hành từ Thành phố Hồ Chí Minh với vận tốc 36km/h. Sau đó 2 giờ một tàu chở khách cũng đi từ đó với vận tốc 48km/h đuổi theo tàu hàng. Hỏi tàu khách đi bao lâu thì gặp tàu hàng ?
Bài 3 (2 điểm): Giải các phương trình sau:


Bài 4 (3 điểm): Cho tam giác ABC vuông tại A. Vẽ đường thẳng d đi qua A và song song với đường thẳng BC, BH vuông góc với d tại H.
a) Chứng minh ∆ABC đồng dạng ∆HAB.
b) Gọi K là hình chiếu của C trên d. Chứng minh AH.AK = BH.CK.
c) Gọi M là giao điểm của hai đoạn thẳng AB và HC. Tính độ dài đoạn thẳng HA và diện tích ∆MBC, khi AB = 3cm, AC = 4cm, BC = 5cm.
Bài 5 (0,5 điểm): Tìm x, y thỏa mãn phương trình sau: x2 − 4x + y2 − 6y + 15 = 2.
Đáp án
Bài 1 (2,5 điểm):
a) ĐK: x ≠ ± 2.


b) Với x = −4 (TMĐK) thì:


c) Để A có giá trị là số nguyên hay :


Ta có bảng sau:
|
x – 2 |
–3 |
–1 |
1 |
3 |
|
x |
–1 (TM) |
1 (TM) |
3 (TM) |
5 (TM) |
Vậy để A có giá trị là số nguyên thì x thuộc {–1; 1; 3; 5}.
Bài 2 (2 điểm):
Gọi x (giờ) là thời gian tàu chở khách đi để đuổi kịp tàu hàng (x > 0).
Khi đó, quãng đường tàu chở khách đã đi được là 48x (km).
Vì tàu chở hàng chạy trước tàu chở khách 2 giờ, nên khi đó quãng đường tàu chở khách đã đi được là 36(x + 2) (km).
Theo đề bài, ta có phương trình:
<=>48x = 36(x + 2)
<=>48x = 36x + 72
<=>48x – 36x = 72
<=>12x = 72
<=>x = 6 (TMĐK).
Vậy tàu chở khách đi được 6 giờ thì đuổi kịp tàu chở hàng.
Bài 3 (2 điểm):
a)
2x(x − 2) + 5(x − 2) = 0
<=> (x − 2)(2x + 5) = 0
<=> x − 2 = 0 hoặc 2x + 5 = 0


Vậy tập nghiệm của phương trình đã cho là:


b)


<=> 3(3x − 4) = 2(4x + 1)
<=> 9x − 12 = 8x + 2
<=> 9x − 8x = 2 + 12
<=> x = 14
Vậy tập nghiệm của phương trình đã cho là : S = .
c)


ĐKXĐ: x ≠ 1; x ≠ − 1.
Phương trình đã cho tương đương:


=>2x(x + 1) − x(x − 1) = (x − 1)(x + 1)
<=> 2x2 + 2x − x2 + x = x2 – 1
<=> x2 + 3x = x2 – 1
<=> 3x = – 1


Vậy tập nghiệm của phương trình đã cho là:


Bài 4 (3 điểm):




a) Ta có


Nên:


Xét ∆ABC và ∆HAB có:


b) Ta có:


(vì K là hình chiếu của C trên d)


Lại có :


Xét ∆HAB và ∆KCA có:




c) Từ câu a:


Ta có AH // BC, áp dụng định lý Ta-let:


Lại có AM + BM = AB = 3 (cm).


Diện tích tam giác MBC là:


Bài 5 (0,5 điểm):
Ta có x2 − 4x + y2 − 6y + 15 = 2
Û x2 − 4x + 4 + y2 − 6y + 9 = 0
Û (x – 2)2 + (y – 3)2 = 0
Vì (x – 2)2 ≥ 0 và (y – 3)2 ≥ 0 nên:
Để (x – 2)2 + (y – 3)2 = 0 thì (x – 2)2 = 0 và (y – 3)2 = 0.
Khi đó, x – 2 = 0 và y – 3 = 0.
Do đó x = 2; y = 3.
Vậy để x, y thỏa mãn phương trình đã cho thì x = 2; y = 3.
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 5
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 5)
Bài 1 (2 điểm):
1) Tìm giá trị của m để phương trình 2x – m = 1 – x nhận giá trị x = –1 là nghiệm.
2) Rút gọn biểu thức :


Bài 2 (2 điểm): Giải bài toán bằng cách lập phương trình.
Một tổ sản xuất lập kế hoạch sản xuất một lô hàng, theo đó mỗi giờ phải làm 30 sản phẩm. Khi thực hiện, mỗi giờ tổ chỉ sản xuất được 27 sản phẩm, do đó tổ đã hoàn thành lô hàng chậm hơn so với dự kiến 1 giờ 10 phút. Hỏi số sản phẩm mà tổ sản xuất theo kế hoạch là bao nhiêu?
Bài 3 (2 điểm): Giải các phương trình:


Bài 3 (3 điểm): Cho hình chữ nhật ABCD có AB = 12 cm, AD = 9 cm. Gọi H là chân đường vuông góc kẻ từ A đến cạnh BD.
a) Chứng minh tam giác ADH đồng dạng với tam giác DBC và AD2 = HD.BD.
b) Tính độ dài HD và HB.
c) Tia phân giác của góc ADB cắt AH tại E và AB tại F. Chứng minh :


Bài 4 (1 điểm): Tìm giá trị lớn nhất của biểu thức A = 4x – 2x2 – |x3 – x2| + 7.
Đáp án
Bài 1 (2 điểm):
1) Thay x = –1 vào phương trình 2x – m = 1 – x, ta được:
2.(–1) – m = 1 – (–1)
<=> –2 – m = 2
<=> m = – 4.
Vậy để phương trình 2x – m = 1 – x nhận giá trị x = –1 là nghiệm thì m = – 4.
2) Với ĐKXĐ: x ≠ 1, x ≠ –1 và x ≠ 2, ta có :


Bài 2 (2 điểm):
Gọi số sản phẩm mà tổ sản xuất theo kế hoạch là x (sản phẩm) ()
Thời gian làm hết số sản phẩm theo kế hoạch là:


Thời gian làm hết số sản phẩm theo thực tế là:


Đổi 1 giờ 10 phút


Vì tổ đã hoàn thành lô hàng chậm hơn so với dự kiến 1 giờ 10 phút, nên ta có phương trình:


Vậy số sản phẩm mà tổ sản xuất theo kế hoạch là 315 sản phẩm.
Bài 3 (2 điểm):
a) 7 + 2x = 22 – 3x
<=> 2x + 3x = 22 – 7
<=> 5x = 15
<=> x = 3.
Vậy tập nghiệm của phương trình là S = .
b) 2x3 + 6x2 = x2 + 3x
<=> 2x2 (x + 3) = x(x + 3)
<=> 2x2 (x + 3) – x(x + 3) = 0
<=> x (x + 3)(2x – 1) = 0
<=> x = 0 hoặc x + 3 = 0 hoặc 2x – 1 = 0


Vậy tập nghiệm của phương trình đã cho là:


c)


ĐK: x ≠ ± 2
Phương trình đã cho tương đương:


=>(x – 2)2 – 3(x + 2) = 2(x – 11)
<=> x2 – 4x + 4 – 3x – 6 = 2x – 22
<=> x2 – 7x – 2 = 2x – 22
<=> x2 – 9x + 20 = 0
<=> (x2 – 4x) – (5x – 20) = 0
<=> x(x – 4) – 5(x – 4) = 0
<=> (x – 4)(x – 5) = 0
<=> x – 4 = 0 hoặc x – 5 = 0
<=> x = 4 hoặc x = 5.
Vậy tập nghiệm của phương trình đã cho là S = .
Bài 3 (3 điểm):




Ta có:


Tứ giác ABCD là hình chữ nhật nên AD // BD.


Xét ∆ADH và ∆DBC có:


Vậy ∆ADH đồng dạng ∆DBC và AD2 = HD.BD.
b) Áp dụng định lý Py-ta-go vào ∆ABD vuông tại A, ta có:
BD2 = AD2 + AB2 = 92 + 122 = 81 + 144 = 225
=> BD = 15 (cm).
Ta có AD2 = HD.BD


=> BH = BD – DH = 15 – 5,4 = 9,6 (cm).
Vậy DH = 5,4 cm; BH = 9,6 cm.
c) Xét ∆ADH có DE là tia phân giác của góc ADH
Áp dụng tính chất đường phân giác của tam giác, ta có:


Xét ∆ADB có DF là tia phân giác của góc ADB
Áp dụng tính chất đường phân giác của tam giác, ta có:


Bài 4 (1 điểm):
Ta có A = 4x – 2x2 – |x3 – x2| + 7
= – 2x2 + 4x – 2 – x2 |x – 1| + 9
= – 2(x2 – 2x + 1) – x2 |x – 1| + 9
= – 2(x – 1) 2 – x2 |x – 1| + 9
Vì (x – 1) 2 ≥ 0 nên – 2(x – 1) 2 ≤ 0.
Dấu “=” xảy ra khi x = 1.
Mặt khác, x2 ≥ 0 và |x – 1| ≥ 0 nên x2 |x – 1| ≥ 0 hay – x2 |x – 1| ≤ 0.
Dấu “=” xảy ra khi x = 1.
Do đó A ≤ 9.
Vậy giá trị lớn nhất của biểu thức A là 9 khi x = 1.
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 6
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 6)
Câu 1 (4 điểm) : Giải phương trình:
Câu 2 (2 điểm) : Giải bài toán bằng cách lập phương trình:
Một công nhân làm một số sản phẩm dự định trong 5 giờ xong. Lúc đầu mỗi giờ người đó làm được 12 sản phẩm. Sau khi làm được một nửa số lượng sản phẩm được giao, nhờ hợp lý hóa một số thao tác nên mỗi giờ người đó làm thêm được 3 sản phẩm nữa. Vì vậy người công nhân đó hoàn thành sớm hơn dự định 30 phút. Tính số lượng sản phẩm được giao.
Câu 3 (3,5 điểm) : Cho tam giác ABC có trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt AC ở E.
1) Chứng minh : DE // BC.
2) Gọi G là giao điểm AM với DE. Chứng minh G là trung điểm của DE. Tìm điều kiện của tam giác ABC để G là trung điểm của AM.
3) Gọi AN là phân giác của góc BAC, (N thuộc BC). Biết AB = 12cm, AC = 16cm, BC = 20cm. Tính diện tích tam giác AMN.
Câu 4 (0,5 điểm) : Tìm nghiệm của phương trình:
6x2 – 2xy = 3y – 11x + 2


Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 7
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 7)
Bài 1 (1,5 điểm) : Cho biểu thức
a) Rút gọn P
b) Tính giá trị của P tại
Bài 2 (3,0 điểm) : Giải các phương trình sau
Bài 3 (2,0 điểm) : Giải bài toán sau bằng cách lập phương trình
Lúc 7 giờ sáng một người đi xa máy chở hàng từ A đến B với vận tốc 50km/h. Khi đến B người đó giao hàng trong 15 phút rồi quay trở về A với vận tốc 40km/h. Biết rằng người đó về đến A llucs 9 giờ 30 phút, hãy tính độ dài quãng đường AB.
Bài 4 (3,0 điểm) : Cho ΔABC vuông tại A, biết AB = 21cm, AC = 28cm, phân giác AD (D ∈ BC)
a) Tính độ dài DB, DC
b) Gọi E là hình chiếu của D trên AC. Hãy tính độ dài DE, EC
c) Chứng minh ΔABC đồng dạng với ΔEDC . Tính tỉ số đồng dạng
d) Gọi I là giao điểm các đường phân giác và G là trọng tâm của ΔABC . Chứng minh rằng IG // AC.
Bài 5 (0,5 diểm) : Hãy giải và biện luận phương trình sau theo tham số m
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 8
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 8)
I. PHẦN TRẮC NGHIỆM (1,5 điểm). Chọn đáp án đúng
Câu 1 : Trong các phương trình sau đâu là phương trình bậc nhất một ẩn:
Câu 2 : Điều kiện xã định của phương trình là:
Câu 3 : Phương trình 2x2 – 2x = 0 có tập nghiệm là:
A. S = {0}
B. S = {0;1}
C. S = {-1;0}
D. S = {1}
Câu 4 : Phương trình 2y + m = y -1 nhận y = 3 là nghiệm khi m bằng:
A. 3
B. 4
C. – 4
D. 8
Câu 5 : Biết AD là tia phân giác góc A của ΔABC (D ∈ BC) và AB = 5cm; AC = 10cm; DC = 2cm Khi đó độ dài DB bằng
A. 1cm
B. 2cm
C. 3cm
D. 4cm
Câu 6 : Hai đường chéo của một hình thoi có độ dài là a và b thì diện tích của hình thoi là:
II. PHẦN TỰ LUẬN (8,5 điểm)
Bài 1 (2,5 điểm) : Giải phương trình
Bài 2 (2,5 điểm) : Cho biểu thức
a) Rút gọn biểu thức P
b) Tìm x nguyên để P có giá trị nguyên
Bài 3 (2 điểm) : Một người đi xe máy từ A đến B với vận tốc 30km/h. Khi đến B người đó nghỉ 10 phút rồi quay trở về A với vận tốc 35km/h. Tính quãng đường AB biết thời gian cả đi, về và nghỉ là 6 giờ 40 phút?
Bài 4 (3,5 điểm) : Cho ΔABC có , AB = 30cm , AC = 40cm đường cao AH; BD là phân giác của
; I là giao điểm của AH và BD.
a) Chứng minnh ΔABC đồng dạng với
b) Tính BD, DC
c) Chứng minh BD.IH = BI.AD và AI = AD
d) Chứng minh
Bài 5 (0,5 điểm) : Giải phương trình x(4x – 1)2 (2x – 1) = 9
………………………………
………………………………
………………………………
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 9
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 9)
I. Trắc nghiệm: Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Phương trình nào sau đây có nghiệm x = 3?
A. 2x – 4 = x + 1
B. 2x – 1 = x + 3
C. 2x + 1 = x + 4
D. x + 1 = 2x – 1
Câu 2: Phương trình 6 – 3x = 0 có nghiệm là:


Câu 3: Một hình thang có đáy lớn là 18 cm, chiều cao là 4 cm, diện tích là 60 cm2. Độ dài đáy nhỏ của hình thang đó là:
A. 9 cm
B. 6 cm
C. 12 cm
D. 15 cm
Câu 4: Số nghiệm của phương trình (2x – 2)(x – 3)(x2 – 2x + 2) = 0 là:
A. 3
B. 2
C. 1
D. 0.
Câu 5: Điều kiện xác định (ĐKXĐ) của phương trình:


A. x ≠ 5và x ≠ 7
B. x ≠ −5 và x ≠ −7
C. x ≠ −5 và x ≠ 3
D) x ≠ 3 và x ≠ −3.
Câu 6: Cho tam giác ABC có AB = 6 cm, AC = 8 cm và AD là đường phân giác trong của góc A. Tỉ số BD/CD bằng :


Câu 7: Cho ∆ABC đồng dạng với ∆MNP. Biết AB/MB = 1/5 và diện tích tam giác MNP là 25 cm2. Khi đó, diện tích tam giác ABC bằng:
A. 1 cm2
B. 5 cm2
C. 125 cm2
D. 625 cm2.
Câu 8: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’và C’D’ nếu có tỉ lệ thức:


II. Tự luận:
Bài 1: Giải các phương trình:


Bài 2: Giải bài toán sau bằng cách lập phương trình:
Một ô tô đi từ A đến B với vận tốc trung bình 50km/h. Lúc về, ô tô đi với vận tốc trung bình 60km/h, nên thời gian về ít hơn thời gian đi là 30 phút. Hỏi quãng đường AB dài bao nhiêu ki-lô-mét?
Bài 3: Cho tam giác ABC có trung tuyến AM, các tia phân giác của các góc AMB, AMC cắt AB, AC lần lượt ở D, E.
a) Chứng minh DE // BC.
b) Cho BC = 6 cm, AM = 5 cm. Tính DE?
c) Gọi I là giao điểm của AM và DE nếu tam giác ABC có BC cố định, AM không đổi thì điểm I chuyển động trên đường nào?
Bài 4: Cho x2 + y2 + z2 = 200. Tìm giá trị nhỏ nhất của biểu thức: M = 2xy – yz – zx.
Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 10
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 10)
I. Trắc nghiệm: Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
A. 3x +2 = 0
B. 0x + 7 = 0
C. 2x + y = 0
D. x2 + 9 = 0.
Câu 2: Số nghiệm của phương trình:


A. 3
B. 2
C. 0
D. 1.
Câu 3: Tập nghiệm của phương trình




Câu 4: Biết AB/CD = 2/5 và CD = 10 cm. Vậy độ dài đoạn thẳng AB là:
A. 4 cm
B. 50 cm
C. 25 cm
D. 20 cm.
Câu 5: Cho ∆ABC có MN // BC (M ∈ AB, N ∈ AC).


Theo hệ quả của định lí Ta-lét, ta có:


Câu 6: Diện tích hình thoi có độ dài hai đường chéo bằng 8 cm và 10 cm là:
A. 160 cm2
B. 80 cm2
C. 20 cm2
D. 40 cm2
Câu 7: Cho hình vẽ, biết AD là tia phân giác của góc BAC (D ∈ BC), AB = 3cm, AC = 5 cm. Khi đó tỉ số x/y bằng bao nhiêu?




Câu 8: Cho ∆ABC đồng dạng với ∆MNP theo tỉ số đồng dạng k = 3. Tỉ số chu vi của ∆ABC và ∆MNP là:
A. 1/3
B. 3
C. 9
D. 1,5.
II. Tự luận:
Bài 1: Giải các phương trình sau:


Bài 2: Số lúa ở kho thứ nhất gấp đôi số lúa ở kho thứ hai. Nếu bớt ở kho thứ nhất đi 750 tạ và thêm vào kho thứ hai 350 tạ thì số lúa ở trong hai kho sẽ bằng nhau. Tính khối lượng lúa lúc đầu mỗi kho.
Bài 3: Cho ∆ABC vuông tại A có đường cao AH (H ∈ BC).
a) Chứng minh ∆ABC đồng dạng ∆HAC.
b) Chứng minh ∆HBA đồng dạng ∆HAC. Từ đó suy ra: AH2 = BH.HC.
c) Kẻ đường phân giác BE của ∆ABC (E thuộc AC). Biết BH = 9cm, HC = 16cm. Tính độ dài các đoạn thẳng AE và EC.
d) Trong ∆AEB kẻ đường phân giác EM (M ∈ AB). Trong ∆BEC kẻ đường phân giác EN (N ∈ BC). Chứng minh:


Bài 4: Cho các số dương x, y thỏa mãn x + y = 1. Tìm giá trị nhỏ nhất của biểu thức:


Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 11
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 11)
I. Trắc nghiệm: Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Tập nghiệm của phương trình 2x − 6 = 0 là:
A. S =
B. S = {−3}
C. S =
D. S = {−4}
Câu 2: Điều kiện xác định của phương trình:




Câu 3: Nghiệm của phương trình:


A. x = 4
B. x = 2
C. x = −4
D. x = −2.
Câu 4: Cho biết AB/CD = 3/4 và CD = 12 cm. Tính AB.
A. AB = 6cm
B. AB = 5cm
C. AB = 8cm
D. AB = 9 cm.
Câu 5: Trong các số 1; 2; −2 và −3 thì số nào là nghiệm của phương trình x + 1 = 2x + 3 ?
A. x = 1
B. x = −2
C. x = 2
D. x = −3.
Câu 6: Trong vẽ dưới đây, biết NK // PQ. Theo hệ quả của định lí Ta-lét thì tỉ lệ thức nào sau đây là đúng?




Câu 7: Cho tam giác ABC đồng dạng tam giác DEF theo tỉ số đồng dạng k = 3/4 . Tỉ số chu vi của hai tam giác đó bằng:


Câu 8: AD là đường phân giác của góc A trong hình nào dưới đây?


A. Hình a


B. Hình b


C. Hình c


D. Hình d.
II. Tự luận:
Bài 1: Giải các phương trình sau:


Bài 2: Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phẩm. Khi thực hiện, mỗi ngày tổ sản xuất được 57 sản phẩm. Do đó tổ đã hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch, tổ phải sản xuất bao nhiêu sản phẩm?
Bài 3: Cho tam giác AOB có AB = 18 cm, OA = 12 cm, OB = 9 cm. Trên tia đối của tia OB lấy điểm D sao cho OD = 3 cm. Qua D kẻ đường thẳng song song với AB cắt tia AO ở C. Gọi F là giao điểm của AD và BC.
a) Tính độ dài OC và CD.
b) Chứng minh: FD.BC = FC.AD.
c) Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N. Chứng minh: OM = ON.
Bài 4: Cho (a + b + c)2 = a2 + b2 + c2 và a, b, c khác 0. Chứng minh:


Đề thi Toán lớp 8 Giữa kì 2 năm 2023 có đáp án (20 Đề) – Đề 12
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa kì 2
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài:90 phút
(không kể thời gian phát đề)
(Đề số 12)
I. Trắc nghiệm: Khoanh vào chữ cái đặt trước câu trả lời đúng.
Câu 1: Phương trình (x − 1)(x + 2) = 0 có tập nghiệm là?
A. S = {1; −2}
B. S = {−1; 2}
C. S = {1; 2}
D. S = {−1; −2}
Câu 2: Cho AB = 3cm, CD = 5cm. Tính AB/CD = ?


Câu 3: Phương trình 2x − 12 = 0 có nghiệm là:
A. x = −6
B. x = 6
C. x = −12
D. x = 12.
Câu 4: Tập nghiệm của phương trình (x – 3)(x + 1) = 0 là:
A. S = {−3; −1}
B. S =
C. S =
D. S = .
Câu 5: Cho các phương trình: x(2x + 5) = 0 (1); 2y + 3 = 2y − 3 (2); u2 + 2 = 0 (3); (3t + 1)(t − 1) = 0 (4).


Câu 6: Cho ∆ABC đồng dạng với ∆HIK theo tỷ số đồng dạng k = 2/3 . Chu vi tam giác ABC bằng 60 cm. Tính chu vi tam giác HIK:
A. 30 cm
B. 90 cm
C. 9 dm
D. 40 cm.
Câu 7: Cho hình vẽ dưới đây, tam giác ABC có AM là tia phân giác. Độ dài đoạn thẳng MB bằng:


A. 1,7
B. 2,8
C. 3,8
D. 5,1
Câu 8: Cho ∆ABC đồng dạng ∆MNP theo tỉ số đồng dạng là . Khi đó tỉ số hai đường cao tương ứng của ∆ABC và ∆MNP là:
A. 3
B. 49
C. 7
D. 14.
II. Tự luận:
Bài 1: Giải các phương trình:


Bài 2: Một số tự nhiên có hai chữ số. Chữ số hàng đơn vị gấp hai lần chữ số hàng chục. Nếu thêm chữ số 1 xen vào giữa hai chữ số đó thì được một số mới lớn hơn số ban đầu là 370. Tìm số ban đầu.
Bài 3: Cho hình bình hành ABCD có AB = 6 cm, AD = 8 cm. Trên cạnh CD lấy điểm E sao cho DE = 4 cm. Đường thẳng AE cắt BD tại O và cắt đường thẳng BC tại F.
a) Chứng minh: Tam giác ADE đồng dạng với tam giác FBA.
b) Tính OD/OB và BF.
c) Chứng minh: OA2 = OE.OF.
d) Gọi K là giao điểm của đường thẳng BE với DF. Tính FK/DK .
Bài 4: Giải phương trình: 8(x − 3)3 + x3 = 6x2 − 12x + 8.