Đề khảo sát chất lượng học kì II
Môn toán lớp 8
Phần I : Trắc nghiệm (3,0 điểm)
Hãy chọn chỉ 1 chữ cái đứng trước câu trả lời đúng.
Câu 1: Phương trình 5(x + 1) – 2 = 3x – 5 có nghiệm là giá trị nào dưới đây:
A. 1
B. – 4
C. 4
D. 1
Câu 2: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
A. -2x +3= 0
B. x2 +3x – 2=0
C. 0. x – 5 =0
D. x(2x – 1 )=0
Câu 3: Phương trình 3x (2x + 3) = 2(2x + 3) có tập nghiệm là:
A. \(S = {\rm{\{ }}\frac{3}{2};\frac{{ – 2}}{3}{\rm{\} }}\)
B. \(S = {\rm{\{ }}\frac{3}{2};\frac{2}{3}{\rm{\} }}\)
C. \(S = {\rm{\{ – }}\frac{3}{2};\frac{2}{3}{\rm{\} }}\)
D. S= { -1 ; 1}
Câu 4: Phương trình 2x+k= x-1 nhận x = 2 là nghiệm khi
A. k = 3
B. k =- 3
C. k = 0
D. k = 1
Câu 5: Điều kiện xác định của phương trình \(\frac{{5x + 3}}{{x – 2}} = \frac{{2x}}{{{x^2} – 4}} – \frac{{2x + 3}}{x}\) là:
A. \(x \ne 0;x \ne 2\)
B. \(x \ne 2;x \ne – 2\)
C. \(x \ne 0;x \ne – 2\)
D. \(x \ne 0;x \ne \pm 2\)
Câu 6: Nếu \(x \le y\)thì:
A. a>b
B. \(a \le b\)
C. a<b
D. \(a \ge b\)
Câu 8. x =1 là một nghiệm của bất phương trình
A. x+5 < -13
B. \(\frac{x}{2} + 1 > 5x\)
C. 4x – 1>3 + x
D. \(\frac{x}{3} + 1 > – x\)
Câu 9. Bất phương trình: \(\frac{{15x + 2}}{4} > 1 + 3x\) có nghiệm là:
A. x<1
B. x<2
C. x > 2
D. Một kết quả khác
Câu 10. Phương trình |2x+5| – 3= x có nghiệm là :
A. \[{\rm{\{ }} – 2;\frac{{13}}{3}{\rm{\} }}\]
B. \[{\rm{\{ }} – 2;\frac{{ – 157}}{3}{\rm{\} }}\]
C. \[{\rm{\{ }} – 2;\frac{8}{3}{\rm{\} }}\]
D. \[{\rm{\{ }} – 2; – \frac{8}{3}{\rm{\} }}\]
Câu 11. Tam giác ABC vuông tại A có độ dài hai cạnh góc vuông lần lượt là 4cm và 5cm. Diện tích của tam giác ABC là:
A. 10 cm2
B. 20 cm2
C. 34 cm2
D. 18 cm2
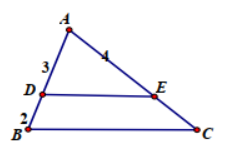
Câu 12. Cho hình vẽ biết DE // BC và độ dài các đoạn
thẳng như hình vẽ. Khi đó \(\frac{{AE}}{{EC}}\)bằng:


A. \(\frac{3}{2}\)
B. \(\frac{2}{3}\)
C. \(\frac{4}{5}\)
D. \(\frac{4}{3}\)
Câu 13. Cho ∆ABC có AB=14cm , AC=21 cm . AD là phân giác của góc A.
Biết BD = 8cm .Độ dài cạnh DC là :
A. 16/3cm
B. 12cm
C. 20 cm
D. 298/3 cm
Câu 14: Tam giác MNP đồng dạng với tam giác ABC theo tỉ số k = 1/ 2. Biết AB = 10BC = 14cm, độ dài đoạn thẳng là MN là
A. 7cm
B. 5cm
C. 28 cm
D. 20cm
Câu 15. Cho \(\Delta ABC\) và \(\Delta HIK\)có \(\frac{{AB}}{{IH}} = \frac{{AC}}{{HK}}\). Để \(\Delta ABC\) đồng dạng với \(\Delta HIK\) cần thêm điều kiện là:
A. \(\angle A = \angle I\)
B. \(\angle A = \angle H\)
C.\(\angle B = \angle I\)
D. \(\angle C = \angle K\)
Phần II : Tự luận (7,0 điểm)
Bài 1 (1 điểm): Giải các phương trình sau:
a) 3(x – 5) -2( 2x – 1) = 7 – 2x
b) \(\frac{2}{{x + 1}} – \frac{1}{{x – 2}} = \frac{{3x – 11}}{{(x + 1)(x – 2)}}\)
Bài 2 (1 điểm): Giải các phương trình sau:
a. Giải bất phương trình \(\frac{{3(x – 1)}}{4} + 1 \le \frac{{x + 2}}{3}\)
b. Cho \(A = \frac{{x – 5}}{{x – 8}}\). Tìm giá trị của x để A dương.
Bài 3 (1,5 điểm): Giải bài toán bằng cách lập phương trình.
Một phân số có tổng của tử và mẫu là 15. Nếu giảm tử đi 5 đơn vị và tăng mẫu thêm 2 đơn vị thì đươc phân số mới bằng 1/5. Tìm phân số ban đầu.
Bài 4 (3 điểm):
1. Cho tam giác ABC vuông ở A, AB = 6, AC = 8; đường cao AH, phân giác BD. Gọi I là giao điểm của AH và BD.
a. Tính AD, DC.
b. Chứng minh AB.BI = BD.HB và tam giác AID cân.
c. Chứng minh \(\frac{{IH}}{{IA}} = \frac{{AD}}{{DC}}\)
2. Một hình hộp chữ nhật có ba kích thước 3cm, 4cm và 6cm. Tính diện tích toàn phần của hình hộp chữ nhật.
Bài 5 (1 điểm): Tìm x; y thỏa mãn phương trình sau:
a) Cho a, b là các số dương. Chứng minh rằng:\(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\)
b) Cho a,b,c là độ dài 3 vạnh của một tam giác. Chứng minh rằng:
\(\frac{1}{{a + b – c}} + \frac{1}{{b + c – a}} + \frac{1}{{c + a – b}} \ge \frac{1}{a} + \frac{1}{b} + \frac{1}{c}\)
Trường THCS An Hòa
Đáp án đề KSCL học kì II
Môn toán 8 năm học 2018-2019
|
Câu |
Nội dung |
Điểm |
||||||||||||||||||||
|
I. Trắc nghiệm (3đ) |
|
0.2×15 |
||||||||||||||||||||
|
II. Tự luận Bài 1( 1 điểm) |
a. Biến đổi về dạng:
|
0.25×2 |
||||||||||||||||||||
|
b. – Tìm ĐKXĐ: \(x \ne – 1;x \ne 2\) – Quy đồng khử mẫu đúng: 2(x-2) – (x+1) = 3x-11 |
0.25×2 |
|||||||||||||||||||||
|
Bài 2( 1 điểm) |
\(\frac{{3(x – 1)}}{4} + 1 \le \frac{{x + 2}}{3} \Leftrightarrow \frac{{9(x – 1) + 12}}{{4.3}} \le \frac{{4(x + 2)}}{{3.4}}\) a. \( \Leftrightarrow 9x – 9 + 12 \le 4x + 8\) \( \Leftrightarrow 5x \le 5 \Leftrightarrow x \le 1\) Vậy tập nghiệm của phương trình là:\[{\rm{\{ }}x/x \le 1\} \] |
0.25×2 |
||||||||||||||||||||
|
b. Để A dương thì \(\frac{{x – 5}}{{x – 8}} > 0 \Leftrightarrow \left\{ \begin{array}{l}x – 5 < 0\\x – 8 < 0\end{array} \right.(1)\)hoặc \(\left\{ \begin{array}{l}x – 5 > 0\\x – 8 > 0\end{array} \right.(2)\) Giải (1): \(\left\{ \begin{array}{l}x – 5 < 0\\x – 8 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 5\\x < 8\end{array} \right. \Leftrightarrow x < 5\) Giải (2):\(\left\{ \begin{array}{l}x – 5 > 0\\x – 8 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 5\\x > 8\end{array} \right. \Leftrightarrow x > 8\) Vậy x < 5 hoặc x > 8 thì A dương. |
0.25×2 |
|||||||||||||||||||||
|
Bài 3 (1 đ) |
– Chọn ẩn và ĐK đúng: Gọi x là mẫu của phân số phải tìm (ĐK: x∈Z, x≠ 0) – Biểu diễn các ĐL qua ẩn, lập PT đúng:\(\frac{{10 – x}}{{x + 2}} = \frac{1}{5}\) – Giải PT đúng: x = 8 – Trả lời |
0.25
0.25
0.25 0.25 |
||||||||||||||||||||
|
Bài 4 (3 đ) |
a.Tính AD, DC – Tính BC = 10 cm – Lập tỉ số \(\frac{{AD}}{{DC}} = \frac{{AB}}{{BC}} \Rightarrow \frac{{AD}}{{DC + AD}} = \frac{{AB}}{{BC + AB}}\) Thay số, tính: AD = 3cm, DC = 5cm
|
0.5
0.5
0.25 |
||||||||||||||||||||
|
b. – Chứng minh – Vậy \(\Delta AID\)cân – Lập tỉ số \(\frac{{IH}}{{IA}} = \frac{{HB}}{{AB}}\) |
0.25
0.5 |
|||||||||||||||||||||
|
– Chứng minh – Suy ra: \(\frac{{IH}}{{IA}} = \frac{{AD}}{{DC}}\) |
0.5 |
|||||||||||||||||||||
|
2. Diện tích toàn phần của hình hộp chữ nhật là: 2.(3+4).5 + 2.4.3 = 94cm2 |
0.5 |
|||||||||||||||||||||
|
Bài 5 (1 đ) |
a. Với a, b>0, Xét hiệu \(\frac{1}{a} + \frac{1}{b} – \frac{4}{{a + b}} = \frac{{b(a + b) + a(a + b) – 4ab}}{{ab(a + b)}}\) \( = \frac{{{a^2} + {b^2} – 2ab}}{{ab(a + b)}} = \frac{{{{(a – b)}^2}}}{{ab(a + b)}} \ge 0\) Dấu = xảy ra khi a = b. Vậy: \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}\) |
0.5 |
Xem thêm