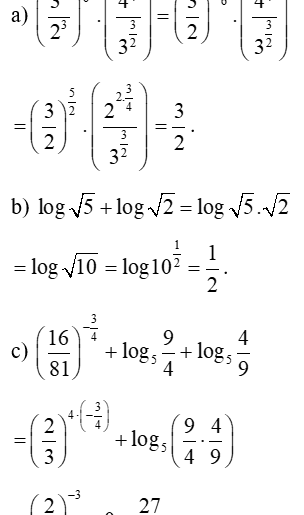Sách bài tập Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 6 trang 24

Giải SBT Toán 11 Bài tập cuối chương 6 trang 24

A. TRẮC NGHIỆM

Giải SBT Toán 11 trang 24

Câu 1 trang 24 SBT Toán 11 Tập 2: Biết rằng 2^a = 9. Tính giá trị của các biểu thức ${\left(\frac{1}{8}\right)}^{\frac{a}{6}}$.

A. $\frac{1}{2}$.

B. $\frac{1}{3}$.

C. $\frac{1}{9}$.

D. 3.

Lời giải:

Đáp án đúng là: B

Ta có: 2^a = 9 ⇒ a = log₂ 9 = 2log₂ 3.

Thay a = 2log₂ 3 vào biểu thức, ta có: ${\left(\frac{1}{8}\right)}^{\frac{2{\log }_{2}3}{6}}=\frac{1}{3}$.

Câu 2 trang 24 SBT Toán 11 Tập 2: Giá trị của biểu thức 2 log₅ 10 + log₅ 0,25 bằng

A. 0.

B. 1.

C. 2

D. 4.

Lời giải:

Đáp án đúng là: C

Ta có: 2 log₅ 10 + log₅ 0,25

= log₅ 10² + log₅ 0,25

= log₅ (100.0,25)

= log₅ 25 = 2.

Câu 3 trang 24 SBT Toán 11 Tập 2: Cho x, y là số dương. Khẳng định nào sau đây là đúng?

A. 2^{log x + log y} = 2^{log x} + 2^{log y}

B. 2^{log (x + y)} = 2^{log x} . 2^{log y}

C. 2^{log (xy)} = 2^{log x} . 2^{log y}

D. 2^{log x . log y} = 2^{log x} + 2^{log y}.

Lời giải:

Đáp án đúng là: C

• 2^{log x + log y} = 2^{log x} . 2^{log y} nên đáp án A sai

• 2^{log x} . 2^{log y} = 2^{log x + log y} nên đáp án B sai

• 2^{log x .log y} = 2^{log x} . 2^{log y} nên đáp án D sai

• 2^{log (xy)} = 2^{log x + log y} = 2^{log x} . 2^{log y} nên đáp án C đúng.

Câu 4 trang 24 SBT Toán 11 Tập 2: Biết rằng x = log₃ 6 + log₉ 4. Giá trị của biểu thức 3^x bằng

A. 6.

B. 12.

C. 24.

D. 48.

Lời giải:

Đáp án đúng là: B

Ta có x = log₃ 6 + log₉ 4 = ${\log }_{3}6+{\log }_{3^2}{2}^2$

= log₃ 6 + log₃ 2 = log₃ (6.2) = log₃ 12.

Thay vào biểu thức, ta có $3^x=3^{{\log }_{3}12}$ = 12.

Câu 5 trang 24 SBT Toán 11 Tập 2: Giá trị của biểu thức (log₂ 25)(log₅ 8) bằng

A. 4.

B. $\frac{1}{4}$.

C. 6.

D. $\frac{1}{6}$.

Lời giải:

Đáp án đúng là: C

Ta có (log₂ 25).(log₅ 8) = (log­₂ 5²).(log₅ 2³)

= 2.log₂ 5 . 3log₅ 2 = 6log₂ 5 . log₅ 2 = 6.

Câu 6 trang 24 SBT Toán 11 Tập 2: Đặt log 3 = a, log 5 = b. Khi đó log₁₅ 50 bằng

A. $\frac{1+2b}{a+b}$.

B. $\frac{a-b}{a+b}$.

C. $\frac{1-b}{a+b}$.

D. $\frac{1+b}{a+b}$.

Lời giải:

Đáp án đúng là: D

Ta có $lo{g}_{15 }50=\frac{\log 50}{\log 15}=\frac{\log \left(5.10\right)}{\log \left(3.5\right)}$

= $\frac{\log 5 +\log 10}{\log 3 +\log 5}=\frac{b+1}{a+b}$.

Câu 7 trang 24 SBT Toán 11 Tập 2: Cho ba số a = 4^0,9 , b = 8^0,5, c = ${\left(\frac{1}{2}\right)}^{-1,6}$. Khẳng định nào sau đây đúng?

A. c > a > b.

B. c > b > a.

C. a > b > c.

D. a > c > b.

Lời giải:

Đáp án đúng là: D

a = 4^0,9 =2^1.8 , b = 8^0,5 = 2^1.5, c = ${\left(\frac{1}{2}\right)}^{-1,6}$ = 2^1,6

Suy ra 2^1,8 > 2^1,5 > 2^1,6 (do cơ số 2 >1 và 1,8 > 1,6 > 1,5).

Do đó $4^{0,9}>{\left(\frac{1}{2}\right)}^{-1,6}>8^{0,5}$.

Câu 8 trang 24 SBT Toán 11 Tập 2: Cho ba số $a=-{\log }_{\frac{1}{3}}\frac{1}{2},b={\log }_{\frac{1}{3}}\frac{1}{2},$ $c=\frac{1}{2}{\log }_{3}5$. Khẳng định nào sau đây đúng?

A. a < b < c.

B. b < a < c.

C. c < a < b.

D. a < c < b.

Lời giải:

Đáp án đúng là: A

Ta có: $a=-{\log }_{\frac{1}{3}}\frac{1}{2}=-{\log }_{3^{-1}}{2}^{-1}=-{\log }_{3}2$;

$b={\log }_{\frac{1}{3}}\frac{1}{2}={\log }_{3^{-1}}{2}^{-1}={\log }_{3}2$;

$c=\frac{1}{2}{\log }_{3}5={\log }_3\sqrt{5}$;

Hàm số log₃ x có cơ số là 3 > 1 nên hàm số đồng biến trên (0; +∞) và $2<\sqrt{5}$ nên $-{\log }_{3}2<{\log }_{3}2<{\log }_3\sqrt{5}$ hay a < b < c

Câu 9 trang 24 SBT Toán 11 Tập 2: Cho 0 < a < 1, x = ${\log }_a\sqrt{2}+{\log }_a\sqrt{3}$, y = $\frac{1}{2}{\log }_{a}5$, z = ${\log }_a\sqrt{14}-{\log }_a\sqrt{2}$. Khẳng định nào sau đây đúng?

A. x < y < z.

B. y < x < z.

C. z < x < y.

D. z < y < x.

Lời giải:

Đáp án đúng là: C

• x = ${\log }_a\sqrt{2}+{\log }_a\sqrt{3}={\log }_a\sqrt{6}$;

• y = ${\log }_4\sqrt{5}$; z = ${\log }_a\sqrt{\frac{14}{2}}={\log }_a\sqrt{7}$.

Ta thấy ${\log }_a\sqrt{7}<lo{g}_a\sqrt{6}<{\log }_a\sqrt{6}$ (do 0 < a< 1).

Do đó z < x < y.

Giải SBT Toán 11 trang 25

Câu 10 trang 25 SBT Toán 11 Tập 2: Cho ba số $a={\log }_{\frac{1}{2}}3, b={\left(\frac{1}{2}\right)}^{0,3},c=2^{\frac{1}{3}}$. Khẳng định nào sau đây đúng?

A. a < b < c.

B. a < c < b.

C. c < a < b.

D. b < a < c.

Lời giải:

$a={\log }_{\frac{1}{2}}3, b={\left(\frac{1}{2}\right)}^{0,3},c=2^{\frac{1}{3}}a={\log }_{\frac{1}{2}}3,\text{\hspace{0.33em}}b={\left(\frac{1}{2}\right)}^{0,3},c=2^{\frac{1}{3}}$

Câu 11 trang 25 SBT Toán 11 Tập 2: Giải phương trình $3^{4x}=\frac{1}{3\sqrt{3}}$

A. $-\frac{1}{4}$.

B. $-\frac{3}{8}$.

C. $\frac{3}{8}$.

D. $\frac{1}{12\sqrt{3}}$.

Lời giải:

Đáp án đúng là: B

Ta có: $4x={\log }_3\frac{1}{3\sqrt{3}}=-{\log }_3\sqrt{27}=-{\log }_3\sqrt{3^3}$

$\iff 4x={\log }_3\frac{1}{3\sqrt{3}}\iff 4x=-{\log }_3\sqrt{27}=-{\log }_3\sqrt{3^3}$

$\iff 4x=-\frac{3}{2}{\log }_{3}3$

$\iff x=-\frac{3}{2}\cdot \frac{1}{4}{\log }_{3}3=\frac{-3}{8}$

$\iff x=\frac{-3}{8}$

Vậy phương trình đã cho có nghiệm x = $\frac{-3}{8}$.

Câu 12 trang 25 SBT Toán 11 Tập 2: Tập nghiệm của bất phương trình 0,3^{3x – 1} > 0,09 là

A. (1; +∞)

B. (-∞; 1).

C. $\left(-\infty ;-\frac{1}{3}\right)$.

D. (0; 1).

Lời giải:

Đáp án đúng là: B

Hàm số 0,3^{3x – 1} và 0,09 = 0,3² có cơ số là 0 < 0,3 < 1 nên hàm số nghịch biến trên ℝ.

Ta có: 0,3^{3x – 1} > 0,09 ⇒ 0,3^{3x – 1} > 0,3²

Do đó, ta có 3x – 1 < 2 ⇒ x < 1 (vì 0 < 0,3 < 1).

Tập nghiệm của S = (−∞; 1).

Câu 13 trang 25 SBT Toán 11 Tập 2: Biết rằng log₃ 4 . log₄ 8 . log₈ x = log₈ 64. Giá trị của x là

A. $\frac{9}{2}$.

B. 9.

C. 27.

D. 81.

Lời giải:

Đáp án đúng là: B

Ta có: log₃ 4 . log₄ 8 . log₈ x = log₈ 64

$\iff {\log }_3{2}^2.lo{g}_2{2}^3.{\log }_{2^3}x={\log }_8{8}^2$

$\iff 2{\log }_{3}2.3.\frac{1}{2}lo{g}_{2}2.\frac{1}{3}{\log }_{2^3}x={\log }_8{8}^2$

⇔ log₃ 2 . log₂ x = 2

⇔ log₃ x = 2 ⇔ x = 3² = 9

Vậy giá trị của x = 9.

Câu 14 trang 25 SBT Toán 11 Tập 2: Giải phương trình log₅ (4x + 5) = 2 + log₅ (x – 4)

A. 9.

B. 15.

C. 4.

D. 5.

Lời giải:

Hướng dẫn giải:

Đáp án đúng là: D

Điều kiện xác định $\left\{\begin{array}{l}4x+5>0\\ x-4>0\end{array}\right.\Rightarrow \left\{\begin{array}{l}x>-\frac{5}{4}\\ x>4\end{array}\right.\Rightarrow x>4$

Ta có: log₅ (4x + 5) = 2 + log₅ (x – 4)

⇔ log₅ (4x + 5) = log₅ 25 + log₅ (x – 4))

⇔ log₅ (4x + 5) = log₅ (25(x – 4))

⇔ 4x + 5 = 25x – 100

⇔ 21x = 105

⇔ x = 5 (nhận)

Vậy nghiệm của phương trình là x = 5.

Câu 15 trang 25 SBT Toán 11 Tập 2: Giả sử α và β là hai nghiệm của phương trình ${\log }_{2}x.lo{g}_{2}3x=-\frac{1}{3}$. Khi đó tích αβ bằng

A. $\frac{1}{3}$.

B. 3.

C. $\sqrt{3}$.

D. log₂ 3.

Lời giải:

Đáp án đúng là: A

Ta có: ${\log }_{2}x.(lo{g}_{2}3+{\log }_{2}x)=-\frac{1}{3}$

Đặt t = log₂ x (x > 0), ta có:

$t({\log }_{2}3+t)=-\frac{1}{3}$

$\iff t^2+t.{\log }_{2}3-\frac{1}{3}=0$

$\iff \left[\begin{array}{l}{t}_1=-1,3353\\ t_2=-0,24962\end{array}\right.\iff \left[\begin{array}{l}{x}_1=\alpha =2^{-1,3353}\\ x_2=\beta =2^{-0,24962}\end{array}\right.$

Vậy tích $\alpha \beta =\frac{1}{3}$.

B. TỰ LUẬN

Bài 1 trang 25 SBT Toán 11 Tập 2: Tính giá trị của các biểu thức

a) ${\left(\frac{27}{8}\right)}^{\frac{5}{6}}.{\left(\frac{4^{\frac{3}{2}}}{3^3}\right)}^{\frac{1}{2}}$;

b) $\log \sqrt{5}+\log \sqrt{2}$;

c) ${\left(\frac{16}{81}\right)}^{-\frac{3}{4}}+{\log }_5\frac{9}{4}+{\log }_5\frac{4}{9}$;

d) ${\log }_{2}7.{\log }_{3}16.{\log }_{9}3.{\log }_{7}9$.

Lời giải:

d) ${\log }_{2}7.{\log }_{3}16.{\log }_{9}3.{\log }_{7}9$

= ${\log }_{2}7.{\log }_3{2}^4.{\log }_{3^2}3.{\log }_7{3}^2$

= $4.{\log }_{2}7.{\log }_{7}3.{\log }_{3}2$ = 4

Bài 2 trang 25 SBT Toán 11 Tập 2: Biết rằng x log₅ 4 = 1. Tìm giá trị của biểu thức 4^x + 4^–x

Lời giải:

Ta có x log₅ 4 = 1 => $x=\frac{1}{{\log }_{5}4}={\log }_{4}5$.

Khi đó 4^x + 4^–x = 4^log₄ ⁵ + 4^–log₄ ⁵ = 5 + 5^–1 = $\frac{26}{5}$.

Vậy giá trị của biểu thức đã cho là $\frac{26}{5}$.

Bài 3 trang 25 SBT Toán 11 Tập 2: Biết rằng a = 10^x, b = 10^x. Hãy biểu thị biểu thức A = ${\log }_{a^2}\sqrt[3]{b}$ theo x và y

Lời giải:

A = ${\log }_{a^2}\sqrt[3]{b}={\log }_{{10}^{2x}}{10}^{\frac{y}{3}}$

= $\frac{1}{2x}.\frac{y}{3}{\log }_{10}10=\frac{y}{6x}$

Bài 4 trang 25 SBT Toán 11 Tập 2: Giải các phương trình sau:

a) $4^x=\sqrt{2\sqrt{2}}$;

b) 9^5x = 27^{x – 2};

c) ${\log }_{81}x=\frac{1}{2}$;

d) ${\log }_{\frac{1}{2}}(3x+1)={\log }_{\frac{1}{2}}(4x-1)$;

e) ${\log }_5(x-2)+{\log }_5(x+2)=1$;

g) ${\log }_{x}8=\frac{3}{4}$.

Lời giải:

a) $4^x=\sqrt{2\sqrt{2}}={\left(\sqrt{8}\right)}^{\frac{1}{2}}={\left(8^{\frac{1}{2}}\right)}^{\frac{1}{2}}={\left(8\right)}^{\frac{1}{2}\cdot \frac{1}{2}}=8^{\frac{1}{4}}$

Khi đó $4^x=8^{\frac{1}{4}}\Rightarrow x={\log }_4{8}^{\frac{1}{4}}=\frac{1}{4}{\log }_{4}8=\frac{3}{8}$.

Vậy phương trình có nghiệm là x = $\frac{3}{8}$.

b) 9^5x = 27^{x – 2} ⇒ 3^10x = 3^{3(x – 2)};

10x = 3(x – 2) => 7x = – 6 => x = $-\frac{6}{7}$.

Vậy phương trình có nghiệm là x = $-\frac{6}{7}$.

c) Điều kiện x > 0

Ta có ${\log }_{81}x=\frac{1}{2}\Rightarrow x={81}^{\frac{1}{2}}=\sqrt{81}=9$.

Vậy phương trình có nghiệm là x = 9.

d) Điều kiện xác định $\left\{\begin{array}{l}3x+1>0\\ 4x-1>0\end{array}\right.\Rightarrow \left\{\begin{array}{l}x>-\frac{1}{3}\\ x>\frac{1}{4}\end{array}\right.\Rightarrow x>\frac{1}{4}$.

Khi đó, phương trình đã cho tương đương với

${\log }_{\frac{1}{2}}(3x+1)={\log }_{\frac{1}{2}}(4x-1)$

⇔ 3x + 1 = 4x – 1

⇔ x = 2 (nhận)

Vậy phương trình có nghiệm là x = 2.

e) ${\log }_5(x-2)+{\log }_5(x+2)=1$

Điều kiện xác định $\left\{\begin{array}{l}x-2>0\\ x+2>0\end{array}\right.\Rightarrow \left\{\begin{array}{l}x>2\\ x>-2\end{array}\right.\Rightarrow x>2$

Khi đó, phương trình đã cho tương đương với

${\log }_5(x-2)+{\log }_5(x+2)=1$

$\iff {\log }_5(x+2)(x-2)=1$

$\iff {\log }_5(x^2-4)=1$

⇔ x² – 4 = 5 ⇔ x² = 9

$\iff x=\sqrt{9}=3$ (nhận) hoặc $x=-\sqrt{9}=-3$ (loại)

Vậy phương trình có nghiệm là x = 3.

g) ${\log }_{x}8=\frac{3}{4}$

$\iff {\log }_x{2}^3=\frac{3}{4}$

$\iff 3{\log }_{x}2=\frac{3}{4}$

$\iff {\log }_{x}2=\frac{1}{4}$

$\iff 2=x^{\frac{1}{4}}$

$\iff 2^4={\left(x^{\frac{1}{4}}\right)}^4\iff x=16$

Vậy nghiệm của phương trình là x = 16.

Bài 5 trang 25 SBT Toán 11 Tập 2: Giải các bất phương trình sau:

a) 32^2x ≥ 64^{x – 2} ;

b) $25.{\left(\frac{2}{5}\right)}^{x^2+2x+2}>4$;

c) log (11x + 1) < 2;

d) ${\log }_{\frac{1}{3}}(3x-1)\ge {\log }_{\frac{1}{3}}(2x+1)$.

Lời giải:

a) 32^2x ≥ 64^{x – 2}

⇔ 2^10x ≥ 2^{6(x – 2)}

⇔ 10x ≥ 6(x – 2) (do 2 > 1)

⇔ 4x ≥ – 12 ⇔ x ≥ – 3.

Vậy tập nghiệm của bất phương trình đã cho là S = (−3; +∞).

b) $25.{\left(\frac{2}{5}\right)}^{x^2+2x+2}>4$

$\iff {\left(\frac{2}{5}\right)}^{x^2+2x+2}>\frac{4}{25}$

$\iff {\left(\frac{2}{5}\right)}^{x^2+2x+2}>{\left(\frac{2}{5}\right)}^2$

⇔ x² + 2x + 2 < 2 (do $0<\frac{2}{5}<1$).

⇔ x² + 2x < 0

⇔ – 2 < x < 0.

Vậy tập nghiệm của bất phương trình là S = (–2; 0).

c) log (11x + 1) < 2

Điều kiện: 11x +1 > 0 $\iff x>-\frac{1}{11}$.

Khi đó, ta có: log (11x + 1) < 2 ⇔ 11x + 1 < 10²

⇔ 11x < 99 $\iff x<\frac{99}{11}=9$.

Kết hợp điều kiện, ta có nghiệm của bất phương trình là S = $\left(-\frac{1}{11}; 9\right)$.

d) ${\log }_{\frac{1}{3}}\left(3x-1\right)\ge {\log }_{\frac{1}{3}}\left(2x+1\right)$

Điều kiện: $\left\{\begin{array}{l}3x-1>0\\ 2x+1>0\end{array}\right.\Rightarrow \left\{\begin{array}{l}x>\frac{1}{3}\\ x>-\frac{1}{3}\end{array}\right.\Rightarrow x>\frac{1}{3}$

Khi đó, ta có ${\log }_{\frac{1}{3}}\left(3x-1\right)\ge {\log }_{\frac{1}{3}}\left(2x+1\right)$

⇔ 3x – 1 ≤ 2x + 1

⇔ x ≤ 2 (do $0<\frac{1}{3}<1$)

Kết hợp điều kiện, ta có nghiệm của bất phương trình là S = $\left(-\frac{1}{3}; 2\right]$.

Bài 6 trang 25 SBT Toán 11 Tập 2: Tính giá trị của biểu thức

A = $\log \left(1+\frac{1}{1}\right)+log\left(1+\frac{1}{2}\right)+log\left(1+\frac{1}{3}\right)+...+log\left(1+\frac{1}{99}\right)$.

Lời giải:

A = $\log \left(1+\frac{1}{1}\right)+log\left(1+\frac{1}{2}\right)+log\left(1+\frac{1}{3}\right)+...+log\left(1+\frac{1}{99}\right)$

= $\log 2+\log \frac{3}{2}+\log \frac{4}{3}+....+\log \frac{100}{9}$

= $\log \left(2\cdot \frac{3}{2}\cdot \frac{4}{3}\cdot ....\cdot \frac{100}{9}\right)=\log 100=2$.

Bài 7 trang 25 SBT Toán 11 Tập 2: Cho α là số thỏa mãn 3^α – 3^–α = 2. Tìm giá trị của các biểu thức:

a) 3^α + 3^–α ;

b) 9^α – 9^–α.

Lời giải:

a) ${\left(3^{\alpha }+3^{-\alpha }\right)}^2=3^{2\alpha }+2+3^{-2\alpha }$

= ${\left(3^{\alpha }-3^{-\alpha }\right)}^2+4$ = 2² + 4 = 8

=> $3^{\alpha }+3^{-\alpha }=2\sqrt{2}$ (do $3^{\alpha }+3^{-\alpha }$ > 0).

b) $9^{\alpha }-9^{-\alpha }=\left(3^{\alpha }+3^{-\alpha }\right)\left(3^{\alpha }-3^{-\alpha }\right)$

= $=2\sqrt{2}.2=4\sqrt{2}$.

Bài 8 trang 25 SBT Toán 11 Tập 2: Công thức M = $M_0{\left(\frac{1}{2}\right)}^{\frac{t}{T}}$ cho biết khối lượng của một chất phóng xạ sau thời gian t kể từ thời điểm nào đó (gọi là thời điểm ban đầu), M₀là khối lượng ban đầu, T là chu kì bán rã của chấy phóng xạ đó (cứ sau mỗi chu kì, khối lượng của chất phóng xạ giảm đi một nửa). Trong một phòng thí nghiệm, với khối lượng 200 g radon ban đầu, sau 16 ngày, chỉ còn lại 11 g. Chu kì bán rã của radon bằng bao nhiêu?

Lời giải:

a) Áp dụng công thức: 11 = $200{\left(\frac{1}{2}\right)}^{\frac{16}{T}}$

$\iff \frac{16}{T}={\log }_{\frac{1}{2}}\frac{11}{200}=lo{g}_2\frac{200}{11}$

$\iff T=\frac{16}{lo{g}_2\frac{200}{11}}\approx 3,8$ (ngày).

Vậy chu kì bán rã của radon khoảng 3,8 ngày.

Bài 9 trang 25 SBT Toán 11 Tập 2: Công thức log x = 11,8 + 1,5M cho biết mối liên hệ giữa năng lượng x tạo ra (tính theo erg, 1 erg tương đương 10^–7 jun) với độ lớn M theo thang Richter của một trận động đất.

a) Trận động đất có độ lớn 5 độ Richter tạo ra năng lượng gấp bao nhiêu lần so với trận động đất có độ lớn 3 độ Richter?

b) Người ra ước lượng rằng một trận động đất có độ lớn khoảng từ 4 đến 6 độ Richter. Năng lượng do trận động đất tạo ra nằm trong khoảng nào?

Lời giải:

a) Gọi x_1, x₂ (erg) lần lượt là năng lượng tạo ra của hai trận động đất có độ lớn lần lượt là M₁ = 5, M₂ = 3 (độ Richter).

Ta có: log x₁ = 11,8 + 1,5M₁; log x₂ = 11,8 + 1,5M₂.

=> log x₁ – log x₂ = 1,5 (M₁ – M₂)

=> $\log \frac{x_1}{x_2}=3\Rightarrow \frac{x_1}{x_2}$ = 10³ = 1000.

Như vậy, năng lượng mà trận động đất độ lớn 5 độ Richter gấp 1000 lần so với trận động đất có độ lớn 3 độ Richter.

b) Ước lượng rằng một trận động đất có độ lớn khoảng từ 4 đến 6 độ Richter, ta có:

11,8 + 1,5 . 4 ≤ log x ≤ 11,8 + 1,5 . 6

=> 17,8 ≤ log x ≤ 20,8

=> 10^17,8 ≤ x ≤ 10^20,8

Như vậy, nặng lượng do trận động đất tạo ra nằm trong khoảng 10^17,8 ≤ x ≤ 10^20,8.

Xem thêm các bài giải SBT Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài tập cuối chương 6

Bài 1: Đạo hàm

Bài 2: Các quy tắc tính đạo hàm

Bài tập cuối chương 7

Bài 1: Hai đường thẳng vuông góc