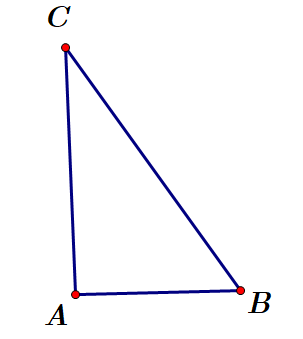
Trong không gian cho tam giác\(ABC\) vuông tại \(A\),\(AB = a\) và \(\widehat {ACB} = {30^o}\). Tính thể tích \(V\) của khối nón nhận được khi quay tam giác \(ABC\) quanh cạnh \(AC\).
A. \(V = \pi {a^3}\).
B. \(V = \sqrt 3 \pi {a^3}\).
C.\(V = \frac{{\sqrt 3 \pi {a^3}}}{9}\) .
D. \(V = \frac{{\sqrt 3 \pi {a^3}}}{3}\).
Lời giải:
Ta có \(AC = AB.\cot {30^o} = a\sqrt 3 \). Vậy thể tích khối nón là: \(V = \frac{1}{3}\pi {a^2}.a\sqrt 3 = \frac{{\pi {a^3}\sqrt 3 }}{3}\).
===========
Tương tự Câu 45 BÀI TOÁN THỰC TẾ KHỐI TRÒN XOAY – VẬN DỤNG CAO – PHÁT TRIỂN Toán TK 2024