Câu hỏi:
Cho hàm số (y=fleft( x right)). Đồ thị hàm số (y=f’left( x right)) như hình bên. Tìm số điểm cực trị của hàm số (gleft( x right)=fleft( {{x}^{2}}-3 right).)
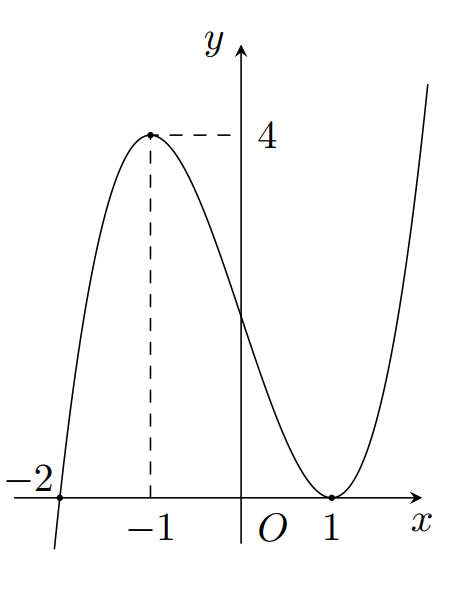
Lời giải tham khảo:
Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới.
Đề thi thử TN THPT QG năm 2021 môn TOÁN
Đáp án đúng: B
(g’left( x right) = 2xf’left( {{x^2} – 3} right))
(g’left( x right) = 0 Leftrightarrow left[ begin{array}{l}
x = 0\
f’left( {{x^2} – 3} right) = 0
end{array} right. Leftrightarrow left[ begin{array}{l}
x = 0\
{x^2} – 3 = – 2\
{x^2} – 3 = 1left( {nghiem{rm{ }}kep} right)
end{array} right. Leftrightarrow left[ begin{array}{l}
x = 0\
x = pm 1\
x = pm 2left( {nghiem{rm{ }}kep} right)
end{array} right.)
Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.
