Cho hàm số (fleft( x right)) có bảng xét dấu đạo hàm như sau:
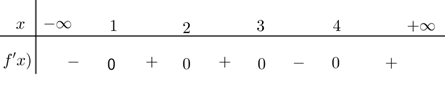
Hàm số (y = fleft( {3x + 1} right) – {x^3} + 3x) đồng biến trên khoảng nào dưới đây?
A. (left( { – 1,;, – frac{1}{3}} right)). B. (left( {frac{1}{4},;,frac{1}{3}} right)). C. (left( {frac{2}{3},;,1} right)). D. (left( {frac{3}{4},;1} right))
Lời giải
Ta có (y’ = 3f’left( {3x + 1} right) – 3{x^2} + 3)
Để hàm số đồng biến trên khoảng (K) ta cần có (y’ = 3f’left( {3x + 1} right) – 3{x^2} + 3 ge 0,), (forall x in K)
( Leftrightarrow f’left( {3x + 1} right) + left( { – {x^2} + 1} right) ge 0,,,forall x in K) ta chỉ cần chọn (x) thỏa mãn (left{ begin{array}{l}f’left( {3x + 1} right) ge 0\ – {x^2} + 1 ge 0end{array} right.)
( Leftrightarrow left{ begin{array}{l}left[ begin{array}{l}1 le 3x + 1 le 3\3x + 1 ge 4end{array} right.\ – 1 le x le 1end{array} right.)( Leftrightarrow left{ begin{array}{l}left[ begin{array}{l}0 le x le frac{2}{3}\x ge 1end{array} right.\ – 1 le x le 1end{array} right.)( Rightarrow 0 le x le frac{2}{3}), ta thấy (left( {frac{1}{4},;,frac{1}{3}} right) subset left[ {0,;,frac{2}{3}} right]).
