adsense
Giải bài tập Bài 2 Hệ bất phương trình bậc nhất hai ẩn (Cánh diều)
========
Giải câu 1 bài hệ bất phương trình bậc nhất hai ẩn
Đề bài:
Bài tập 1. Kiểm tra xem mỗi cặp số $(x ; y)$ đã cho có là nghiệm của hệ bất phương trình tương ứng không.
a. $left{begin{array}{l}3 x+2 y geq-6 \ x+4 y>4end{array} quad (0 ; 2),(1 ; 0) ;right.$
b. $left{begin{array}{c}4 x+y leq-3 \ -3 x+5 y geq-12end{array} quad(-1 ;-3),(0 ;-3) .right.$
Bài giải:
a. $left{begin{array}{l}3 x+2 y geq-6 \ x+4 y>4end{array} quad (0; 2),(1; 0)right.$
- Thay $x=0;y=2$ vào 2 bất phương trình của hệ, ta có:
$3.0+2.2=4geq-6$ là mệnh đề đúng; $0+4.2=8>4$ là mệnh đề đúng.
Vậy $(0;2)$ là nghiệm chung của 2 bất phương trình nên $(0;2)$ là nghiệm của hệ bất phương trình.
- Thay $x=1;y=0$ vào 2 bất phương trình của hệ, ta có:
$3.1+2.0=3geq-6$ là mệnh đề đúng; $1+4.0=1>4$ là mệnh đề sai.
Vậy $(1;0)$ không là nghiệm chung của 2 bất phương trình nên $(1;0)$ không là nghiệm của hệ bất phương trình.
b. $left{begin{array}{c}4 x+y leq-3 \ -3 x+5 y geq-12end{array} quad(-1 ;-3),(0 ;-3)right.$
- Thay $x=-1;y=-3$ vào 2 bất phương trình của hệ, ta có:
$4.(-1)+(-3)=-7 leq-3$ là mệnh đề đúng; $-3.(-1)+5.(-3)=-12 geq-12$ là mệnh đề đúng.
Vậy $(-1;-3)$ là nghiệm chung của 2 bất phương trình nên $(-1;-3)$ là nghiệm của hệ bất phương trình.
- Thay $x=0;y=-3$ vào 2 bất phương trình của hệ, ta có:
$4.0+(-3)=-3 leq-3$ là mệnh đề đúng; $-3.0+5.(-3)=-15 geq-12$ là mệnh đề sai
Vậy $(0;-3)$ không là nghiệm chung của 2 bất phương trình nên $(0;-3)$ không là nghiệm của hệ bất phương trình.
Giải câu 2 bài hệ bất phương trình bậc nhất hai ẩn
Đề bài:
Bài tập 2. Biểu diễn miền nghiệm của hệ bất phương trình:
a. $left{begin{array}{c}x+2 y<-4 \ y geq x+5end{array}right.$
b. $left{begin{array}{r}4 x-2 y>8 \ x geq 0 \ y leq 0end{array}right.$
Bài giải:
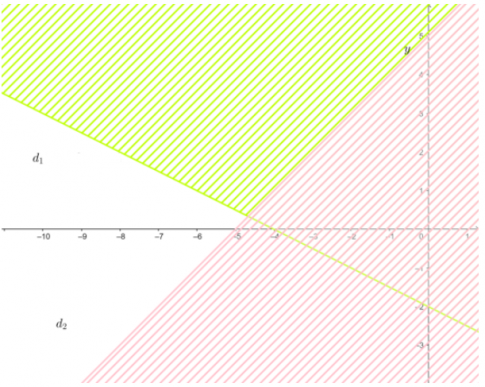
a. $left{begin{array}{c}x+2 y<-4 \ y geq x+5 end{array}right.$
- Trong cùng mặt phẳng tọa độ $Oxy$, vẽ hai đường thẳng: $d_{1}:x+2 y=-4$; $d_{2}:y = x+5$.
Do tọa độ điểm $O(0;0)$ không thỏa mãn các bất phương trình trong hệ nên miền nghiệm của từng bất phương trình trong hệ lần lượt là những nửa mặt phẳng không bị gạch không chứa điểm $O(0;0)$.
adsense
- Phần không bị gạch (không chứa điểm $O(0;0)$ là miền nghiệm của hệ bất phương trình đã cho.
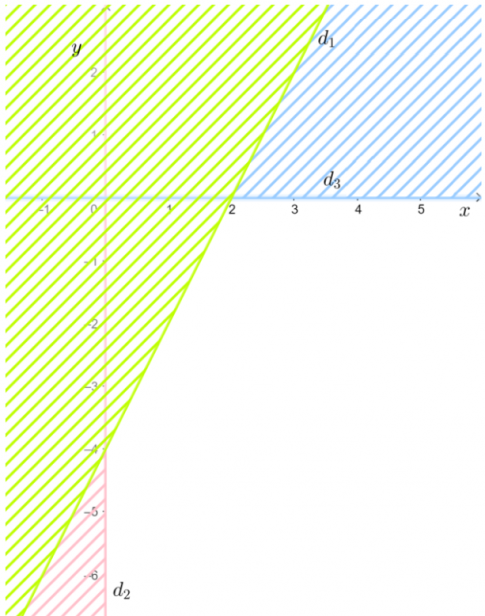
b. $left{begin{array}{r}4 x-2 y>8 (1)\ x geq 0 (2)\ y leq 0 (3)end{array}right.$
- Trong cùng mặt phẳng tọa độ $Oxy$, vẽ ba đường thẳng: $d_{1}:4 x-2 y=8$; $d_{2}:x=0$; $d_{3}:y=0$.
- Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình. Miền nghiệm của hệ bất phương trình là phần không bị gạch (không chứa điểm $O(0;0)$) do tọa độ điểm $O(0;0)$ không thỏa mãn bất phương trình (1); thỏa mãn bất phương trình (2), (3) trong hệ.
Giải câu 3 bài hệ bất phương trình bậc nhất hai ẩn
Đề bài:
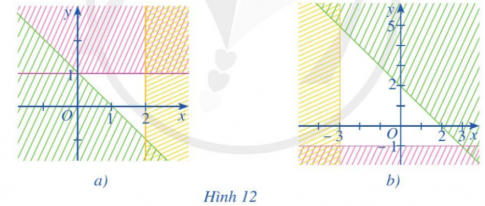
Bài tập 3. Miền không bị gạch ở mỗi Hình $12a, 12b$ là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
a. $left{begin{aligned} x+y & leq 2 \ x & geq-3 \ y & geq-1 end{aligned}right.$
b. $left{begin{array}{l}y leq x \ x leq 0 \ y geq-3end{array}right.$
c. $left{begin{array}{l}y geq-x+1 \ x leq 2 \ y leq 1end{array}right.$
Bài giải:
- Hình 12a: Hệ bất phương trình c vì có 3 đường thẳng là: $x=2$; $y=1$ và $x+y=1$
- Hình 12b: Hệ bất phương trình a vì có 3 đường thẳng là: $x=-3$; $y=-1$; $x+y=2$
Giải câu 4 bài hệ bất phương trình bậc nhất hai ẩn
Đề bài:
Bài tập 4. Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc. Phân xưởng làm việc không quá 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.
Bài giải:
Gọi $x,y$ lần lượt là số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất $(x,y∈mathbb{N})$.
Theo giả thiết, $x,y$ thỏa mãn các điều kiện $0leq xleq 200$; $0leq yleq 240$.
Thời gian làm $y$ chiếc kiểu thứ hai là $frac{y}{60}$ (giờ)
Do thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai $Rightarrow$ Thời gian để làm $x$ chiếc mũ kiểu thứ nhất $frac{x}{30}$ (giờ)
Phân xưởng làm việc không quá 8 tiếng mỗi ngày nên ta có: $frac{x}{30} + frac{y}{60} leq 8$ $Leftrightarrow$ $2x+y leq 480$
Tổng số tiền lãi là: $T=24x+15y$
Bài toán đưa về: Tìm $x,y$ là nghiệm của hệ bất phương trình $left{begin{aligned} 0leq xleq 200 \ 0leq yleq 240 \ 2x+y leq 480 end{aligned}right.$ sao cho $T=24x+15y$ có giá trị lớn nhất.
Xác định miền nghiệm của hệ bất phương trình:

Giá trị của biểu thức $T=24x+15y$ đạt giá trị lớn nhất tại cặp số $(x;y)$ là tọa độ của một trong các đỉnh của ngũ giác $ABCDE$.
- $A(0;240) Rightarrow T=3600$
- $B(120;240) Rightarrow T=6480$
- $C(0;0) Rightarrow T=0$
- $D(200;80) Rightarrow T=6000$
- $E(200;0) Rightarrow T=4800$
Vậy để tiền lãi thu được là cao nhất thì phân xưởng cần sản xuất 120 mũ kiểu thứ nhất và 240 mũ kiểu thứ hai trong một ngày.
