adsense
Giải bài tập Cuối chương 4 (Kết nối)
————-
Giải bài 4.27 trang 71 SGK Toán 10 Kết nối tri thức tập 1
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương?
A. (overrightarrow u = (2;3)) và (overrightarrow v = left( {frac{1}{2};6} right))
B. (overrightarrow a = (sqrt 2 ;6)) và (overrightarrow b = (1;3sqrt 2 ))
C. (overrightarrow i = (0;1)) và (overrightarrow j = (1;0))
D. (overrightarrow c = (1;3)) và (overrightarrow d = (2; – 6))
Phương pháp giải
Cho (overrightarrow a = (x;y)) và (overrightarrow b = (z,t)) ((z,t ne 0))
+) Nếu (frac{x}{z} = frac{y}{t} = k) thì (overrightarrow a ) và (overrightarrow b ) cùng phương
+) Nếu (frac{x}{z} ne frac{y}{t}) thì (overrightarrow a ) và (overrightarrow b ) không cùng phương.
Hướng dẫn giải
A. Ta có: (frac{2}{{frac{1}{2}}} = 4 ne frac{3}{6}) nên (overrightarrow u ) và (overrightarrow v ) không cùng phương.
B. Ta có: (frac{{sqrt 2 }}{1} = frac{6}{{3sqrt 2 }} = sqrt 2 > 0) nên (overrightarrow a ) và (overrightarrow b ) cùng phương, hơn nữa là cùng hướng
Chọn đáp án B.
C. Ta có: (overrightarrow i .overrightarrow j = 0.1 + 1.0 = 0 Rightarrow overrightarrow i bot overrightarrow j )
Vậy (overrightarrow i ) và (overrightarrow j ) không cùng phương.
D. Ta có: (frac{1}{2} ne frac{3}{{ – 6}}) nên (overrightarrow c ) và (overrightarrow d ) không cùng phương.
Giải bài 4.28 trang 71 SGK Toán 10 Kết nối tri thức tập 1
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
A. (overrightarrow u = (2;3)) và (overrightarrow v = left( {4;6} right))
B. (overrightarrow a = (1; – 1)) và (overrightarrow b = ( – 1;1))
C. (overrightarrow z = (a;b)) và (overrightarrow t = ( – b;a))
D. (overrightarrow n = (1;1)) và (overrightarrow k = (2;0))
Phương pháp giải
+) Cho (overrightarrow u ;(x;y),;overrightarrow v ;(z;t)) thì (overrightarrow u .overrightarrow v = x.z + y.t)
+) (overrightarrow u; botoverrightarrow vLeftrightarrow overrightarrow u .;overrightarrow v = 0)
Hướng dẫn giải
A. Ta có: (overrightarrow u .overrightarrow v = 2.4 + 3.6 = 26 ne 0) nên (overrightarrow u ) và (overrightarrow v ) không vuông góc với nhau.
B. Ta có: (overrightarrow a .overrightarrow b = 1.( – 1) + ( – 1).1 = – 2 ne 0) nên (overrightarrow a ) và (overrightarrow b ) không vuông góc với nhau.
C. Ta có: (overrightarrow z .overrightarrow t = a.( – b) + b.a = 0) nên (overrightarrow z ) và (overrightarrow t ) vuông góc với nhau.
D. Ta có: (overrightarrow n .overrightarrow k = 1.2 + 1.0 = 2 ne 0) nên (overrightarrow n ) và (overrightarrow k ) không vuông góc với nhau.
Chọn đáp án C
Giải bài 4.29 trang 71 SGK Toán 10 Kết nối tri thức tập 1
Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?
A. (overrightarrow a = (1;1))
B. (overrightarrow b = (1; – 1))
C. (overrightarrow c = left( {2;frac{1}{2}} right))
D. (overrightarrow d = left( {dfrac{1}{{sqrt 2 }};dfrac{{ – 1}}{{sqrt 2 }}} right))
Phương pháp giải
Tính độ dài vectơ (overrightarrow a ;(x;y)) theo công thức: (|overrightarrow a |, = sqrt {{x^2} + {y^2}} ).
Hướng dẫn giải
A. Ta có: (overrightarrow a = (1;1) Rightarrow ;|overrightarrow a |; = sqrt {{1^2} + {1^2}} = sqrt 2 ne 1). (Loại)
B. Ta có: (overrightarrow b = (1; – 1) Rightarrow ;|overrightarrow b |; = sqrt {{1^2} + {{( – 1)}^2}} = sqrt 2 ne 1). (Loại)
C. Ta có: (overrightarrow c = left( {2;dfrac{1}{2}} right) Rightarrow ;|overrightarrow c |; = sqrt {{2^2} + {{left( {dfrac{1}{2}} right)}^2}} = dfrac{{sqrt {17} }}{2} ne 1). (Loại)
D. Ta có: (overrightarrow d = left( {dfrac{1}{{sqrt 2 }};frac{{ – 1}}{{sqrt 2 }}} right) Rightarrow ;|overrightarrow a |; = sqrt {{{left( {frac{1}{{sqrt 2 }}} right)}^2} + {{left( {frac{{11}}{{sqrt 2 }}} right)}^2}} = 1). (Thỏa mãn yc)
Chọn D
Giải bài 4.30 trang 71 SGK Toán 10 Kết nối tri thức tập 1
Góc giữa vectơ (overrightarrow a = left( {1; – 1} right)) và vectơ (overrightarrow b = ( – 2;0)) có số đo bằng:
A. ({90^o})
B. ({0^o})
C. ({135^o})
D. ({45^o})
Phương pháp giải
Tính (overrightarrow a .overrightarrow b ).
+) Nếu (overrightarrow a .overrightarrow b = 0) thì góc giữa 2 vectơ bằng ({90^o}).
+) Nếu (overrightarrow a .overrightarrow b ne 0) thì (cos left( {overrightarrow a ,overrightarrow b } right) = frac{{overrightarrow a .overrightarrow b }}{{|overrightarrow a |.;|overrightarrow b |}})
Hướng dẫn giải
Ta có: (overrightarrow a .overrightarrow b = 1.( – 2) + ( – 1).0 = – 2 ne 0).
Lại có: (|overrightarrow a | = sqrt {{1^2} + {{( – 1)}^2}} = sqrt 2 ;;|overrightarrow b | = sqrt {{{( – 2)}^2} + {0^2}} = 2.)
( Rightarrow cos left( {overrightarrow a ,overrightarrow b } right) = frac{{overrightarrow a .overrightarrow b }}{{|overrightarrow a |.;|overrightarrow b |}} = frac{{ – 2}}{{sqrt 2 .2}} = frac{{ – sqrt 2 }}{2})
( Rightarrow left( {overrightarrow a ,overrightarrow b } right) = {135^o})
Chọn C
Giải bài 4.31 trang 71 SGK Toán 10 Kết nối tri thức tập 1
Khẳng định nào sau đây là đúng?
A. (( {overrightarrow a .overrightarrow b } )overrightarrow c = overrightarrow a ,,( {overrightarrow b .overrightarrow c }))
B. ({( {overrightarrow a .overrightarrow b })^2} = {overrightarrow a ^2},.,{overrightarrow b ^2})
C. (overrightarrow a .overrightarrow b = | {overrightarrow a } |.left| {overrightarrow b } right|,sin ( {overrightarrow a ,overrightarrow b } ))
D. (overrightarrow a ,,( {overrightarrow b – overrightarrow c }) = overrightarrow a .overrightarrow b – overrightarrow a .,overrightarrow c )
Phương pháp giải
(overrightarrow a .overrightarrow b = | {overrightarrow a }|.| {overrightarrow b }|,cos ( {overrightarrow a ,overrightarrow b }))
Hướng dẫn giải
Chọn D. Đây là một tính chất của tích vô hướng.
A. Sai vì (({overrightarrow a .overrightarrow b})overrightarrow c = [ {|overrightarrow a |.|overrightarrow b |;,cos ( {overrightarrow a ,overrightarrow b } )} ].overrightarrow c ne )(overrightarrow a ,,( {overrightarrow b .overrightarrow c }) = overrightarrow a ,,[ {|overrightarrow b |.|overrightarrow c |;,cos ( {overrightarrow b ,overrightarrow c })}])
B. Sai vì ((overrightarrow a .overrightarrow b)^2 = {[{overrightarrow a .overrightarrow b = | {overrightarrow a } |.| {overrightarrow b }|,cos ( {overrightarrow a ,overrightarrow b })}]^2} = {overrightarrow a ^2},.,{overrightarrow b ^2}.{cos ^2}( {overrightarrow a ,overrightarrow b } ))( ne ;;{overrightarrow a ^2},.,{overrightarrow b ^2})
C. Sai vì (overrightarrow a .overrightarrow b = | {overrightarrow a }|.| {overrightarrow b } |,cos ( {overrightarrow a ,overrightarrow b }) ne | {overrightarrow a }|.| {overrightarrow b }|,sin ( {overrightarrow a ,overrightarrow b }))
Giải bài 4.32 trang 71 SGK Toán 10 Kết nối tri thức tập 1
Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?
A. (left( {overrightarrow {AB} ,overrightarrow {BD} } right) = {45^o})
B. (left( {overrightarrow {AC} ,overrightarrow {BC} } right) = {45^o}) và (overrightarrow {AC} .overrightarrow {BC} = {a^2})
C. (overrightarrow {AC} .overrightarrow {BD} = {a^2}sqrt 2 )
D. (overrightarrow {BA} .overrightarrow {BD} = – {a^2})
Phương pháp giải
Tính tích vô hướng bằng công thức: (overrightarrow a .overrightarrow b = left| {overrightarrow a } right|.left| {overrightarrow b } right|,cos left( {overrightarrow a ,overrightarrow b } right)).
Hướng dẫn giải
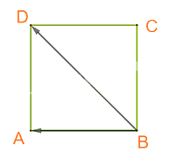
A. Ta có: (left( {overrightarrow {AB} ,overrightarrow {BD} } right) = left( {overrightarrow {BE} ,overrightarrow {BD} } right) = {135^o} ne {45^o}.) Vậy A sai.
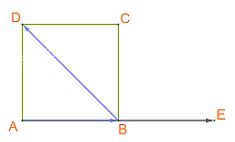
B. Ta có: (left( {overrightarrow {AC} ,overrightarrow {BC} } right) = left( {overrightarrow {CF} ,overrightarrow {CG} } right) = {45^o}) và (overrightarrow {AC} .overrightarrow {BC} = AC.BC.cos {45^o} = asqrt 2 .a.frac{{sqrt 2 }}{2} = {a^2}.)
Vậy B đúng.
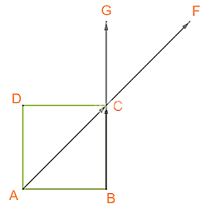
C. Dễ thấy (AC bot BD) nên (overrightarrow {AC} .overrightarrow {BD} = 0 ne {a^2}sqrt 2.) Vậy C sai.
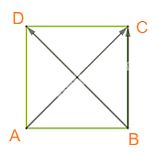
D. Ta có: (left( {overrightarrow {BA} .overrightarrow {BD} } right) = {45^o}) ( Rightarrow overrightarrow {BA} .overrightarrow {BD} = BA.BD.cos {45^o} = a.asqrt 2 .frac{{sqrt 2 }}{2} = {a^2} ne – {a^2}.) Vậy D sai.
Chọn B
Giải bài 4.33 trang 71 SGK Toán 10 Kết nối tri thức tập 1
Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3 MC.
a) Tìm mối liên hệ giữa hai vectơ (overrightarrow {MB} ) và (overrightarrow {MC} )
b) Biểu thị vectơ (overrightarrow {AM} ) theo hai vectơ (overrightarrow {AB} ) và (overrightarrow {AC} ).
Phương pháp giải
+) Nếu (MB = k.MC) và (overrightarrow {MB} ) và (overrightarrow {MC} ) ngược hướng thì (overrightarrow {MB} = -k.overrightarrow {MC})
+) (overrightarrow {AM} = overrightarrow {AB} + overrightarrow {BM} ) (quy tắc cộng)
+) (overrightarrow {BC} = overrightarrow {AC} – overrightarrow {AB} ) (quy tắc hiệu)
Hướng dẫn giải
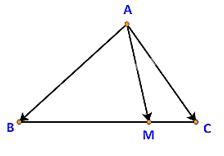
a) M thuộc cạnh BC nên vectơ (overrightarrow {MB} ) và (overrightarrow {MC} ) ngược hướng với nhau.
Lại có: MB = 3 MC ( Rightarrow overrightarrow {MB} = – 3.overrightarrow {MC} )
b) Ta có: (overrightarrow {AM} = overrightarrow {AB} + overrightarrow {BM} )
Mà (BM = dfrac{3}{4}BC) nên (overrightarrow {BM} = dfrac{3}{4}overrightarrow {BC} )
( Rightarrow overrightarrow {AM} = overrightarrow {AB} + dfrac{3}{4}overrightarrow {BC} )
Lại có: (overrightarrow {BC} = overrightarrow {AC} – overrightarrow {AB} ) (quy tắc hiệu)
( Rightarrow overrightarrow {AM} = overrightarrow {AB} + dfrac{3}{4}left( {overrightarrow {AC} – overrightarrow {AB} } right) = dfrac{1}{4}.overrightarrow {AB} + dfrac{3}{4}.overrightarrow {AC} )
Vậy (overrightarrow {AM} = dfrac{1}{4}.overrightarrow {AB} + dfrac{3}{4}.overrightarrow {AC} )
Giải bài 4.34 trang 72 SGK Toán 10 Kết nối tri thức tập 1
Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:
(overrightarrow {MA} + overrightarrow {MC} = overrightarrow {MB} + overrightarrow {MD} ).
Phương pháp giải
ABCD là hình bình hành thì: (overrightarrow {AB} = overrightarrow {DC} )
Hướng dẫn giải
Do ABCD là hình bình hành nên (overrightarrow {AB} = overrightarrow {DC} )
(begin{array}{l} Rightarrow overrightarrow {AM} + overrightarrow {MB} = overrightarrow {DM} + overrightarrow {MC} \ Leftrightarrow – overrightarrow {MA} + overrightarrow {MB} = – overrightarrow {MD} + overrightarrow {MC} \ Leftrightarrow overrightarrow {MA} + overrightarrow {MC} = overrightarrow {MB} + overrightarrow {MD} end{array})
Cách 2:
Ta có: (overrightarrow {MA} + overrightarrow {MC} = overrightarrow {MB} + overrightarrow {MD} Leftrightarrow overrightarrow {MA} – overrightarrow {MB} = overrightarrow {MD} – overrightarrow {MC} ) (*)
Áp dụng quy tắc hiệu ta có: (overrightarrow {MA} – overrightarrow {MB} = overrightarrow {BA} ;;;overrightarrow {MD} – overrightarrow {MC} = overrightarrow {CD} )
Do đó (*) ( Leftrightarrow overrightarrow {BA} = overrightarrow {CD} ) (luôn đúng do ABCD là hình bình hành)
Cách 3:
Ta có:
adsense
(overrightarrow {MA} + overrightarrow {MC} = overrightarrow {MB} + overrightarrow {BA} + overrightarrow {MD} + overrightarrow {DC} = overrightarrow {MB} + overrightarrow {MD} + left( {overrightarrow {BA} + overrightarrow {DC} } right))
Vì ABCD là hình bình hành nên (overrightarrow {AB} = overrightarrow {DC} )( Rightarrow – overrightarrow {BA} = overrightarrow {DC} ) hay (overrightarrow {BA} + overrightarrow {DC} = overrightarrow 0 )
( Rightarrow overrightarrow {MA} + overrightarrow {MC} = overrightarrow {MB} + overrightarrow {MD} ) (đpcm)
Giải bài 4.35 trang 72 SGK Toán 10 Kết nối tri thức tập 1
Trong mặt phẳng tọa độ Oxy, cho A (2; 1), B (-2; 5) và C (-5; 2).
a) Tìm tọa độ của các vectơ (overrightarrow {BA} ) và (overrightarrow {BC} )
b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.
Phương pháp giải
a) Tọa độ của vectơ: (overrightarrow {BA} = ({x_A} – {x_B};{y_A} – {y_B}))
b) Tính (overrightarrow {BA} .overrightarrow {BC} =0 ), chỉ ra góc vuông trong tam giác ABC.
c) Công thức tọa độ của trọng tâm G là (left( {frac{{{x_A} + {x_B} + {x_C}}}{3};frac{{{y_A} + {y_B} + {y_C}}}{3}} right))
d) BCAD là một hình bình hành ( Leftrightarrow overrightarrow {BC} = overrightarrow {AD} )
Hướng dẫn giải
a) Ta có: (overrightarrow {BA} = (2 – ( – 2);1 – 5) = (4; – 4)) và (overrightarrow {BC} = ( – 5 – ( – 2);2 – 5) = ( – 3; – 3))
b)
Ta có: (overrightarrow {BA} .overrightarrow {BC} = 4.( – 3) + ( – 4).( – 3) = 0)
( Rightarrow overrightarrow {BA} bot overrightarrow {BC} ) hay (widehat {ABC} = {90^o})
Vậy tam giác ABC vuông tại B.
Lại có: (AB = left| {overrightarrow {BA} } right| = sqrt {{4^2} + {{( – 4)}^2}} = 4sqrt 2 ); (BC = left| {overrightarrow {BC} } right| = sqrt {{3^2} + {{( – 3)}^2}} = 3sqrt 2 )
Và (AC = sqrt {A{B^2} + B{C^2}} = 5sqrt 2 ) (do (Delta ABC)vuông tại B).
Diện tích tam giác ABC là: ({S_{ABC}} = frac{1}{2}.AB.BC = frac{1}{2}.4sqrt 2 .3sqrt 2 = 12)
Chu vi tam giác ABC là: (AB + BC + AC = 4sqrt 2 + 3sqrt 2 + 5sqrt 2 = 12sqrt 2 )
c) Tọa độ của trọng tâm G là (left( {frac{{2 + ( – 2) + ( – 5)}}{3};frac{{1 + 5 + 2}}{3}} right) = left( {frac{{ – 5}}{3};frac{8}{3}} right))
d) Giả sử điểm D thỏa mãn BCAD là một hình bình hành có tọa độ là (a; b).
Ta có: (overrightarrow {BC} = ( – 3; – 3)) và (overrightarrow {AD} = (a – 2;b – 1))
Vì BCAD là một hình bình hành nên (overrightarrow {AD} = overrightarrow {BC} )
(begin{array}{l} Leftrightarrow (a – 2;b – 1) = ( – 3; – 3)\ Leftrightarrow left{ begin{array}{l}a – 2 = – 3\b – 1 = – 3end{array} right. Leftrightarrow left{ begin{array}{l}a = – 1\b = – 2end{array} right.end{array})
Vậy D có tọa độ (-1; -2)
Giải bài 4.36 trang 72 SGK Toán 10 Kết nối tri thức tập 1
Trong mặt phẳng tọa độ Oxy, cho A (1; 2), B (3; 4), C (-2; -2) và D (6;5).
a) Hãy tìm tọa độ của các vectơ (overrightarrow {AB} ) và (overrightarrow {CD} )
b) Hãy giải thích tại sao các vectơ (overrightarrow {AB} ) và (overrightarrow {CD} ) cùng phương.
c) Giả sử E là điểm có tọa độ (a; 1). Tìm a để các vectơ (overrightarrow {AC} ) và (overrightarrow {BE} ) cùng phương.
d) Với a tìm được, hãy biểu thị vectơ (overrightarrow {AE} ) theo các vectơ (overrightarrow {AB} ) và (overrightarrow {AC} ).
Phương pháp giải
a) Tọa độ của vectơ: (overrightarrow {AB} = ({x_B} – {x_A};{y_B} – {y_A}))
b) Tìm (k ne 0) sao cho: (overrightarrow {AB} = k.overrightarrow {CD} )
c) Vectơ (overrightarrow u ,(a;b)) và (overrightarrow v ,(x;y))((x;y ne 0)) cùng phương ( Leftrightarrow frac{a}{x} = frac{b}{y}) ((x;y ne 0))
Hướng dẫn giải
a) Ta có: (overrightarrow {AB} = (3 – 1;4 – 2) = (2;2)) và (overrightarrow {CD} = (6 – ( – 1);5 – ( – 2)) = (7;7))
b) Dễ thấy: ((2;2) = frac{2}{7}.(7;7))( Rightarrow overrightarrow {AB} = frac{2}{7}.overrightarrow {CD} )
Vậy hai vectơ (overrightarrow {AB} ) và (overrightarrow {CD} ) cùng phương.
c) Ta có: (overrightarrow {AC} = ( – 1 – 1; – 2 – 2) = ( – 2; – 4)) và (overrightarrow {BE} = (a – 3;1 – 4) = (a – 3; – 3))
Để (overrightarrow {AC} ) và (overrightarrow {BE} ) cùng phương thì (frac{{a – 3}}{{ – 2}} = frac{{ – 3}}{{ – 4}})( Leftrightarrow a – 3 = – frac{3}{2})( Leftrightarrow a = frac{3}{2})
Vậy (a = frac{3}{2}) hay (Eleft( {frac{3}{2};1} right)) thì hai vectơ (overrightarrow {AC} ) và (overrightarrow {BE} ) cùng phương
Cách 1:
Ta có: (overrightarrow {BE} = left( {frac{3}{2} – 3; – 3} right) = left( { – frac{3}{2}; – 3} right)) ; (overrightarrow {AC} = ( – 2; – 4))
( Rightarrow overrightarrow {BE} = frac{3}{4}.overrightarrow {AC} )
Mà (overrightarrow {AE} = overrightarrow {AB} + overrightarrow {BE} ) (quy tắc cộng)
( Rightarrow overrightarrow {AE} = overrightarrow {AB} + frac{3}{4}.overrightarrow {AC} )
Cách 2:
Giả sử (overrightarrow {AE} = m,.,overrightarrow {AB} + n,.,overrightarrow {AC} )(*)
Ta có: (overrightarrow {AE} = left( {frac{1}{2}; – 1} right)), (m,.,overrightarrow {AB} = mleft( {2;2} right) = (2m;2m)), (n,.,overrightarrow {AC} = n( – 2; – 4) = ( – 2n; – 4n))
Do đó (*) ( Leftrightarrow left( {frac{1}{2}; – 1} right) = (2m;2m) + ( – 2n; – 4n))
(begin{array}{l} Leftrightarrow left( {frac{1}{2}; – 1} right) = (2m – 2n;2m – 4n)\ Leftrightarrow left{ begin{array}{l}frac{1}{2} = 2m – 2n\ – 1 = 2m – 4nend{array} right. Leftrightarrow left{ begin{array}{l}m = 1\n = frac{3}{4}end{array} right.end{array})
Vậy (overrightarrow {AE} = overrightarrow {AB} + frac{3}{4}.overrightarrow {AC} )
Giải bài 4.37 trang 72 SGK Toán 10 Kết nối tri thức tập 1
Cho vectơ (overrightarrow a ne overrightarrow 0 ). Chứng minh rằng (frac{1}{{|overrightarrow a |}};overrightarrow a ) (hay còn được viết là (frac{{overrightarrow a }}{{|overrightarrow a |}})) là một vectơ đơn vị, cùng hướng với vectơ (overrightarrow a ).
Phương pháp giải
Nhắc lại kiến thức: k(vec a) cùng hướng với (vec a)
nếu k > 0.
Ta có: (k = frac{1}{{left| {vec a} right|}} > 0left( {vec a ne vec 0} right))
Do đó (frac{1}{{left| {vec a} right|}}.vec a) cùng hướng với (vec a) hay (frac{{vec a}}{{left| {vec a} right|}}) cùng hướng với (vec a)
Hướng dẫn giải
Gọi tọa độ của vectơ (overrightarrow a ) là (x; y).
Ta có: (|overrightarrow a |, = sqrt {{x^2} + {y^2}} ).
Đặt (overrightarrow i = frac{1}{{|overrightarrow a |}};.overrightarrow a )
( Rightarrow overrightarrow i = frac{1}{{sqrt {{x^2} + {y^2}} }}.(x;y) = left( {frac{x}{{sqrt {{x^2} + {y^2}} }};frac{y}{{sqrt {{x^2} + {y^2}} }}} right))
( Rightarrow |overrightarrow i |, = sqrt {{{left( {frac{x}{{sqrt {{x^2} + {y^2}} }}} right)}^2} + {{left( {frac{y}{{sqrt {{x^2} + {y^2}} }}} right)}^2}} = sqrt {frac{{{x^2}}}{{{x^2} + {y^2}}} + frac{{{y^2}}}{{{x^2} + {y^2}}}} = 1)
Mặt khác:
(overrightarrow i = frac{1}{{|overrightarrow a |}};.overrightarrow a = frac{1}{{sqrt {{x^2} + {y^2}} }}.overrightarrow a ) và (frac{1}{{sqrt {{x^2} + {y^2}} }} > 0) với mọi (x,y ne 0)
Do đó vectơ (overrightarrow i ) và (overrightarrow a ) cùng hướng.
Vậy (frac{1}{{|overrightarrow a |}};overrightarrow a ) (hay (frac{{overrightarrow a }}{{|overrightarrow a |}})) là một vectơ đơn vị, cùng hướng với vectơ (overrightarrow a ).
Cách 2:
Với mọi vectơ (overrightarrow a ne overrightarrow 0 ), ta có: (|overrightarrow a |; > 0 Rightarrow k = frac{1}{{|overrightarrow a |}} > 0). Đặt (overrightarrow i = frac{1}{{|overrightarrow a |}};.overrightarrow a = k.overrightarrow a )
(begin{array}{l} Rightarrow |overrightarrow i |, = ;|k.overrightarrow a |; = ;|k|.|overrightarrow a |;\ Leftrightarrow left| {overrightarrow {,i} ,} right| = k.|overrightarrow a |; = frac{1}{{|overrightarrow a |}}.|overrightarrow a | = 1end{array})
Mặt khác: (overrightarrow i = frac{1}{{|overrightarrow a |}};.overrightarrow a = k.overrightarrow a ) và (k > 0)
Do đó vectơ (overrightarrow i ) và (overrightarrow a ) cùng hướng.
Vậy (frac{1}{{|overrightarrow a |}};overrightarrow a ) (hay (frac{{overrightarrow a }}{{|overrightarrow a |}})) là một vectơ đơn vị, cùng hướng với vectơ (overrightarrow a ).
Giải bài 4.38 trang 72 SGK Toán 10 Kết nối tri thức tập 1
Cho ba vectơ (overrightarrow a ,;overrightarrow b ,;overrightarrow u ) với (|overrightarrow a |; = ;,|overrightarrow b |; = 1) và (overrightarrow a bot overrightarrow b ). Xét một hệ trục Oxy với các vectơ đơn vị (overrightarrow i = overrightarrow a ,;overrightarrow j = overrightarrow b .) Chứng minh rằng:
a) Vectơ (overrightarrow u ) có tọa độ là ((overrightarrow u ,.,overrightarrow a ,;,overrightarrow u ,.,overrightarrow b ))
b) (overrightarrow u = (overrightarrow u ,.,overrightarrow a ,).overrightarrow a + (,overrightarrow u ,.,overrightarrow b ).overrightarrow b )
Phương pháp giải
a) Trên hệ trục Oxy mới, xác định hoành độ, tung độ của vectơ (overrightarrow u )
+) (overrightarrow u ,.,overrightarrow a = |overrightarrow u| ,.,|overrightarrow a|. cos(overrightarrow u ,.,overrightarrow a) )
b) Vectơ (overrightarrow u ) có tọa độ ((x,;y)) trong hệ trục Oxy với các vectơ đơn vị (overrightarrow i ;;overrightarrow j ) thì (overrightarrow u = x,.,overrightarrow i + y.,overrightarrow j )
Hướng dẫn giải
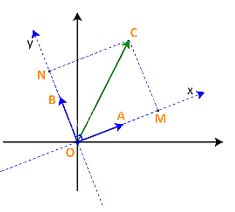
a) Trên mặt phẳng tọa độ, lấy các điểm A, B, C sao cho (overrightarrow {OA} = overrightarrow a ;;overrightarrow {OB} = overrightarrow b ;;overrightarrow {OC} = overrightarrow u )
Trên hệ trục Oxy với các vectơ đơn vị (overrightarrow i = overrightarrow a ,;overrightarrow j = overrightarrow b ), lấy M, N là hình chiếu của C trên Ox, Oy.
Gọi tọa độ của (overrightarrow u )là (left( {x;y} right)). Đặt (alpha = left( {overrightarrow u ,overrightarrow a } right)).
+) Nếu ({0^o} < alpha < {90^o}): (x = OM = ;|overrightarrow u |.cos alpha = ;|overrightarrow u |.cos alpha .;|overrightarrow a |; = overrightarrow u ,.,overrightarrow a ,;)
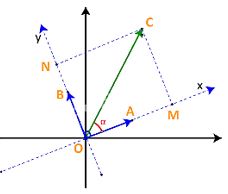
+) Nếu ({90^o} < alpha < {180^o}): (x = – OM = ; – |overrightarrow u |.cos ({180^o} – alpha ) = ;|overrightarrow u |.cos alpha ; = overrightarrow u ,.,overrightarrow a ,;)
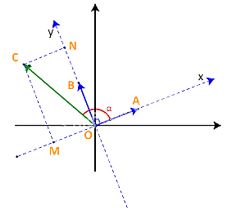
Như vậy ta luôn có: (x = overrightarrow u .overrightarrow a )
Chứng minh tương tự, ta có: (y = overrightarrow u .overrightarrow b )
Vậy vectơ (overrightarrow u ) có tọa độ là ((overrightarrow u ,.,overrightarrow a ,;,overrightarrow u ,.,overrightarrow b ))
b) Trong hệ trục Oxy với các vectơ vectơ đơn vị (overrightarrow i = overrightarrow a ,;overrightarrow j = overrightarrow b ), vectơ (overrightarrow u ) có tọa độ là ((overrightarrow u ,.,overrightarrow a ,;,overrightarrow u ,.,overrightarrow b ))
(begin{array}{l} Rightarrow overrightarrow u = (overrightarrow u ,.,overrightarrow a ,).overrightarrow i + (,overrightarrow u ,.,overrightarrow b ).overrightarrow j \ Leftrightarrow overrightarrow u = (overrightarrow u ,.,overrightarrow a ,).overrightarrow a + (,overrightarrow u ,.,overrightarrow b ).overrightarrow b end{array})
Giải bài 4.39 trang 72 SGK Toán 10 Kết nối tri thức tập 1
Trên sông, một cano chuyển động thẳng đều theo hướng (S{15^o}E) với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.
Phương pháp giải
Định lí cosin trong tam giác OAC: (A{C^2} = O{A^2} + O{C^2} – 2.OA.OC.cos widehat {AOC})
Hướng dẫn giải
Lấy các điểm: A, C sao cho:
Vectơ vận tốc dòng nước(overrightarrow {{v_n}} = overrightarrow {OA} )
Vectơ vận tốc chuyển động (overrightarrow {{v_{cano}}} = overrightarrow {OC} )
Ta có: (overrightarrow {{v_{cano}}} = overrightarrow {{v_n}} + overrightarrow v ), với (overrightarrow v ) là vectơ vận tốc riêng của cano.
Gọi B là điểm sao cho (overrightarrow v = overrightarrow {OB} ) thì OACB là hình bình hành.
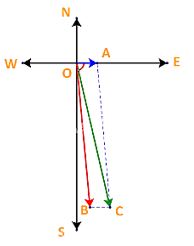
Vì tàu chuyển động theo hướng (S{15^o}E) nên vectơ (overrightarrow {OC} ) tạo với hướng Nam (tia OS) góc ({15^o}) và tạo với hướng Đông (tia OE) góc ({90^o} – {15^o} = {75^o}).
Mà nước trên sông chảy về hướng đông nên vectơ (overrightarrow {OA} ) cùng hướng với vectơ (overrightarrow {OE} )
Do đó góc tạo bởi vectơ (overrightarrow {OC} ) và vectơ (overrightarrow {OA} ) là ({75^o})
Xét tam giác OAC ta có:
(OA = ;|overrightarrow {{v_n}} |; = 3); (OC = ;|overrightarrow {{v_{cano}}} |; = 20) và (widehat {AOC} = {75^o})
Áp dụng định lí cosin tại đỉnh O ta được:
(begin{array}{l}A{C^2} = O{A^2} + O{C^2} – 2.OA.OC.cos widehat {AOC}\ Leftrightarrow A{C^2} = {3^2} + {20^2} – 2.3.20.cos {75^o} approx 378\ Leftrightarrow OB = AC approx 19,44end{array})
Vậy vận tốc riêng của cano là 19,44 km/h
