adsense
GIẢI SGK Bài 1. Dãy số – Toán 11 CTST
===========
Bài 1 trang 50 SGK Toán 11 tập 1 – CTST
Đề bài
Tìm \({u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\) của dãy số:
\(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = \frac{{{u_n}}}{{1 + {u_n}}}\left( {n \ge 1} \right)\end{array} \right.\)
‒ Lần lượt thay giá trị \(n = 1;2;3\) vào biểu thức \({u_{n + 1}}\).
‒ Tìm điểm chung của các số hạng của dãy số \(\left( {{u_n}} \right)\).
Lời giải chi tiết
Ta có:
\(\begin{array}{l}{u_2} = \frac{{{u_1}}}{{1 + {u_1}}} = \frac{1}{{1 + 1}} = \frac{1}{2}\\{u_3} = \frac{{{u_2}}}{{1 + {u_2}}} = \frac{{\frac{1}{2}}}{{1 + \frac{1}{2}}} = \frac{1}{3}\end{array}\)
Suy ra, \({u_n} = \frac{1}{n}\)
Bài 2 trang 50 SGK Toán 11 tập 1 – CTST
Đề bài
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + … + \frac{1}{{n\left( {n + 1} \right)}}\). Tìm \({u_1},{u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\).
‒ Lần lượt thay giá trị \(n = 1;2;3\) vào biểu thức \({u_n}\).
‒ Tìm điểm chung của các số hạng của dãy số \(\left( {{u_n}} \right)\).
Lời giải chi tiết
\(\begin{array}{l}{u_1} = \frac{1}{{1.2}} = \frac{1}{2}\\{u_2} = \frac{1}{{1.2}} + \frac{1}{{2.3}} = \frac{2}{3}\\{u_3} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} = \frac{3}{4}\\{u_n} = \frac{n}{{n + 1}}\end{array}\)
Bài 3 trang 50 SGK Toán 11 tập 1 – CTST
Đề bài
Xét tính tăng, giảm của dãy số \(\left( {{y_n}} \right)\) với \({y_n} = \sqrt {n + 1} – \sqrt n \).
Bước 1: Tìm \({y_{n + 1}}\).
Bước 2: Xét hiệu \({y_{n + 1}} – {y_n}\) hoặc xét thương \(\frac{{{y_{n + 1}}}}{{{y_n}}}\) nếu các số hạng của dãy số \(\left( {{y_n}} \right)\) là số dương.
Bước 3: Kết luận:
– Nếu \({y_{n + 1}} – {y_n} > 0\) hoặc \(\frac{{{y_{n + 1}}}}{{{y_n}}} > 1\) thì \({y_{n + 1}} > {y_n},\forall n \in {\mathbb{N}^*}\), vậy dãy số \(\left( {{y_n}} \right)\) là dãy số tăng.
– Nếu \({y_{n + 1}} – {y_n} < 0\) hoặc \(\frac{{{y_{n + 1}}}}{{{y_n}}} < 1\) thì \({y_{n + 1}} < {y_n},\forall n \in {\mathbb{N}^*}\), vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.
Lời giải chi tiết
Cách 1:
Ta có: \({y_n} = \sqrt {n + 1} – \sqrt n = \frac{{\left( {\sqrt {n + 1} – \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {n + 1} \right) – n}}{{\sqrt {n + 1} + \sqrt n }} = \frac{1}{{\sqrt {n + 1} + \sqrt n }}\)
\( \Rightarrow {y_{n + 1}} = \frac{1}{{\sqrt {\left( {n + 1} \right) + 1} – \sqrt {n + 1} }} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }}\)
Xét hiệu:
\(\begin{array}{l}{y_{n + 1}} – {y_n} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }} – \frac{1}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {\sqrt {n + 1} + \sqrt n } \right) – \left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)}}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}\\ = \frac{{\sqrt {n + 1} + \sqrt n – \sqrt {n + 2} – \sqrt {n + 1} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}} = \frac{{\sqrt n – \sqrt {n + 2} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}\end{array}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(\begin{array}{l}\left. \begin{array}{l}0 < n < n + 2 \Leftrightarrow \sqrt n < \sqrt {n + 2} \Leftrightarrow \sqrt n – \sqrt {n + 2} < 0\\\sqrt {n + 2} > 0,\sqrt {n + 1} > 0,\sqrt n > 0 \Leftrightarrow \left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right) > 0\end{array} \right\}\\ \Rightarrow \frac{{\sqrt n – \sqrt {n + 2} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}} < 0\end{array}\)
Vậy \({y_{n + 1}} – {y_n} < 0 \Leftrightarrow {y_{n + 1}} < {y_n}\). Vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.
Cách 2:
Ta có: \({y_n} = \sqrt {n + 1} – \sqrt n = \frac{{\left( {\sqrt {n + 1} – \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {n + 1} \right) – n}}{{\sqrt {n + 1} + \sqrt n }} = \frac{1}{{\sqrt {n + 1} + \sqrt n }}\)
\( \Rightarrow {y_{n + 1}} = \frac{1}{{\sqrt {\left( {n + 1} \right) + 1} – \sqrt {n + 1} }} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(\begin{array}{l}0 < n < n + 2 \Leftrightarrow \sqrt n < \sqrt {n + 2} \Leftrightarrow \sqrt {n + 1} + \sqrt n < \sqrt {n + 2} + \sqrt {n + 1} \\ \Leftrightarrow \frac{1}{{\sqrt {n + 1} + \sqrt n }} > \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }} \Leftrightarrow {y_n} > {y_{n + 1}}\end{array}\)
Vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.
Bài 4 trang 50 SGK Toán 11 tập 1 – CTST
Đề bài
Xét tính bị chặn của các dãy số sau:
a) \(\left( {{a_n}} \right)\) với \({a_n} = {\sin ^2}\frac{{n\pi }}{3} + \cos \frac{{n\pi }}{4}\);
b) \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{6n – 4}}{{n + 2}}\)
a) Sử dụng tính chất của hàm lượng giác.
b) Sử dụng tính chất của bất đẳng thức.
Lời giải chi tiết
a) \(\forall n \in {\mathbb{N}^*}\) ta có:
\(\left. \begin{array}{l}0 \le {\sin ^2}\frac{{n\pi }}{3} \le 1\\ – 1 \le \cos \frac{{n\pi }}{4} \le 1\end{array} \right\} \Leftrightarrow 0 + \left( { – 1} \right) \le {\sin ^2}\frac{{n\pi }}{3} + \cos \frac{{n\pi }}{4} \le 1 + 1 \Leftrightarrow – 1 \le {a_n} \le 2\).
Vậy dãy số \(\left( {{a_n}} \right)\) bị chặn.
b) Ta có: \({u_n} = \frac{{6n – 4}}{{n + 2}} = \frac{{6\left( {n + 2} \right) – 16}}{{n + 2}} = 6 – \frac{{16}}{{n + 2}}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
adsense
\(n + 2 > 0 \Leftrightarrow \frac{{16}}{{n + 2}} > 0 \Leftrightarrow 6 – \frac{{16}}{{n + 2}} < 6 \Leftrightarrow {u_n} < 6\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.
\(n \ge 1 \Leftrightarrow n + 2 \ge 1 + 2 \Leftrightarrow n + 2 \ge 3 \Leftrightarrow \frac{{16}}{{n + 2}} \le \frac{{16}}{3} \Leftrightarrow 6 – \frac{{16}}{{n + 2}} \ge 6 – \frac{{16}}{3} \Leftrightarrow {u_n} \ge \frac{2}{3}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.
Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.
Bài 5 trang 50 SGK Toán 11 tập 1 – CTST
Đề bài
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n – 1}}{{n + 1}}\).
Chứng minh \(\left( {{u_n}} \right)\) là dãy số tăng và bị chặn.
• Chứng minh \(\left( {{u_n}} \right)\) là dãy số tăng:
Bước 1: Tìm \({u_{n + 1}}\).
Bước 2: Xét hiệu \({u_{n + 1}} – {u_n}\).
Bước 3: Chứng minh \({u_{n + 1}} – {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n},\forall n \in {\mathbb{N}^*}\), từ đó kết luận dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.
• Chứng minh \(\left( {{u_n}} \right)\) bị chặn: Sử dụng tính chất của bất đẳng thức.
Lời giải chi tiết
• Ta có: \({u_{n + 1}} = \frac{{2\left( {n + 1} \right) – 1}}{{\left( {n + 1} \right) + 1}} = \frac{{2n + 2 – 1}}{{n + 1 + 1}} = \frac{{2n + 1}}{{n + 2}}\)
Xét hiệu:
\(\begin{array}{l}{u_{n + 1}} – {u_n} = \frac{{2n + 1}}{{n + 2}} – \frac{{2n – 1}}{{n + 1}} = \frac{{\left( {2n + 1} \right)\left( {n + 1} \right) – \left( {2n – 1} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{\left( {2{n^2} + n + 2n + 1} \right) – \left( {2{n^2} – n + 4n – 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{2{n^2} + n + 2n + 1 – 2{n^2} + n – 4n + 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{3}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}\)
Vậy \({u_{n + 1}} – {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\). Vậy dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.
• Ta có: \({u_n} = \frac{{2n – 1}}{{n + 1}} = \frac{{2\left( {n + 1} \right) – 3}}{{n + 1}} = 2 – \frac{3}{{n + 1}}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(n + 1 > 0 \Leftrightarrow \frac{3}{{n + 1}} > 0 \Leftrightarrow 2 – \frac{3}{{n + 1}} < 2 \Leftrightarrow {u_n} < 2\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.
\(n \ge 1 \Leftrightarrow n + 1 \ge 1 + 1 \Leftrightarrow n + 1 \ge 2 \Leftrightarrow \frac{3}{{n + 1}} \le \frac{3}{2} \Leftrightarrow 2 – \frac{3}{{n + 1}} \ge 2 – \frac{3}{2} \Leftrightarrow {u_n} \ge \frac{1}{2}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.
Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.
Bài 6 trang 50 SGK Toán 11 tập 1 – CTST
Đề bài
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{na + 2}}{{n + 1}}\). Tìm giá trị của \(a\) để:
a) \(\left( {{u_n}} \right)\) là dãy số tăng;
b) \(\left( {{u_n}} \right)\) là dãy số giảm.
Bước 1: Tìm \({u_{n + 1}}\).
Bước 2: Xét hiệu \({u_{n + 1}} – {u_n}\).
Bước 3:
– Để \(\left( {{u_n}} \right)\) là dãy số tăng thì ta tìm \(a\) sao cho \({u_{n + 1}} – {u_n} > 0,\forall n \in {\mathbb{N}^*}\).
– Để \(\left( {{u_n}} \right)\) là dãy số giảm thì ta tìm \(a\) sao cho \({u_{n + 1}} – {u_n} < 0,\forall n \in {\mathbb{N}^*}\).
Lời giải chi tiết
Ta có: \({u_{n + 1}} = \frac{{\left( {n + 1} \right)a + 2}}{{\left( {n + 1} \right) + 1}} = \frac{{na + a + 2}}{{n + 1 + 1}} = \frac{{na + a + 2}}{{n + 2}}\)
Xét hiệu:
\(\begin{array}{l}{u_{n + 1}} – {u_n} = \frac{{na + a + 2}}{{n + 2}} – \frac{{na + 2}}{{n + 1}} = \frac{{\left( {na + a + 2} \right)\left( {n + 1} \right) – \left( {na + 2} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{\left( {{n^2}a + na + 2n + na + a + 2} \right) – \left( {{n^2}a + 2n + 2na + 4} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{{n^2}a + na + 2n + na + a + 2 – {n^2}a – 2n – 2na – 4}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{{a – 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\end{array}\)
a) Để \(\left( {{u_n}} \right)\) là dãy số tăng thì:
\({u_{n + 1}} – {u_n} > 0,\forall n \in {\mathbb{N}^*} \Leftrightarrow \frac{{a – 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0 \Leftrightarrow a – 2 > 0 \Leftrightarrow a > 2\)
b) Để \(\left( {{u_n}} \right)\) là dãy số giảm thì:
\({u_{n + 1}} – {u_n} < 0,\forall n \in {\mathbb{N}^*} \Leftrightarrow \frac{{a – 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} < 0 \Leftrightarrow a – 2 < 0 \Leftrightarrow a < 2\)
Bài 7 trang 50 SGK Toán 11 tập 1 – CTST
Đề bài
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
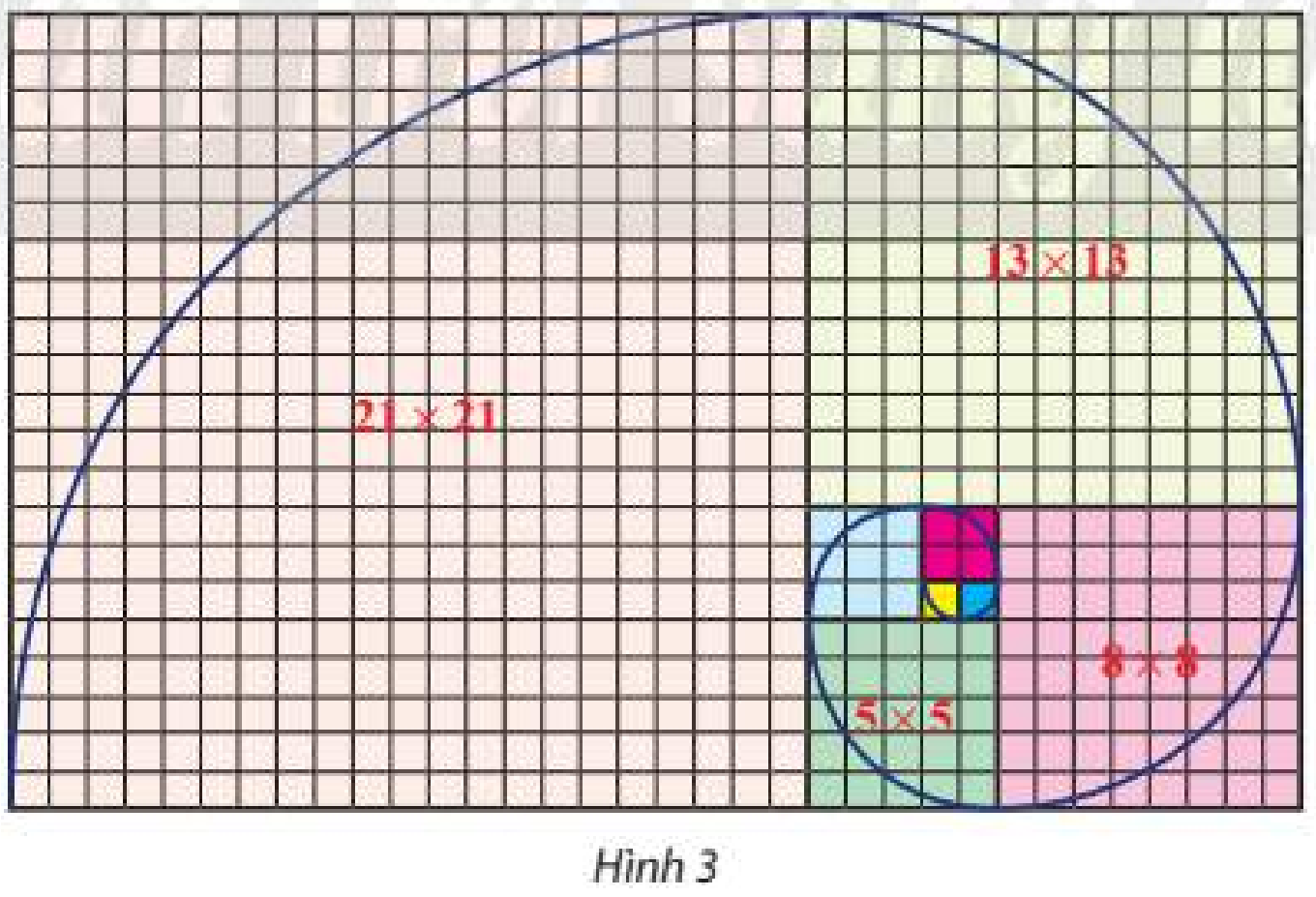
Dựa vào hình vẽ, tìm độ dài cạnh của các hình vuông theo thứ tự từ nhỏ đến lớn.
Lời giải chi tiết
Ta có: \({u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21\)
Ta có:
\(\begin{array}{l}{u_3} = 2 = {u_2} + {u_1}\\{u_4} = 3 = {u_3} + {u_2}\\{u_5} = 5 = {u_4} + {u_3}\\{u_6} = 8 = {u_5} + {u_4}\\{u_7} = 13 = {u_6} + {u_5}\\{u_8} = 21 = {u_7} + {u_6}\end{array}\)
Ta thấy dãy số này kể từ số hạng thứ 3 bằng tổng của hai số hạng đứng trước nó.
Vậy dãy số này có công thức truy hồi là:
\(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n – 1}} + {u_{n – 2}}\left( {n \ge 3} \right)\end{array} \right.\)
