adsense
Giải SGK Bài tập cuối chương 1 – Toán 11 CD
=========
Bài 1 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Hàm số y = sinx đồng biến trên khoảng:
A. \(\left( {0;\pi } \right)\)
B. \(\left( { – \frac{{3\pi }}{2}; – \frac{\pi }{2}} \right)\)
C. \(\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)\)
D. \(\left( { – \pi ;0} \right)\)
Sử dụng khoảng biến thiên của hàm số y = sinx
Lời giải chi tiết
Hàm số y = sinx đồng biến trên khoảng: \(\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)\)
Chọn C
Bài 2 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Hàm số nghịch biến trên khoảng \(\left( {\pi ;2\pi } \right)\) là:
A.\(y = \sin x\)
B.\(y = \cos x\)
C.\(y = \tan x\)
D.\(y = \cot x\)
Sử dụng khoảng biến thiên của các hàm số lượng giác
Lời giải chi tiết
Hàm số nghịch biến trên khoảng \(\left( {\pi ;2\pi } \right)\) là:\(y = \cos x\)
Chọn B
Bài 3 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Nếu \(\tan \left( {a + b} \right) = 3,\tan \left( {a – b} \right) = – 3\) thì \(\tan 2a\) bằng:
A.0
B.\(\frac{3}{5}\)
C.1
D.\( – \frac{3}{4}\)
Sử dụng công thức lương giác của tan.
Lời giải chi tiết
Ta có :
\(\begin{array}{l}\tan \left( {a + b} \right) = 3\\ \Rightarrow \frac{{tana + \tan b}}{{1 – \tan a.\tan b}} = 3\\ \Rightarrow tana + \tan b = 3(1 – \tan a.\tan b)\,\,\,\,\,\,(1)\\\tan \left( {a – b} \right) = – 3\\ \Rightarrow \frac{{tana – \tan b}}{{1 + \tan a.\tan b}} = 3\\ \Rightarrow tana – \tan b = 3(1 + \tan a.\tan b)\,\,\,\,\,\,(2)\end{array}\)
Cộng theo vế của (1) và (2) ta có
\(\tan a = 3\)
Ta có
\(\tan 2a = \frac{{2\tan a}}{{1 – {{\tan }^2}a}} = \frac{{2.3}}{{1 – {3^2}}} = \frac{{ – 3}}{4}\)
Chọn D
Bài 4 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Nếu \(\cos a = \frac{1}{4}\) thì \(\cos 2a\) bằng:
A.\(\frac{7}{8}\)
B.\( – \frac{7}{8}\)
C.\(\frac{{15}}{{16}}\)
D.\( – \frac{{15}}{{16}}\)
Sử dụng công thức nhân đôi
Lời giải chi tiết
Ta có \(\cos 2a = 2{\cos ^2}a – 1 = 2.{\left( {\frac{1}{4}} \right)^2} – 1 = \frac{{ – 7}}{8}\)
Chọn B
Bài 5 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Nếu \(\cos a = \frac{3}{5}\) và \(\cos b = – \frac{4}{5}\) thì \(\cos \left( {a + b} \right)\cos \left( {a – b} \right)\) bằng:
A.0
B.2
C.4
D.5
Sử dụng công thức biến đổi tích thành tổng
Lời giải chi tiết
Ta có :
\(\cos \left( {a + b} \right)\cos \left( {a – b} \right) = \frac{1}{2}\left( {\cos 2a + \cos 2b} \right) = \frac{1}{2}\left( {2{{\cos }^2}a – 1 + 2{{\cos }^2}b – 1} \right) = 0\)
Chọn A
Bài 6 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Nếu \(\sin a = – \frac{{\sqrt 2 }}{3}\) thì \(\sin \left( {a + \frac{\pi }{4}} \right) + \sin \left( {a – \frac{\pi }{4}} \right)\) bằng
A.\(\frac{2}{3}\)
B.\(\frac{1}{3}\)
C.\( – \frac{2}{3}\)
D.\( – \frac{1}{3}\)
Sử dụng công thức biến đổi tổng thành tích
Lời giải chi tiết
Ta có :
\(\sin \left( {a + \frac{\pi }{4}} \right) + \sin \left( {a – \frac{\pi }{4}} \right) = 2.\sin a.\cos \frac{\pi }{4} = – \frac{2}{3}\)
Chọn C
Bài 7 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Số nghiệm của phương trình cosx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là
A.5
B.9
C.10
D.11
Sử dụng công thức tổng quát của phương trình cos
Lời giải chi tiết
Ta có
\(\begin{array}{l}cosx{\rm{ }} = {\rm{ }}0\\ \Leftrightarrow cosx{\rm{ }} = {\rm{ cos}}\frac{\pi }{2}\\ \Leftrightarrow x{\rm{ }} = {\rm{ }}\frac{\pi }{2} + k\pi ;k \in Z\end{array}\)
Mà \(x \in \left[ {0;10\pi } \right]\) nên
\(\begin{array}{l}0 \le \frac{\pi }{2} + k\pi \le 10\pi \\ \Rightarrow – 0,5 \le k \le 9,5\end{array}\)
Lại có \(k \in Z\) suy ra \(k \in \left\{ {0;1;2;3;4;5;6;7;8;9} \right\}\)
Vậy phương trình đã cho có số nghiệm là 10.
Chọn C
Bài 8 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Số nghiệm của phương trình sinx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là:
A.10
B.6
C.5
D.11
Sử dụng công thức tổng quát của phương trình sin
Lời giải chi tiết
Ta có
\(\begin{array}{l}\sin x{\rm{ }} = {\rm{ }}0\\ \Leftrightarrow \sin x{\rm{ }} = {\rm{ sin 0}}\\ \Leftrightarrow x{\rm{ }} = {\rm{ }}k\pi ;k \in Z\end{array}\)
Mà \(x \in \left[ {0;10\pi } \right]\) nên
\(\begin{array}{l}0 \le k\pi \le 10\pi \\ \Rightarrow 0 \le k \le 10\end{array}\)
Lại có \(k \in Z\) suy ra \(k \in \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)
Vậy phương trình đã cho có số nghiệm là 11.
Chọn D
Bài 9 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Phương trình \(\cot x = – 1\) có nghiệm là:
A.\( – \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
adsense
B.\(\frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
C.\(\frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
D.\( – \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
Sử dụng công thức tổng quát của phương trình cot
Lời giải chi tiết
Ta có
\(\begin{array}{l}\cot x{\rm{ }} = {\rm{ – 1}}\\ \Leftrightarrow \cot x{\rm{ }} = {\rm{ cot – }}\frac{\pi }{4}\\ \Leftrightarrow x{\rm{ }} = {\rm{ – }}\frac{\pi }{4} + k\pi ;k \in Z\end{array}\)
Vậy phương trình đã cho có nghiệm là \(x{\rm{ }} = {\rm{ – }}\frac{\pi }{4} + k\pi ;k \in Z\)
Chọn A
Bài 10 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Số nghiệm của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) trên đoạn \(\left[ {0;\pi } \right]\) là:
A.4
B.1
C.2
D.3
Sử dụng công thức tổng quát của phương trình sin
Lời giải chi tiết
Ta có
\(\begin{array}{l}\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\frac{\pi }{4} + k2\pi ;k \in Z\\x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\pi {\rm{ – }}\frac{\pi }{4} + k2\pi ;k \in Z\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {\rm{ }}k2\pi ;k \in Z\\x{\rm{ }} = {\rm{ }}\frac{\pi }{2} + k2\pi ;k \in Z\end{array} \right.\end{array}\)
Mà \(x \in \left[ {0;\pi } \right]\) nên \(x \in \left\{ {0;\frac{\pi }{2}} \right\}\)
Vậy phương trình đã cho có số nghiệm là 2.
Chọn C
Bài 11 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Vẽ đồ thị hàm số \(y = \cos x\) trên đoạn \(\left[ { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) rồi xác định số nghiệm của phương trình 3cosx + 2 = 0 trên đoạn đó.
Dựa vào vẽ đồ thị đã học để vẽ rồi xác định số nghiệm
Lời giải chi tiết
Vẽ đồ thị:
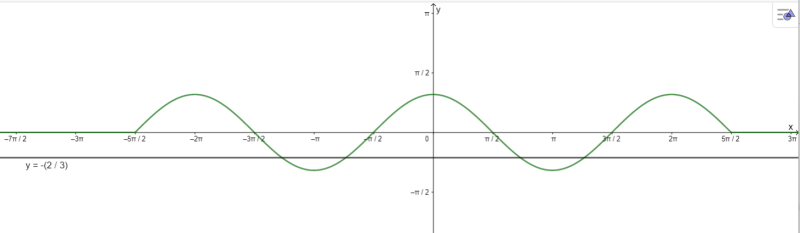
\(3\cos x + 2 = 0\) trên đoạn \(\left[ { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 4 nghiệm
Bài 12 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Giải các phương trình sau:
a) \(\sin \left( {2x – \frac{\pi }{6}} \right) = – \frac{{\sqrt 3 }}{2}\)
b) \(\cos \left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right) = \frac{1}{2}\)
c) \(\sin 3x – \cos 5x = 0\)
d) \({\cos ^2}x = \frac{1}{4}\)
e) \(\sin x – \sqrt 3 \cos x = 0\)
f) \(\sin x + \cos x = 0\)
Sử dụng các công thức nghiệm của phương trình lượng giác
Lời giải chi tiết
a)
\(\begin{array}{l}\sin \left( {2x – \frac{\pi }{6}} \right) = – \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow \sin \left( {2x – \frac{\pi }{6}} \right) = \sin \left( { – \frac{\pi }{3}} \right)\end{array}\)
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}2x – \frac{\pi }{6} = – \frac{\pi }{3} + k2\pi \\2x – \frac{\pi }{6} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x = – \frac{\pi }{6} + k2\pi \\2x = \frac{{3\pi }}{2} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = – \frac{\pi }{{12}} + k\pi \\x = \frac{{3\pi }}{4} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
b) \(\begin{array}{l}\cos \left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right) = \frac{1}{2}\\ \Leftrightarrow \cos \left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right) = \cos \frac{\pi }{3}\end{array}\)
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\frac{{3x}}{2} + \frac{\pi }{4} = \frac{\pi }{3} + k2\pi \\\frac{{3x}}{2} + \frac{\pi }{4} = \frac{{ – \pi }}{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{18}} + \frac{{k4\pi }}{3}\\x = \frac{{ – 7\pi }}{{18}} + \frac{{k4\pi }}{3}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
c)
\(\begin{array}{l}\sin 3x – \cos 5x = 0\\ \Leftrightarrow \sin 3x = \cos 5x\\ \Leftrightarrow \cos 5x = \cos \left( {\frac{\pi }{2} – 3x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}5x = \frac{\pi }{2} – 3x + k2\pi \\5x = – \left( {\frac{\pi }{2} – 3x} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}8x = \frac{\pi }{2} + k2\pi \\2x = – \frac{\pi }{2} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}\\x = – \frac{\pi }{4} + k\pi \end{array} \right.\end{array}\)
d)
\(\begin{array}{l}{\cos ^2}x = \frac{1}{4}\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = \frac{1}{2}\\\cos x = – \frac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = \cos \frac{\pi }{3}\\\cos x = \cos \frac{{2\pi }}{3}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = – \frac{\pi }{3} + k2\pi \end{array} \right.\\\left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = – \frac{{2\pi }}{3} + k2\pi \end{array} \right.\end{array} \right.\end{array}\)
e)
\(\begin{array}{l}\sin x – \sqrt 3 \cos x = 0\\ \Leftrightarrow \frac{1}{2}\sin x – \frac{{\sqrt 3 }}{2}\cos x = 0\\ \Leftrightarrow \cos \frac{\pi }{3}.\sin x – \sin \frac{\pi }{3}.\cos x = 0\\ \Leftrightarrow \sin \left( {x – \frac{\pi }{3}} \right) = 0\\ \Leftrightarrow \sin \left( {x – \frac{\pi }{3}} \right) = \sin 0\\ \Leftrightarrow x – \frac{\pi }{3} = k\pi ;k \in Z\\ \Leftrightarrow x = \frac{\pi }{3} + k\pi ;k \in Z\end{array}\)
f)
\(\begin{array}{l}\sin x + \cos x = 0\\ \Leftrightarrow \frac{{\sqrt 2 }}{2}\sin x + \frac{{\sqrt 2 }}{2}\cos x = 0\\ \Leftrightarrow \cos \frac{\pi }{4}.\sin x + \sin \frac{\pi }{4}.\cos x = 0\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = 0\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin 0\\ \Leftrightarrow x + \frac{\pi }{4} = k\pi ;k \in Z\\ \Leftrightarrow x = – \frac{\pi }{4} + k\pi ;k \in Z\end{array}\)
Bài 13 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày \(\left( {0 \le t < 24} \right)\) cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\). Tìm t để độ sâu của mực nước là
a) 15m
b) 9m
c) 10,5m
Sử dụng công thức nghiệm của phương trình hàm số cos
Lời giải chi tiết
+) Độ sâu của mực nước là 15m thì h = 15.
Khi đó
\(\begin{array}{l}15 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos 0\\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi – 1} \right)}}{\pi };k \in Z\end{array}\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {k2\pi – 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {2\pi – 1} \right)}}{\pi };\frac{{6\left( {4\pi – 1} \right)}}{\pi }} \right\}\)
+) Độ sâu của mực nước là 9m thì h = 9.
Khi đó
\(\begin{array}{l}9 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = – 1\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \pi \\ \Leftrightarrow \frac{{\pi t}}{6} + 1 = \pi + k2\pi \\ \Leftrightarrow t = \frac{{6\left( {k2\pi + \pi – 1} \right)}}{\pi };k \in Z\end{array}\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {k2\pi + \pi – 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 1\end{array}\)
Lại do \(k \in Z \Rightarrow k = 1 \Rightarrow t = \frac{{6\left( {3\pi – 1} \right)}}{\pi }\)
+) Độ sâu của mực nước là 10,5m thì h = 10,5.
Khi đó
\(\begin{array}{l}10,5 = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = – \frac{1}{2}\\ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = \cos \frac{{2\pi }}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{{\pi t}}{6} + 1 = \frac{{2\pi }}{3} + k2\pi \\\frac{{\pi t}}{6} + 1 = – \frac{{2\pi }}{3} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi – 1} \right)}}{\pi };k \in Z\\t = \frac{{6\left( { – \frac{{2\pi }}{3} + k2\pi – 1} \right)}}{\pi };k \in Z\end{array} \right.\end{array}\)
Với \(t = \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi – 1} \right)}}{\pi };k \in Z\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( {\frac{{2\pi }}{3} + k2\pi – 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 \le k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {0;1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( {\frac{{2\pi }}{3} – 1} \right)}}{\pi };\frac{{6\left( {\frac{{8\pi }}{3} – 1} \right)}}{\pi };\frac{{6\left( {\frac{{14\pi }}{3} – 1} \right)}}{\pi }} \right\}\)
Với \(t = \frac{{6\left( { – \frac{{2\pi }}{3} + k2\pi – 1} \right)}}{\pi };k \in Z\)
Vì \(0 \le t < 24\) nên
\(\begin{array}{l}0 \le \frac{{6\left( { – \frac{{2\pi }}{3} + k2\pi – 1} \right)}}{\pi } \le 24\\ \Leftrightarrow 0 < k \le 2\end{array}\)
Lại do \(k \in Z \Rightarrow k \in \left\{ {1;2} \right\} \Rightarrow t \in \left\{ {\frac{{6\left( { – \frac{{2\pi }}{3} – 1} \right)}}{\pi };\frac{{6\left( {\frac{{4\pi }}{3} – 1} \right)}}{\pi };\frac{{6\left( {\frac{{10\pi }}{3} – 1} \right)}}{\pi }} \right\}\)
Bài 14 trang 41 SGK Toán 11 tập 1 – CD
Đề bài
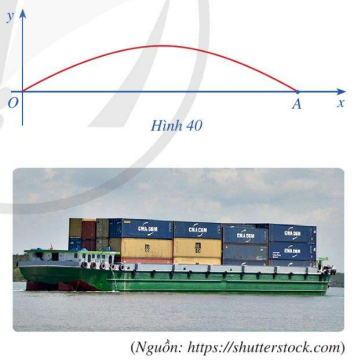
Một cây cầu có dạng cung OA của đồ thị hàm số \(y = 4,8\sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở Hình 40.
a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (Làm tròn kết quả đến hàng phần mười)
b) Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1m.
c) Một sà lan khác cũng chở khối hàng hóa được xếp thành hình hộp chữ nhật với chiều rộng của khối hàng hóa đó là 9m sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều cao của khối hàng hóa đó phải nhỏ hơn 4,3m
Lời giải chi tiết
a) Vì A nằm trên trục Ox nên tung độ của A = 0
Suy ra: $4,8.\sin \frac{x}{9}=0 \Leftrightarrow \sin\frac{x}{9}=0 \Leftrightarrow \frac{x}{9}=\pi \Leftrightarrow x=9\pi $
Vậy chiều rộng của con sông là $9\pi \approx 28,27$ (m)
b) 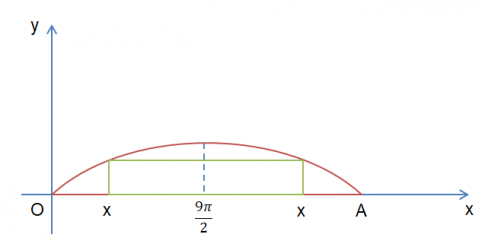
Sà lan có thể đi qua được gầm cầu khi và chỉ khi: $4,8.\sin \frac{x}{9}=3,6 \Leftrightarrow \sin \frac{x}{9}=\frac{3}{4}$
Do $x\in \left [ 0; 9\pi \right ]$ nên $\frac{x}{9}\in \left [ 0;\pi \right ]$
Khi đó: $\frac{x}{9}\approx 0,848 \Rightarrow \frac{x}{9}< 0,85\Rightarrow x< 7,65$
Ta có chiều rộng khối hàng hóa là: $2\left | \frac{9\pi }{2}-x \right |$
Vì $x< 7,65$ nên $2\left | \frac{9\pi }{2}-x \right |< 12,97< 13,1$ (đcpcm)
c) 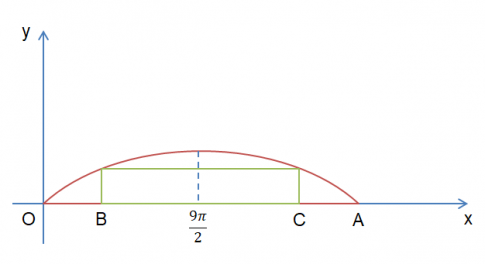
Ta có: BC = 9
Nên $2\left | \frac{9\pi }{2}-x \right |=9 \Rightarrow x=\frac{9}{2}(\pi -1)$
Do đó, chiều cao của khối hàng hóa là: $4,8.sin\left [ \frac{9}{2}(\pi -1).\frac{1}{9} \right ]=4,2< 4,3$ (đcpcm).
