GIẢI SGK Bài tập cuối chương 1 – Toán 11 KNTT – Sách Toán

Đề bài

Trong các khẳng định sau, khẳng định nào là sai?

A. \(\sin \left( {\pi  – \alpha } \right) = \sin \alpha \)

B. \(\cos \left( {\pi  – a} \right) = \cos \alpha \)

C. \(\sin \left( {\pi  + \alpha } \right) =  – \sin \alpha \).

D. \(\cos (\pi  + \alpha ) =  – \cos \alpha \)

Dựa vào liên hệ góc bù nhau và góc hơn kém nhau \(\pi \)

Lời giải chi tiết

Ta có: \(\cos \left( {\pi  – \alpha } \right) =  – \cos \alpha \)

Vậy ta chọn đáp án B

Đề bài

Trong các khẳng định sau, khẳng định nào là sai?

A. \(\cos \left( {a – b} \right) = \cos a\cos b – \sin a\sin b\)

B. \(\sin \left( {a – b} \right) = \sin a\cos b – \cos a\sin b\)

C. \(\cos \left( {a + b} \right) = \cos a\cos b – \sin a\sin b\)

D. \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\)

Dựa vào công thức cộng lượng giác

Lời giải chi tiết

Ta có: \(\cos \left( {a – b} \right) = \cos a\cos b + \sin a\sin b\)

Vậy ta chọn đáp án A

Đề bài

Rút gọn biểu thức \(M = \cos \left( {a + b} \right)\cos \left( {a – b} \right) – \sin \left( {a + b} \right)\sin \left( {a – b} \right)\), ta được

A. \(M = \sin 4a\)

B. \(M = 1 – 2{\cos ^2}a\)

C. \(M = 1 – 2{\sin ^2}a\)

D. \(M = \cos 4a\)

Dựa vào công thức biến đổi tích thành tổng

Lời giải chi tiết

\(\cos \left( {a + b} \right)\cos \left( {a – b} \right) – \sin \left( {a + b} \right)\sin \left( {a – b} \right)\)

\( = \frac{1}{2}\left[ {\cos \left( {a + b – a + b} \right) + \cos \left( {a + b + a – b} \right)} \right] – \frac{1}{2}\left[ {\cos \left( {a + b – a + b} \right) – \cos \left( {a + b + a – b} \right)} \right]\)

\( = \frac{1}{2}\left( {\cos 2b + \cos 2a – \cos 2b + \cos 2a} \right) = \frac{1}{2}.2\cos 2a = \cos 2a = 1 – 2{\sin ^2}a\)

Vậy chọn đáp án C

Đề bài

Khẳng định nào sau đây là sai?

A. Hàm số \(y = \cos x\) có tập xác định là \(\mathbb{R}\)

B. Hàm số \(y = \cos x\) có tập giá trị là [-1;1]

C. Hàm số \(y = \cos x\) là hàm số lẻ

D. Hàm số \(y = \cos x\) tuần hoàn với chu kỳ \(2\pi \)

Dựa vào định nghĩa và tính chất của hàm số \(\cos x\)

Lời giải chi tiết

Ta có: \(y = \cos x\)

\(y\left( { – x} \right) = \cos \left( { – x} \right) = \cos x = y\)

Suy ra hàm số \(y = \cos x\) là hàm số chẵn

Vậy ta chọn đáp án C

Đề bài

Trong các hàm số sau đây, hàm số nào là hàm tuần hoàn?

A. \(y = \tan x + x\)

B. \(y = {x^2} + 1\)

C. \(y = \cot x\)

D. \(y = \frac{{\sin x}}{x}\)

Xét tính tuần hoàn của hàm số

– Xét hàm số \(y = f\left( x \right)\), tập xác định là D

– Với mọi \(x \in D\), ta có \(x – {T_0}\; \in D\) và \(x + {T_0} \in D\;\) Chỉ ra \(f\left( {x + {T_0}} \right) = f\left( x \right)\; = f\left( {x – {T_0}} \right)\)

Vậy hàm số \(y = f\left( x \right)\) tuần hoàn

Lời giải chi tiết

Hàm \(y = \cot x\)là hàm tuần hoàn với chu kì \(T = \pi \)do :

– Tập xác định là \(D = R\backslash \left\{ {k\pi ;k \in Z} \right\}\)

– Với mọi \(x \in D\), ta có \(x – \pi \; \in D\) và \(x + \pi  \in D\;\)

Suy ra

\(\begin{array}{l}f\left( {x + \pi } \right) = \cot \left( {x + \pi } \right) = \cot \left( x \right) = f(x)\\f\left( {x – \pi } \right) = \cot \left( {x – \pi } \right) = \cot \left( x \right) = f\left( x \right)\end{array}\)

Đề bài

Đồ thị của các hàm số \(y = \sin x\) và \(y = \cos x\) cắt nhau tại bao nhiêu điểm có hoành độ thuộc đoạn \(\left[ { – 2\pi ;\frac{{5\pi }}{2}} \right]\)?

A. 5                             B. 6                             C. 4                             D. 7

Dựa vào phương trình hoành độ giao điểm và công thức lượng giác

Lời giải chi tiết

Phương trình hoàn độ giao điểm của hai đồ thì hàm số là \(\sin x = \cos x\)

\( \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Do \(x \in \left[ { – 2\pi ;\frac{{5\pi }}{2}} \right]\; \Leftrightarrow  – 2\pi  \le \frac{\pi }{4} + k\pi  \le \frac{{5\pi }}{2}\;\; \Leftrightarrow \; – \frac{9}{4} \le k \le \frac{9}{4}\;\;\;\)

Mà \(k\; \in \mathbb{Z}\;\; \Leftrightarrow k\; \in \left\{ { – 2;\; – 1;0;1;2} \right\}\)

Vậy ta chọn đáp án A

Đề bài

Tập xác định của hàm số \(y = \frac{{\cos x}}{{\sin x – 1}}\) là

A. \(\mathbb{R}\backslash \{ k2\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)

B. \(\mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k2\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)

C. \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)

D. \(\mathbb{R}\backslash \{ k\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)

adsense

Phân thức xác định khi mẫu thức khác 0

Lời giải chi tiết

Hàm số xác định khi: \(\sin x – 1\; \ne 0\; \Leftrightarrow \sin x \ne 1\; \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi ,\;\;k \in \mathbb{Z}\)

Vậy ta chọn đáp án B

Đề bài

Cho góc \(\alpha \) thỏa mãn \(\frac{\pi }{2} < \alpha  < \pi ,\cos \alpha  =  – \frac{1}{{\sqrt 3 }}\). Tính giá trị của các biểu thức sau:

a) \(\sin \left( {\alpha  + \frac{\pi }{6}} \right)\);

b) \(\cos \left( {\alpha  + \frac{\pi }{6}} \right);\)

c) \(\sin \left( {\alpha  – \frac{\pi }{3}} \right)\);

d) \(\cos \left( {\alpha  – \frac{\pi }{6}} \right)\).

Áp dụng hằng đẳng thức để tính \(\sin \alpha \). Chú ý dấu

Sử dụng công thức cộng lượng giác để tính giá trị biểu thức

Lời giải chi tiết

Ta có:

a) \(\sin \left( {\alpha  + \frac{\pi }{6}} \right) = \sin \alpha \cos \frac{\pi }{6} + \cos \alpha \sin \frac{\pi }{6} = \frac{{\sqrt 6 }}{3}.\frac{{\sqrt 3 }}{2} + \left( { – \frac{1}{{\sqrt 3 }}} \right).\frac{1}{2} = \frac{{ – \sqrt 3  + 3\sqrt 2 }}{6}\)

b) \(\cos \left( {\alpha  + \frac{\pi }{6}} \right) = \cos \alpha .\cos \frac{\pi }{6} – \sin \alpha \sin \frac{\pi }{6} = \left( { – \frac{1}{{\sqrt 3 }}} \right).\frac{{\sqrt 3 }}{2} – \frac{{\sqrt 6 }}{3}.\frac{1}{2} =  – \frac{{3 + \sqrt 6 }}{6}\)

c) \(\sin \left( {\alpha  – \frac{\pi }{3}} \right) = \sin \alpha \cos \frac{\pi }{3} – \cos \alpha \sin \frac{\pi }{3} = \frac{{\sqrt 6 }}{3}.\frac{1}{2} – \left( { – \frac{1}{{\sqrt 3 }}} \right).\frac{{\sqrt 3 }}{2} = \frac{{3 + \sqrt 6 }}{6}\)

d) \(\cos \left( {\alpha  – \frac{\pi }{6}} \right) = \cos \alpha \cos \frac{\pi }{6} + \sin \alpha \sin \frac{\pi }{6} = \left( { – \frac{1}{{\sqrt 3 }}} \right).\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 6 }}{3}.\frac{1}{2} = \frac{{ – 3 + \sqrt 6 }}{6}\)

Đề bài

Cho góc bất kì \(\alpha \). Chứng minh các đẳng thức sau:

a) \({\left( {\sin \alpha  + \cos \alpha } \right)^2} = 1 + \sin 2\alpha ;\;\)

b) \({\cos ^4}\alpha  – {\sin ^4}\alpha  = \cos 2\alpha .\)

Áp dụng hằng đẳng thức đáng nhớ.

Sử dụng công thức nhân đôi để chứng minh

Lời giải chi tiết

a) Ta có: \({\left( {\sin \alpha  + \cos \alpha } \right)^2} = {\sin ^2}\alpha  + 2\sin \alpha \cos \alpha  + {\cos ^2}\alpha  = 1 + \sin 2\alpha \;\)

b) \({\cos ^4}\alpha  – {\sin ^4}\alpha  = \left( {{{\cos }^2}\alpha  – {{\sin }^2}\alpha } \right)\left( {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } \right) = \cos 2\alpha \;\)

Đề bài

Tìm tập giá trị của các hàm số sau:

a) \(y = 2\cos \left( {2x – \frac{\pi }{3}} \right) – 1;\)

b) \(y = \sin x + \cos x\).

Tập giá trị của hàm số là tập min – max của hàm số trên tập xác định

Lời giải chi tiết

a) Tập xác định của hàm số là \(D = \mathbb{R}\)

Vì \( – 1 \le \cos \left( {2x – \frac{\pi }{3}} \right) \le 1 \Leftrightarrow  – 2 \le 2{\rm{cos\;}}\left( {2x – \frac{\pi }{3}} \right) \le 2\;\; \Leftrightarrow  – 3 \le 2\cos \left( {2x – \frac{\pi }{3}} \right) – 1 < 1\)

\( \Rightarrow \) Tập giá trị của hàm số \(y = 2\cos \left( {2x – \frac{\pi }{3}} \right) – 1\) là \(T = \left[ { – 3;1} \right]\).

b) Tập xác định của hàm số là \(D = \mathbb{R}\)

Vì \( – 1 \le \sin x \le 1,\;\; – 1 \le \cos \alpha  \le 1\;\; \Leftrightarrow  – 2 \le \sin x + \cos x \le 2\)

\( \Rightarrow \) Tập giá trị của hàm số \(y = \sin x + \cos x\) là \(T = \left[ { – 2;2} \right]\).

Đề bài

Giải các phương trình sau:

a) \(\cos \left( {3x – \frac{\pi }{4}} \right) =  – \frac{{\sqrt 2 }}{2}\);

b) \(2{\sin ^2}x – 1 + \cos 3x = 0\);

c) \(\tan \left( {2x + \frac{\pi }{5}} \right) = \tan \left( {x – \frac{\pi }{6}} \right)\).

Dựa vào công thức nghiệm tổng quát:

\(\sin x = m\; \Leftrightarrow \sin x = \sin \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha  + k2\pi }\\{x = \pi  – \alpha  + k2\pi }\end{array}\left( {k \in \mathbb{Z}} \right)} \right.\)

\(\cos x = m\;\; \Leftrightarrow \cos x = \cos \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha  + k2\pi }\\{x =  – \alpha  + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)

\(\tan x = m\; \Leftrightarrow \tan x = \tan \alpha  \Leftrightarrow x = \alpha  + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Lời giải chi tiết

a) \(\cos \left( {3x – \frac{\pi }{4}} \right) =  – \frac{{\sqrt 2 }}{2}\;\;\;\; \Leftrightarrow \cos \left( {3x – \frac{\pi }{4}} \right) = \cos \frac{{3\pi }}{4}\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x – \frac{\pi }{4} = \frac{{3\pi }}{4} + k2\pi }\\{3x – \frac{\pi }{4} =  – \frac{{3\pi }}{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \pi  + k2\pi }\\{3x =  – \frac{\pi }{2} + k2\pi }\end{array}} \right.\)

\( \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + \frac{{k2\pi }}{3}}\\{x =  – \frac{\pi }{6} + \frac{{k2\pi }}{3}}\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)

b) \(2{\sin ^2}x – 1 + \cos 3x = 0\;\;\;\;\; \Leftrightarrow \cos 2x + \cos 3x = 0\;\; \Leftrightarrow 2\cos \frac{{5x}}{2}\cos \frac{x}{2} = 0\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos \frac{{5x}}{2} = 0}\\{\cos \frac{x}{2} = 0}\end{array}} \right.\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{{5x}}{2} = \frac{\pi }{2} + k\pi }\\{\frac{{5x}}{2} =  – \frac{\pi }{2} + k\pi }\\{\frac{x}{2} = \frac{\pi }{2} + k\pi }\\{\frac{x}{2} =  – \frac{\pi }{2} + k\pi }\end{array}} \right.\;\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{5} + \frac{{k2\pi }}{5}}\\{x =  – \frac{\pi }{5} + \frac{{k2\pi }}{5}}\\{x = \pi  + k2\pi }\\{x =  – \pi  + k2\pi }\end{array}} \right.\;\;\;\left( {k \in \mathbb{Z}} \right)\)

c) \(\tan \left( {2x + \frac{\pi }{5}} \right) = \tan \left( {x – \frac{\pi }{6}} \right)\;\; \Leftrightarrow 2x + \frac{\pi }{5} = x – \frac{\pi }{6} + k\pi \;\;\; \Leftrightarrow x =  – \frac{{11\pi }}{{30}} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)

Đề bài

Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp của chúng ta được viết là huyết áp tâm thu/huyết áp tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số

                                            \(p\left( t \right) = 115 + 25\sin \left( {160\pi t} \right)\;\)

Trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimet thủy ngân) và thời gian t tính theo phút.

a) Tìm chu kì của hàm số p(t)

b) Tìm số nhịp tim mỗi phút.

c) Tìm chỉ số huyết áp. So sánh huyết áp của người này với huyết áp bình thường.

Chu kỳ \(T = \frac{{2\pi }}{\omega }\)

Hàm số \(y = sin\;x\;\) có tập giá trị là \(\left[ { – 1;1} \right]\)

Giải bất phương trình của hàm số huyết áp

Lời giải chi tiết

a) Chu kỳ của hàm số \(p\left( t \right)\) là \(T = \frac{{2\pi }}{{160\pi }} = \frac{1}{{80}}\)

b) Thời gian giữa hai lần tim đập là \(T = \frac{1}{{80}}\) (phút)

Số nhịp tim mỗi phút là: \(\frac{1}{{\frac{1}{{80}}}} = 80\) (nhịp)

c) Ta có: \( – 1 \le sin\;\left( {160\pi t} \right)\; \le 1,\;\;\forall t \in R\)

\( \Leftrightarrow  – 25 \le 25sin\;\left( {160\pi t} \right)\; \le 25,\;\forall t \in R\;\)

\( \Leftrightarrow 115 – 25 \le 115 + 25sin\;\left( {160\pi t} \right)\; \le 115 + 25,\;\forall t \in R\)

\( \Leftrightarrow 90 \le p\left( t \right) \le 140,\;\forall t \in R\)

Do đó, chỉ số huyết áp của người này là 140/90 và chỉ số huyết áp của người này cao hơn mức bình thường.

Đề bài

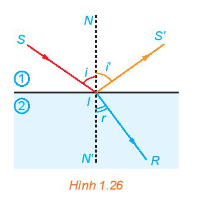
Khi một tia sáng truyền từ không khi vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26. Góc tới i liên hệ với góc khúc xạ r bởi Định luật khúc xạ ánh sáng

                                            \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\)

Ở đây, \({n_1}\) và  \({n_2}\) tương ứng là chiết suất của môi trường 1 (không khí) và môi trường 2 (nước). Cho biết góc tới \(i = {50^0}\), hãy tính góc khúc xạ, biết rằng chiết suất của không khí bằng 1 còn chiết suất của nước là 1,33.

Lời giải chi tiết

Theo bài ra ta có: i = 50°, n1 = 1, n2 = 1,33, thay vào $\frac{sini}{sinr}=\frac{n_{2}}{n_{1}}$ ta được:

$\frac{sin50°}{sinr}=\frac{1.33}{1}$ (điều kiện sin r ≠ 0)

⇒ sin r = $\frac{sin50°}{1.33}$

⇔ sin r ≈ 0,57597 (thỏa mãn điều kiện)

⇔ sin r ≈ sin(35°10’)

⇔ r ≈35°10′ + k360° hoặc r ≈180°-35°10′ + k360° ($k\in Z$)

⇔ r ≈35°10′ + k360° hoặc r ≈144°50′ + k360° ($k\in Z$)

Mà 0° < r < 90° nên r ≈ 35°10’.

Vậy góc khúc xạ r ≈ 35°10’.