adsense
Học Bài 2: Giá trị lượng giác của một góc lượng giác – CTST
============
Lý thuyết
Giá trị lượng giác của một góc lượng giác – SGK Toán 11 Chân trời sáng tạo
1. Giá trị lượng giác của góc lượng giác

– Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\)
– Các giá trị sin\(\alpha \), cos\(\alpha \), tan\(\alpha \), cot\(\alpha \) được gọi là các giá trị lượng giác của góc lượng giác \(\alpha \).
*Chú ý:
a, Trục tung là trục sin, trục hoành là trục côsin.
Trục As có gốc ở điểm A(1;0) và song song với trục sin là trục tang.
Trục Bt có gốc ở điểm B(0;1) và song song với trục coossin gọi là trục côtang.

b, \(\sin \alpha \)và \(\cos \alpha \) xác định với mọi \(\alpha \in \mathbb{R}\).
\(\tan \alpha \)xác định với các góc \(\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
\(\cot \alpha \) xác định với các góc \(\alpha \ne k\pi ,k \in \mathbb{Z}\).
c, Với mọi góc lượng giác \(\alpha \) và số nguyên k, ta có:
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha + k\pi } \right) = \cot \alpha \end{array}\)
d, Bảng các giá trị lượng giác đặc biệt


2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay
– Lần lượt ấn các phím SHIFT \( \to \)MENU \( \to \)2:
Để chọn đơn vị độ: ấn phím 1 (Degree).
Để chọn đơn vị radian: ấn phím 2 (Radian).
– Ấn các phím MENU 1 để vào chế độ tính toán.
3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
-
- Hai góc đối nhau \(\alpha \)và \( – \alpha \)
\(\begin{array}{l}\sin \left( { – \alpha } \right) = – \sin \alpha \\\cos \left( { – \alpha } \right) = \cos \alpha \\\tan \left( { – \alpha } \right) = – \tan \alpha \\\cot \left( { – \alpha } \right) = – \cot \alpha \end{array}\)
-
- Hai góc bù nhau (\(\alpha \)và \(\pi \)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\pi – \alpha } \right) = \sin \alpha \\\cos \left( {\pi – \alpha } \right) = – \cos \alpha \\\tan \left( {\pi – \alpha } \right) = – \tan \alpha \\\cot \left( {\pi – \alpha } \right) = – \cot \alpha \end{array}\)
-
- Hai góc phụ nhau (\(\alpha \)và \(\frac{\pi }{2}\)-\(\alpha \))
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} – \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} – \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} – \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} – \alpha } \right) = \tan \alpha \end{array}\)
-
- Hai góc hơn kém \(\pi \)(và \(\pi \)+\(\alpha \))
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = – \sin \alpha \\\cos \left( {\pi + \alpha } \right) = – \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
Giải mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 – Chân trời sáng tạo
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 1
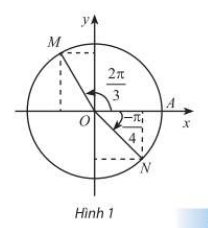
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{\pi }{4}\) trên
đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .
Phương pháp giải:
Dựa vào kiến thức đã học để xác định
Lời giải chi tiết:

Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy
D,E lần lượt là hình chiếu của N lên Ox, Oy
Ta có OM = ON = 1
\(\widehat {MOC} = \frac{{2\pi }}{3} – \frac{\pi }{2} = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {MOC} = \frac{1}{2} = \frac{{MC}}{{OM}} \Rightarrow MC = \frac{1}{2}\\\cos \widehat {MOC} = \frac{{\sqrt 3 }}{2} = \frac{{MB}}{{OM}} \Rightarrow MB = \frac{{\sqrt 3 }}{2}\end{array} \right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M \(\left( {\frac{-1}{2};\frac{{\sqrt 3 }}{2}} \right)\)
\(\widehat {NOD} = – \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {NOD} = – \frac{{\sqrt 2 }}{2} = \frac{{ND}}{{ON}} \Rightarrow ND = – \frac{{\sqrt 2 }}{2}\\\cos \widehat {NOD} = \frac{{\sqrt 2 }}{2} = \frac{{NE}}{{ON}} \Rightarrow NE = \frac{{\sqrt 2 }}{2}\end{array} \right.\)
Tọa độ của điểm N \(\left( { \frac{{\sqrt 2 }}{2};\frac{-{\sqrt 2 }}{2}} \right)\)
Thực hành
Tính \(\sin \left( { – \frac{{2\pi }}{3}} \right)\) và \(\tan 495^\circ \)
Phương pháp giải:
Dựa vào kiến thức đã học ở phần trên để tính
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( { – \frac{{2\pi }}{3}} \right) = – \frac{{\sqrt 3 }}{2}\\\tan 495^\circ = – 1\end{array}\)
Giải mục 2 trang 16 SGK Toán 11 tập 1 – Chân trời sáng tạo
Lựa chọn câu để xem lời giải nhanh hơn
Thực hành 2
Sử dụng máy tính cầm tay để tính
\(\cos 75^\circ \,\,\)và \(\tan \left( { – \frac{{19\pi }}{6}} \right)\)
Phương pháp giải:
Dựa vào kiến thức vừa học được để tính
Lời giải chi tiết:
adsense
\(\begin{array}{l}\cos 75^\circ = \frac{{\sqrt 6 – \sqrt 2 }}{4}\\\tan \left( { – \frac{{19\pi }}{6}} \right) = – \frac{{\sqrt 3 }}{3}\end{array}\)
Giải mục 3 trang 16,17 SGK Toán 11 tập 1 – Chân trời sáng tạo
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 2
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)

b) Chia cả hai vế của biểu thức ở câu a) cho \({\cos ^2}\alpha \) ta được đẳng thức nào?
c) Chia cả hai vế của biểu thức ở câu a) cho \({\sin ^2}\alpha \) ta được đẳng thức nào?
Phương pháp giải:
Dựa vào kiến thức đã học ở phần trên để chứng minh
Lời giải chi tiết:
a) Do \(\begin{array}{l}\sin \alpha = MH \Rightarrow {\sin ^2}\alpha = M{H^2}\\\cos \alpha = OH \Rightarrow {\cos ^2}\alpha = O{H^2}\end{array}\)
Áp dụng định lý Py – Ta – Go vào tam giác OMH vuông tại H ta có:
\(\begin{array}{l}M{H^2} + O{H^2} = O{M^2} = 1\\ \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\end{array}\)
b) Chia cả hai vế cho \({\cos ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\end{array}\)
c) Chia cả hai vế cho \({\sin ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow {\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\end{array}\)
Thực hành 3
Cho \(\tan \alpha = \frac{2}{3}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Tính \(\cos \alpha \) và \(\sin \alpha \)
Phương pháp giải:
Dựa vào công thức đã học ở phần trên để tính
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\\ \Rightarrow {\left( {\frac{2}{3}} \right)^2} + 1 = \frac{1}{{{{\cos }^2}\alpha }}\\ \Rightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{13}}{9}\\ \Rightarrow \cos \alpha = \pm \frac{{3\sqrt {13} }}{{13}}\end{array}\)
Do \(\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \cos \alpha = – \frac{{3\sqrt {13} }}{{13}}\)
Ta có: \(\begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} \Rightarrow \frac{2}{3} = \sin \alpha :\left( { – \frac{{3\sqrt {13} }}{{13}}} \right)\\ \Rightarrow \sin \alpha = – \frac{{2\sqrt {13} }}{{13}}\end{array}\)
Giải mục 4 trang 17, 18 , 19 GK Toán 11 tập 1 – Chân trời sáng tạo
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 3
Cho \(\alpha = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( – \alpha ,\alpha + \pi ,\pi – \alpha ,\frac{\pi }{2} – \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)
Phương pháp giải:
Vẽ đường tròn lượng giác dựa vào kiến thức đã học rồi nhận xét
Lời giải chi tiết:

Dựa vào đường tròn lượng giác ta nhận được:
\(\left. \begin{array}{l}\sin \left( { – \alpha } \right) = – \sin \alpha \\\cos \left( { – \alpha } \right) = \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}tan\left( { – \alpha } \right) = – \tan \alpha \\\cot \left( { – \alpha } \right) = – \cot \alpha \end{array} \right.\)
\(\left. \begin{array}{l}\sin \left( {\pi + \alpha } \right) = – \sin \alpha \\\cos \left( {\pi + \alpha } \right) = – \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array} \right.\)
\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\pi – \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\pi – \frac{\pi }{3}} \right) = – \frac{1}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi – \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\\\cos \left( {\pi – \frac{\pi }{3}} \right) = – \cos \frac{\pi }{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi – \alpha } \right) = \sin \alpha \\\cos \left( {\pi – \alpha } \right) = – \cos \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi – \alpha } \right) = – \tan \alpha \\\cot \left( {\pi – \alpha } \right) = – \cot \alpha \end{array} \right.\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\frac{\pi }{2} – \frac{\pi }{3}} \right) = \frac{1}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\frac{\pi }{2} – \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} – \frac{\pi }{3}} \right) = \cos \frac{\pi }{3}\\\cos \left( {\frac{\pi }{2} – \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} – \alpha } \right) = \cos \alpha \\\cos \left( {\frac{\pi }{2} – \alpha } \right) = \sin \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\frac{\pi }{2} – \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} – \alpha } \right) = \tan \alpha \end{array} \right.\end{array}\)
Thực hành
a) Biểu diễn \(\cos 638^\circ \) qua gí trị lượng giác của góc có số đo từ \(0^\circ \) đến \(45^\circ \)
b) Biểu diễn \(\cot \frac{{19\pi }}{5}\) qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\)
Phương pháp giải:
Dựa vào ví dụ 4 để làm bài
Lời giải chi tiết:
a) \(\cos 638^\circ = \cos \left( {4.180^\circ + 90^\circ – 8^\circ } \right) = – \cos \left( {90^\circ – 8^\circ } \right) = – \sin 8^\circ \)
b) \(\cot \left( {\frac{{19\pi }}{5}} \right) = \cot \left( {4\pi – \frac{\pi }{5}} \right) = – \cot \left( {\frac{\pi }{5}} \right)\)
Vận dụng
Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu với điểm B và C.

a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng \(\left( {13 + 10\sin \alpha } \right)\) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi \(\alpha = – 30^\circ \)
b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải:
Dựa vào kiến thức lượng giác đã học để tính
Lời giải chi tiết:
a) Chiều ca từ điểm B đến mặt đất là độ dài đoạn KH
Ta có: \(KH = OH – OK = 13 – OB.\cos \left( {\frac{\pi }{2} – \alpha } \right) = 13 – 10.\sin \left( { – \alpha } \right) = 13 + 10.\sin \alpha \)
Với \(\alpha = – 30^\circ \Rightarrow KH = 13 + 10.\sin \left( { – 30^\circ } \right) = 8\,\,\left( m \right)\)
b) Nếu B cách mặt đất 4m \( \Rightarrow 4 = 13 + 10\sin \alpha \Leftrightarrow \sin \alpha = – \frac{9}{{10}}\)
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( { – \frac{9}{{10}}} \right)^2} + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = – \frac{{\sqrt {19} }}{{10}}\)
Gọi M là hình chiếu của C lên OH
\( \Rightarrow \cos \left( {\widehat {COH}} \right) = \sin \left( {\frac{\pi }{2} – \alpha } \right) = \cos \alpha = – \frac{{\sqrt {19} }}{{10}}\)
Mà \(\cos \widehat {COH} = \frac{{OM}}{{OC}} \Rightarrow – \frac{{\sqrt {19} }}{{10}} = \frac{{OM}}{{OC}} \Rightarrow OM \approx 4,36\,\,\left( m \right)\)
