adsense
Học Bài 3. Các công thức lượng giác Toán 11 – CTST
=============
Lý thuyết Các công thức lượng giác – SGK Toán 11 CTST
1. Công thức cộng
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a – b} \right) = \sin a\cos b – \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b – \sin asinb\\\cos \left( {a – b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}}\\\tan \left( {a – b} \right) = \frac{{\tan a – \tan b}}{{1 + \tan a\tan b}}\end{array}\)
2. Công thức nhân đôi
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a – {\sin ^2}a = 2{\cos ^2}a – 1 = 1 – 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\end{array}\)
Suy ra, công thức hạ bậc:
\({\sin ^2}a = \frac{{1 – \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
3. Công thức biến đổi tích thành tổng
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a – b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) – \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a – b} \right)} \right]\end{array}\)
4. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\\\cos a – \cos b = – 2\sin \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\\\sin a – \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a – b}}{2}\end{array}\)
Giải hoạt động khởi động trang 20 SGK Toán 11 tập 1 – CTST
Đề bài
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?
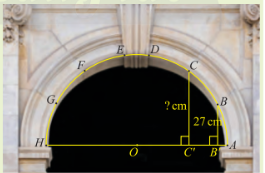
Dựa vào hình vẽ để giải quyết bài toán
Lời giải chi tiết
Đặt chiều rộng cổng AH = d.
\( \Rightarrow OA = OB = \frac{1}{2}d\)
Xét tam giác OBB’ có:
\(\sin \widehat {BOB’} = \frac{{BB’}}{{OB}} = \frac{{27}}{{\frac{d}{2}}} = \frac{{54}}{d}\)
Vì số đo cung AB = số đo cung BC nên số đo cung AC = 2.AB\( \Rightarrow \widehat {AOC} = 2\widehat {BOB’}\)
Xét tam giác OCC’ vuông tại C’ có:
\(\begin{array}{l}\sin \widehat {COC’} = \frac{{CC’}}{{OC}}\\ \Leftrightarrow CC’ = OC.\sin \widehat {COC’} = OC.\sin \left( {2\widehat {BOB’}} \right)\end{array}\)
Mà \(\sin \left( {2\widehat {BOB’}} \right) = 2.\sin \widehat {BOB’}.cos\widehat {BOB’}\)
Vậy để tính khoảng cách từ điểm C đến AH ta phải tìm được \(\sin \widehat {BOB’},cos\widehat {BOB’}\).
Giải mục 1 trang 21 SGK Toán 11 tập 1 – CTST
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 1
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) sau đây:
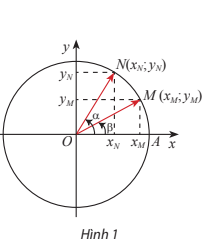
\(\overrightarrow {OM} .\overrightarrow {ON} = \left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {ON} } \right|.cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right)\)\( = cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right) = cos\left( {\alpha – \beta } \right)\)
\(\overrightarrow {OM} .\overrightarrow {ON} = {x_M}.{x_N} + {y_M}.{y_N}\)
Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.
Phương pháp giải:
Dựa vào hình vẽ và 2 công thức tính tích vô hướng để giải quyết
Lời giải chi tiết:
Ta có:
\(cos\left( {\alpha – \beta } \right) = {x_M}.{x_N} + {y_M}.{y_N} = cos\alpha .cos\beta + \sin \alpha .\sin \beta \)
\(cos\left( {\alpha + \beta } \right) = cos\left( {\alpha – \left( { – \beta } \right)} \right) = cos\alpha .cos\left( { – \beta } \right) + \sin \alpha .\sin \left( { – \beta } \right) = cos\alpha .cos\beta – \sin \alpha .\sin \beta \)
Thực hành 1
Tính \(\sin \frac{\pi }{{12}}\) và \(\tan \frac{\pi }{{12}}\)
Phương pháp giải:
Sử dụng công thức \(\sin \left( {a – b} \right) = \sin a\cos b – \cos asinb\).
\(\tan \alpha = \frac{{\sin \alpha }}{{cos\alpha }}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{3} – \frac{\pi }{4}} \right) = \sin \frac{\pi }{3}cos\frac{\pi }{4} – cos\frac{\pi }{3}\sin \frac{\pi }{4}\\ = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} – \frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 6 – \sqrt 2 }}{4}\\{\rm{cos}}\frac{\pi }{{12}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\\\tan \frac{\pi }{{12}} = \frac{{\sin \frac{\pi }{{12}}}}{{{\rm{cos}}\frac{\pi }{{12}}}} = \frac{{\frac{{\sqrt 6 – \sqrt 2 }}{4}}}{{\frac{{\sqrt 6 + \sqrt 2 }}{4}}} = 2 – \sqrt 3 \end{array}\)
Giải mục 2 trang 21, 22 SGK Toán 11 tập 1 – CTST
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 2
Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.
Phương pháp giải:
\(\cos \left( {a + b} \right) = \cos a\cos b – \sin asinb\)
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}}\)
Lời giải chi tiết:
\(\begin{array}{l}\cos \left( {\alpha + \alpha } \right) = \cos 2\alpha = \cos \alpha \cos \alpha – \sin \alpha sin\alpha = {\cos ^2}\alpha – {\sin ^2}\alpha \\ = {\cos ^2}\alpha + {\sin ^2}\alpha – 2{\sin ^2}\alpha = 1 – 2{\sin ^2}\alpha = 2{\cos ^2}a – 1\end{array}\)
\(\tan 2\alpha = \tan \left( {\alpha + \alpha } \right) = \frac{{\tan \alpha + \tan \alpha }}{{1 – \tan \alpha .\tan \alpha }} = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\)
Thực hành 2
Tính \(\cos \frac{\pi }{8}\) và \(\tan \frac{\pi }{8}\)
Phương pháp giải:
Sử dụng công thức
\(\begin{array}{l}\cos 2a = {\cos ^2}a – {\sin ^2}a = 2{\cos ^2}a – 1 = 1 – 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\end{array}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}cos\left( {\frac{\pi }{4}} \right) = cos\left( {2.\frac{\pi }{8}} \right) = 2co{s^2}\frac{\pi }{8} – 1 = \frac{{\sqrt 2 }}{2}\\ \Rightarrow co{s^2}\frac{\pi }{8} = \frac{{\sqrt 2 + 2}}{4}\end{array}\)
adsense
\( \Rightarrow cos\frac{\pi }{8} = \sqrt {\frac{{\sqrt 2 + 2}}{4}} = \frac{{\sqrt {\sqrt 2 + 2} }}{2}\) (vì \(0 < \frac{\pi }{8} < \frac{\pi }{2}\))
Ta có:
\(\tan \left( {\frac{\pi }{4}} \right) = \tan \left( {2.\frac{\pi }{8}} \right) = \frac{{2\tan \frac{\pi }{8}}}{{1 – {{\tan }^2}\frac{\pi }{8}}} = 1\)
\(\begin{array}{l} \Leftrightarrow 1 – {\tan ^2}\frac{\pi }{8} = 2\tan \frac{\pi }{8}\\ \Leftrightarrow {\tan ^2}\frac{\pi }{8} + 2\tan \frac{\pi }{8} – 1 = 0\end{array}\)
\( \Leftrightarrow \tan \frac{\pi }{8} = – 1 + \sqrt 2 \)(vì \(0 < \frac{\pi }{8} < \frac{\pi }{2}\))
Giải mục 3 trang 22 SGK Toán 11 tập 1 – CTST
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 3
Từ công thức cộng, hãy tính tổng và hiệu của:
a) \(\cos \left( {\alpha – b} \right)\) và \(\cos \left( {\alpha + \beta } \right)\);
b) \(\sin \left( {\alpha – \beta } \right)\)và \(\sin \left( {\alpha + \beta } \right)\).
Phương pháp giải:
\(\begin{array}{l}\cos \left( {\alpha – b} \right) = \cos \alpha \cos \beta + \sin \alpha sin\beta \\\cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta – \sin \alpha sin\beta \end{array}\)
\(\begin{array}{l}\sin \left( {\alpha – \beta } \right) = \sin \alpha \cos \beta – \cos \alpha sin\beta \\\sin \left( {\alpha + \beta } \right) = \sin \alpha \cos \beta + \cos \alpha sin\beta \end{array}\)
Lời giải chi tiết:
a,
\(\begin{array}{l}\cos \left( {\alpha – b} \right) + \cos \left( {\alpha + \beta } \right)\\ = \cos \alpha \cos \beta + \sin \alpha sin\beta + \cos \alpha \cos \beta – \sin \alpha sin\beta \\ = 2\cos \alpha \cos \beta \end{array}\)
\(\begin{array}{l}\cos \left( {\alpha – b} \right) – \cos \left( {\alpha + \beta } \right)\\ = \cos \alpha \cos \beta + \sin \alpha sin\beta – \cos \alpha \cos \beta + \sin \alpha sin\beta \\ = 2\sin \alpha sin\beta \end{array}\)
b,
\(\begin{array}{l}\sin \left( {\alpha – \beta } \right) – \sin \left( {\alpha + \beta } \right)\\ = \sin \alpha \cos \beta – \cos \alpha sin\beta – \sin \alpha \cos \beta – \cos \alpha sin\beta \\ = – 2\cos \alpha sin\beta \end{array}\)
\(\begin{array}{l}\sin \left( {\alpha – \beta } \right) + \sin \left( {\alpha + \beta } \right)\\ = \sin \alpha \cos \beta – \cos \alpha sin\beta + \sin \alpha \cos \beta + \cos \alpha sin\beta \\ = 2\sin \alpha \cos \beta \end{array}\)
Thực hành 3
Tính giá trị của các biểu thức\(\sin \frac{\pi }{{24}}\cos \frac{{5\pi }}{{24}}\) và \(\sin \frac{{7\pi }}{8}\sin \frac{{5\pi }}{8}\)
Phương pháp giải:
Áp dụng công thức
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a – b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) – \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a – b} \right)} \right]\end{array}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\sin \frac{\pi }{{24}}\cos \frac{{5\pi }}{{24}} = \frac{1}{2}\left[ {\sin \left( {\frac{\pi }{{24}} + \frac{{5\pi }}{{24}}} \right) + \sin \left( {\frac{\pi }{{24}} – \frac{{5\pi }}{{24}}} \right)} \right]\\ = \frac{1}{2}\left[ {\sin \left( {\frac{\pi }{4}} \right) + \sin \left( { – \frac{\pi }{6}} \right)} \right]\\ = \frac{1}{2}\left[ {\frac{{\sqrt 2 }}{2} – \frac{1}{2}} \right] = \frac{{\sqrt 2 – 1}}{4}\end{array}\)
Ta có:
\(\begin{array}{l}\sin \frac{{7\pi }}{8}\sin \frac{{5\pi }}{8} = \frac{1}{2}\left[ {\cos \left( {\frac{{7\pi }}{8} – \frac{{5\pi }}{8}} \right) – \cos \left( {\frac{{7\pi }}{8} + \frac{{5\pi }}{8}} \right)} \right]\\ = \frac{1}{2}\left[ {\cos \left( {\frac{\pi }{4}} \right) – \cos \left( {\frac{{3\pi }}{2}} \right)} \right]\\ = \frac{1}{2}.\left( {\frac{{\sqrt 2 }}{2} + 0} \right) = \frac{{\sqrt 2 }}{4}\end{array}\)
Giải mục 4 trang 22, 23 SGK Toán 11 tập 1 – CTST
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động 4
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác \(\alpha = \frac{{\alpha + \beta }}{2},\beta = \frac{{\alpha – \beta }}{2}\) ta được đẳng thức nào?
Phương pháp giải:
Áp dụng công thức
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a – b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) – \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a – b} \right)} \right]\end{array}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha – \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} – \frac{{\alpha – \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha – \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} – \frac{{\alpha – \beta }}{2}} \right) – \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha – \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta – \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha – \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha – \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} – \frac{{\alpha – \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)
Thực hành 4
Tính \(\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}}\)
Phương pháp giải:
Áp dụng công thức
\(\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a – b}}{2}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}} = 2\cos \frac{{\frac{{7\pi }}{{12}} + \frac{\pi }{{12}}}}{2}\cos \frac{{\frac{{7\pi }}{{12}} – \frac{\pi }{{12}}}}{2}\\ = 2.\frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{2}\end{array}\)
Vận dụng
Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính \(\sin \alpha \) và \(\cos \alpha \), từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.
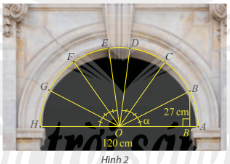
Phương pháp giải:
Quan sát hình vẽ để trả lời.
Lời giải chi tiết:
Ta có: \(OA = OB = 120:2 = 60\)
Xét tam giác OBB’ có:
\(\sin \widehat {BOB’} = \frac{{BB’}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}\)
\(\widehat {AOC} = 2\widehat {BOB’}\)
(Vì số đo cung AC gấp 2 lần số đo cung AB)
Xét tam giác OCC’ vuông tại C’ có:
\(\begin{array}{l}\sin \widehat {COC’} = \frac{{CC’}}{{OC}}\\ \Leftrightarrow CC’ = OC.\sin \widehat {COC’} = OC.\sin \left( {2\widehat {BOB’}} \right)\end{array}\)
Mà \(\sin \left( {2\widehat {BOB’}} \right) = 2.\sin \widehat {BOB’}.cos\widehat {BOB’}\)
\( = 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}\)
Vậy khoảng cách từ C đến AH là \(60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm\).
