Học Bài 4. Hàm số lượng giác và đồ thị – Toán 11 CTST – Sách Toán

1. Hàm số lượng giác

• • Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là \(\mathbb{R}\).

 

• • Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là \(\mathbb{R}\).

 

• • Hàm số cho bằng công thức \(y = \frac{{\sin \alpha }}{{\cos \alpha }}\)được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).

 

• • Hàm số cho bằng công thức \(y = \frac{{\cos \alpha }}{{\sin \alpha }}\) được gọi là hàm số côtang, kí hiệu là y = cotx. Tập xác định của hàm số côtang là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).

 

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a, Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) có tập xác định là D.

Hàm số f(x) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( – x \in D\) và \(f( – x) = f(x)\). Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.

Hàm số f(x) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( – x \in D\) và \(f( – x) =  – f(x)\). Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

     b, Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T \( \ne \) 0 sao cho với mọi \(x \in D\) ta có \(x \pm T \in D\) và \(f(x + T) = f(x)\)

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2\(\pi \).

Các hàm số y = tanx, y=cotx tuần hoàn chu kì \(\pi \).

3. Đồ thị của các hàm số lượng giác

 a, Hàm số y =  sinx

• • Tập xác định là \(\mathbb{R}\).

 

• • Tập giá trị là [-1;1].

 

• • Là hàm số lẻ và tuần hoàn chu kì 2\(\pi \).

 

• • Đồng biến trên mỗi khoảng \(\left( { – \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).

 

• • Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

 

b, Hàm số y =  cosx

• • Tập xác định là \(\mathbb{R}\).

 

• • Tập giá trị là [-1;1].

 

• • Là hàm số chẵn và tuần hoàn chu kì 2\(\pi \).

 

• • Đồng biến trên mỗi khoảng \(\left( { – \pi  + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi  + k2\pi } \right)\).

 

• • Có đồ thị là một đường hình sin đối xứng qua trục tung.

 

c, Hàm số y =  tanx

• • Tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).

 

• • Tập giá trị là \(\mathbb{R}\).

 

• • Là hàm số lẻ và tuần hoàn chu kì \(\pi \).

 

• • Đồng biến trên mỗi khoảng \(\left( { – \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\), \(k \in \mathbb{Z}\).

 

• • Có đồ thị đối xứng qua gốc tọa độ.

 

d, Hàm số y =  cotx

• • Tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).

 

• • Tập giá trị là \(\mathbb{R}\).

 

• • Là hàm số lẻ và tuần hoàn chu kì \(\pi \).

 

• • Đồng biến trên mỗi khoảng \(\left( {k\pi ;\pi  + k\pi } \right)\), \(k \in \mathbb{Z}\).

 

• • Có đồ thị đối xứng qua gốc tọa độ.

 

 

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 1

Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác. Sử dụng định nghĩa của các giá trị lượng giác, hãy giải thích vì sao xác định duy nhất:

a) Giá trị sint và cost

b) Giá trị tant (nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)) và \(\cot t\)(nếu \(t \ne k\pi ,k \in \mathbb{Z}\)).

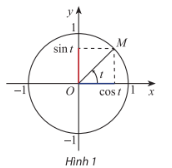
Phương pháp giải:

Quan sát hình vẽ để trả lời.

Lời giải chi tiết:

a) Ta thấy \(\sin t = {y_M}\) là tung độ của điểm M trên đường tròn lượng giác và c\(\cos t = {x_M}\) là hoành độ của điểm M trên đường tròn lượng giác.

Với mỗi điểm M xác định, ta chỉ có 1 tung độ và hoành độ duy nhất

Nên ta chỉ xác định duy nhất giá trị sint và cost.

b,

Nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\), ta có: \(\tan t = \frac{{\sin t}}{{{\rm{cost}}}} = \frac{{{y_M}}}{{{x_M}}}\)( \({x_M} \ne 0\))

Nếu \(t \ne k\pi ,k \in \mathbb{Z}\), ta có: \(\cot t = \frac{{{\rm{cost}}}}{{{\rm{sint}}}} = \frac{{{x_M}}}{{{y_M}}}\)( \({y_M} \ne 0\))

Do \({x_M}\), \({y_M}\)xác định duy nhất nên \(\tan t\), \(\cot t\)xác định duy nhất.

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 2

Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.

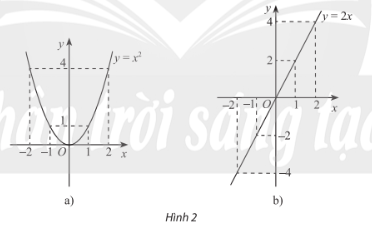
Phương pháp giải:

Quan sát đồ thị để trả lời.

Lời giải chi tiết:

* Hàm số \(y = {x^2}\)

Nhìn đồ thị ta thấy:

+ \(y(1) = y( – 1) = 1,y(2) = y( – 2) = 4\)

+ Đồ thị hàm số đối xứng qua trục Oy.

* Hàm số \(y = 2x\)

Nhìn đồ thị ta thấy:

+ \(y(1) =  – y( – 1),y(2) =  – y( – 2)\)

+ Đồ thị hàm số đối xứng qua điểm O.

Thực hành 1

Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ.

Phương pháp giải:

Cho hàm số y = f(x) có tập xác định là D. Hàm số f(x) được gọi là hàm số lẻ nếu \(\forall x \in D\)thì \( – x \in D\)và \(f( – x) =  – f(x)\).

Lời giải chi tiết:

* Hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}}\)

Tập xác định \({\rm{D}} = \mathbb{R}\).

Với mọi \(x \in \mathbb{R}\)thì \( – x \in \mathbb{R}\) và \({\mathop{\rm s}\nolimits} {\rm{in}}\left( { – x} \right) =  – {\mathop{\rm s}\nolimits} {\rm{in}}x\).

Vậy nên \(y = {\mathop{\rm s}\nolimits} {\rm{inx}}\) là hàm số lẻ.

* Hàm số \(y = \cot x\)

Tập xác định \({\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).

Với mọi \(x \in \mathbb{R}\)thì \( – x \in \mathbb{R}\) và \(\cot \left( { – x} \right) =  – \cot x\).

Vậy nên \(y = \cot {\rm{x}}\) là hàm số lẻ.

Hoạt động 3

Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi \(x \in \mathbb{R}\).

Phương pháp giải:

Dựa vào tính chất

\(\begin{array}{l}\sin \left( {\alpha  + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha  + k2\pi } \right) = \cos \alpha \\\tan \left( {\alpha  + k\pi } \right) = \tan \alpha \\\cot \left( {\alpha  + k\pi } \right) = \cot \alpha \end{array}\)

Lời giải chi tiết:

Do \(\sin \left( {x + k2\pi } \right) = \sin x\),\(k \in \mathbb{Z}\).

\( \Rightarrow \sin \left( {x + 2\pi } \right) = \sin x\)

Nên \(T = 2\pi \).

Thực hành 2

Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx

Phương pháp giải:

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T \( \ne \)0 sao cho với mọi \(x \in D\)ta có \(x \pm T \in D\) và\(f(x + T) = f(x)\)

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

Lời giải chi tiết:

* Hàm số y = cosx

+ Tập xác định \({\rm{D}} = \mathbb{R}\).

+ Với mọi \(x \in \mathbb{R}\)ta có \(x \pm 2\pi  \in D\) và\(\cos (x + 2\pi ) = \cos (x)\)

Vậy hàm số y = cosx là hàm tuần hoàn vỡi chu kì \(T = 2\pi \).

* Hàm số y = cotx

+ Tập xác định \({\rm{D}} = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\).

+ Với mọi \(x \in \mathbb{R}\)ta có \(x \pm \pi  \in D\) và\(\cot (x + \pi ) = \cot (x)\)

Vậy hàm số y = cosx là hàm tuần hoàn vỡi chu kì \(T = \pi \).