Học Bài 4. Phương trình lượng giác cơ bản – Toán 11 KNTT – Sách Toán

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 1

Cho hai phương trình \(2x – 4 = 0\) và \(\left( {x – 2} \right)\left( {{x^2} + 1} \right) = 0\).

Tìm và so sánh tập nghiệm của hai phương trình trên

Phương pháp giải:

Giải phương trình và so sánh tập nghiệm của 2 phương trình

Lời giải chi tiết:

Ta có:

Tập nghiệm của phương trình là \({S_1} = \left\{ 2 \right\}\)

\(\left( {x – 2} \right)\left( {{x^2} + 1} \right) = 0\; \Leftrightarrow x – 2 = 0\; \Leftrightarrow x = 2\)

Tập nghiệm của phương trình là \({S_2} = \left\{ 2 \right\}\)

Vậy tập nghiệm của 2 phương trình là tương đương.

Luyện tập 1

Xét sự tương đương của hai phương trình sau:

\(\frac{{x – 1}}{{x + 1}} = 0\) và \({x^2} – 1 = 0\)

Phương pháp giải:

Giải nghiệm của 2 phương trình và so sánh tập nghiệm.

Lưu ý điều kiện xác định của phương trình

Lời giải chi tiết:

Ta có: \(\frac{{x – 1}}{{x + 1}}\;\)xác định khi \(x + 1 \ne 0 \Leftrightarrow x \ne  – 1\)

\(\frac{{x – 1}}{{x + 1}} = 0 \Leftrightarrow x – 1 = 0 \Leftrightarrow x = 1\;\)

Tập nghiệm của phương trình là \({S_1} = \left\{ 1 \right\}\)

\({x^2} – 1 = 0 \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x =  – 1}\end{array}} \right.\;\)

Tập nghiệm của phương trình là \({S_2} = \left\{ {1; – 1} \right\}\)

Vậy tập nghiệm của 2 phương trình là không tương đương nhau

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 2

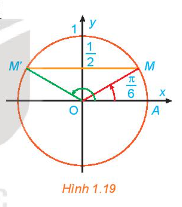
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ {0;2\pi } \right]\)

b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Phương pháp giải:

Nghiệm của phương trình \(\sin x = \frac{1}{2}\) là hoành độ các giao điểm của đường thẳng \(y = \frac{1}{2}\) và đồ thị hàm số \(y = \sin x\)

Lời giải chi tiết:

a) Từ Hình 1.19, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, – \frac{{5\pi }}{6}\)

b) Vì hàm số \(\sin x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi  – \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)

Luyện tập

Giải các phương trình sau: a) \(\sin x = \frac{{\sqrt 2 }}{2}\);        b) \(\sin 3x =  – \sin 5x\)

Phương pháp giải:

Dựa vào công thức nghiệm tổng quát:

\(\sin x = m\; \Leftrightarrow \sin x = \sin \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha  + k2\pi }\\{x = \pi  – \alpha  + k2\pi }\end{array}\left( {k \in \mathbb{Z}} \right)} \right.\)

Áp dụng công thức cộng lượng giác

Lời giải chi tiết:

a) \(\sin x = \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \sin x = \sin \frac{\pi }{4}\;\;\;\; \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi  – \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)

b)

\(\begin{array}{l}\sin 3x =  – \sin 5x\;\;\;\\\; \Leftrightarrow \,\,\,\sin 3x + \sin 5x = 0\;\;\;\;\;\;\\ \Leftrightarrow \,\,\,2\sin 4x\cos x = 0\;\end{array}\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = 0}\\{\cos x = 0}\end{array}\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = \sin 0}\\{\cos x = \cos \frac{\pi }{2}}\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = k\pi }\\{x = \frac{\pi }{2} + k\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.} \right.\)

Lựa chọn câu để xem lời giải nhanh hơn

adsense

Hoạt động 3

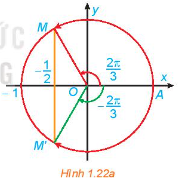
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ { – \pi ;\pi } \right)\).

b) Dựa vào tính tuần hoản của hàm số cosin, hãy viết công thức nghiệm của phương trình đã cho.

Phương pháp giải:

Nghiệm của phương trình \(\cos x =  – \frac{1}{2}\) là hoành độ các giao điểm của đường thẳng \(y =  – \;\frac{1}{2}\) và đồ thị hàm số \(y = \cos x\)

Lời giải chi tiết:

a) Từ Hình 1.20, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, – \frac{{5\pi }}{6}\)

b) Vì hàm số \(\cos x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi  – \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)

Luyện tập 3

Giải các phương trình sau: a) \(2\cos x =  – \sqrt 2 \);            b) \(\cos 3x – \sin 5x = 0\)

Phương pháp giải:

Dựa vào công thức nghiệm tổng quát:

\(\cos x = m\;\; \Leftrightarrow \cos x = \cos \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha  + k2\pi }\\{x =  – \alpha  + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)

Lời giải chi tiết:

a) \(2\cos x =  – \sqrt 2  \Leftrightarrow \cos x =  – \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \cos x = \cos \frac{\pi }{4} \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi  – \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)

b) \(\cos 3x – \sin 5x = 0\;\;\;\; \Leftrightarrow \cos 3x = \sin 5x\;\;\;\; \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} – 5x} \right)\;\;\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \frac{\pi }{2} – 5x + k2\pi }\\{3x =  – \frac{\pi }{2} + 5x + k2\pi }\end{array}} \right.\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{8x = \frac{\pi }{2} + k2\pi }\\{ – 2x =  – \frac{\pi }{2} + k2\pi }\end{array}} \right.\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{\pi }{4} – k\pi }\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)

vận dụng 1

Khi mặt trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là \(\alpha \left( {{0^0} \le \;\alpha  \le {{360}^0}} \right)\)thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bới công thức:

\(F = \frac{1}{2}\left( {1 – \cos \alpha } \right)\).

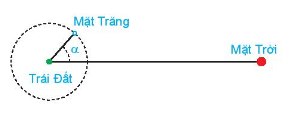
Xác định góc \(\alpha \) tương ứng với các pha sau của Mặt Trăng.

a) \(F = 0\) (trăng mới)

b) \(F = 0,25\) (trăng lưỡi liềm)

c) \(F = 0,5\) (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng)

d) \(F = 1\) (trăng tròn)

Phương pháp giải:

Thay giá trị F tương ứng rồi giải phương trình để tìm \(\alpha \)

Lời giải chi tiết:

a)

\(\begin{array}{l}F = 0\;\\ \Rightarrow \frac{1}{2}\left( {1 – \cos \alpha } \right) = 0\;\; \Leftrightarrow 1 – \cos \alpha  = 0\;\; \Leftrightarrow \cos \alpha  = 1\; \Leftrightarrow \alpha  = k2\pi \;\left( {k \in \mathbb{Z}} \right)\end{array}\)

b) \(F = 0,25\; \Rightarrow \frac{1}{2}\left( {1 – \cos \alpha } \right) = 0,25\; \Leftrightarrow 1 – \cos \alpha  = \frac{1}{2}\;\; \Leftrightarrow \cos \alpha  = \frac{1}{2}\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha  = \frac{\pi }{3} + k2\pi }\\{\alpha  =  – \frac{\pi }{3} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)

c) \(F = 0,5\;\; \Rightarrow \frac{1}{2}\left( {1 – \cos \alpha } \right) = 0,5\; \Leftrightarrow 1 – \cos \alpha  = 1\; \Leftrightarrow \cos \alpha  = 0\; \Leftrightarrow \alpha  = \frac{\pi }{2} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)

d) \(F = 1\; \Leftrightarrow \frac{1}{2}\left( {1 – \cos \alpha } \right) = 1\;\; \Leftrightarrow 1 – \cos \alpha  = 2\; \Leftrightarrow \cos \alpha  =  – 1\; \Leftrightarrow \alpha  = \pi  + k2\pi \;\left( {k \in \mathbb{Z}} \right)\)

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 4

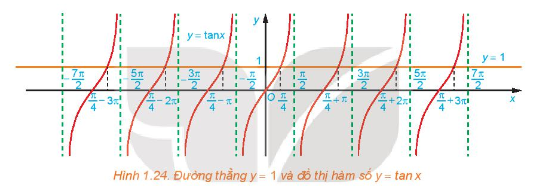
a) Quan sát Hình 1.24, hãy cho biết đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\) tại mấy điểm trên khoảng \(\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)?\)

b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho

Phương pháp giải:

Nghiệm của phương trình \(\tan x = 1\) là hoành độ các giao điểm của đường thẳng \(y = 1\) và đồ thị hàm số \(y = \tan x\)

Lời giải chi tiết:

a) Từ Hình 1.24, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\;\)tại 1 điểm \(x = \frac{\pi }{4}\) trên khoảng \(\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)\)

b) Ta có công thức nghiệm của phương trình là: \(x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Luyện tập 4

Giải các phương trình sau:

a) \(\sqrt 3 \tan 2x =  – 1\);                              b) \(\tan 3x + \tan 5x = 0\)’

Phương pháp giải:

Dựa vào công thức nghiệm tổng quát: \(\tan x = m\; \Leftrightarrow \tan x = \tan \alpha  \Leftrightarrow x = \alpha  + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Lời giải chi tiết:

a) \(\sqrt 3 \tan 2x =  – 1\;\; \Leftrightarrow \tan 2x =  – \frac{1}{{\sqrt 3 }}\;\;\; \Leftrightarrow \tan 2x = \tan  – \frac{\pi }{6}\; \Leftrightarrow 2x =  – \frac{\pi }{6} + k\pi \)

\(\;\; \Leftrightarrow x =  – \frac{\pi }{{12}} + \frac{{k\pi }}{2}\;\left( {k \in \mathbb{Z}} \right)\)

b) \(\tan 3x + \tan 5x = 0\;\; \Leftrightarrow \tan 3x = \tan \left( { – 5x} \right) \Leftrightarrow 3x =  – 5x + k\pi \;\; \Leftrightarrow 8x = k\pi \;\; \Leftrightarrow x = \frac{{k\pi }}{8}\;\left( {k \in \mathbb{Z}} \right)\)

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 5

a) Quan sát Hình 1.25, hãy cho biết đường thẳng \(y =  – 1\) cắt đồ thị hàm số \(y = \cot x\) tại mấy điểm trên khoảng \(\left( {0;\pi } \right)?\)

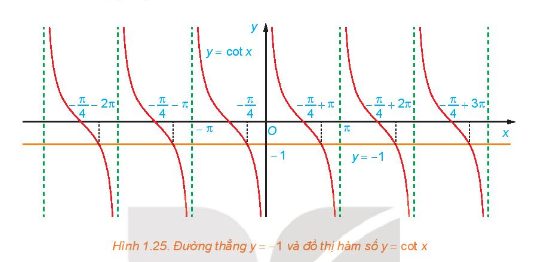
b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.

Phương pháp giải:

Nghiệm của phương trình \(\cot x =  – 1\) là hoành độ các giao điểm của đường thẳng \(y =  – 1\) và đồ thị hàm số \(y = \cot x\)

Lời giải chi tiết:

a) Từ Hình 1.25, ta thấy đường thẳng \(y =  – 1\) cắt đồ thị hàm số \(y = \cot x\;\)tại 1 điểm \(x =  – \frac{\pi }{4} + \pi \) trên khoảng \(\left( {0;\pi } \right)\)

b) Ta có công thức nghiệm của phương trình là: \(x =  – \frac{\pi }{4} + \pi  + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Luyện tập

Giải các phương trình sau:

a) \(\cot x = 1;\)                                                           b) \(\sqrt 3 \cot x + 1 = 0\)

Phương pháp giải:

Sử dụng công thức nghiệm  \(\cot x = m\; \Leftrightarrow \cot x = \cot \alpha  \Leftrightarrow x = \alpha  + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)

Lời giải chi tiết:

a) \(\cot x = 1\; \Leftrightarrow \cot x = \cot \frac{\pi }{4}\;\;\; \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

b) \(\sqrt 3 \cot x + 1 = 0\;\;\; \Leftrightarrow \sqrt 3 \cot x =  – 1\; \Leftrightarrow \cot x =  – \frac{{\sqrt 3 }}{3}\;\; \Leftrightarrow \cot x = \cot \left( { – \frac{\pi }{3}} \right)\)

\( \Leftrightarrow x =  – \frac{\pi }{3} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Đề bài

Sử dụng máy tính cầm tay, tìm số đo độ và radian của góc \(\alpha \), biết:

a) \(\cos \alpha  =  – 0,75\)

b) \(\tan \alpha  = 2,46\)

c) \(\cot \alpha  =  – 6,18\)

Bấm Shift + sin/cos/tan để tìm số đo độ và radian. Chú ý đổi về độ và radian

Lời giải chi tiết

a) \(\cos \alpha  =  – 0,75\)

\( \Leftrightarrow \alpha  ={138^ \circ }35’36”\) hay \(\alpha  =2,4188584\)

b) \(\tan \alpha  =  2,46\)

\( \Leftrightarrow \alpha  ={67^ \circ }52’01”\) hay \(\alpha  =1,1846956\)

c) \(\cos \alpha  =  -6,18\)

\( \Leftrightarrow \alpha  ={170^ \circ }48’62”\) hay \(\alpha  =2,98117\)