I. Định nghĩa khoảng cách từ điểm đến đường thẳng
– Khoảng cách từ điểm (M) đến đường thẳng (Delta ) là khoảng cách giữa hai điểm (M) và (H), trong đó (H) là hình chiếu của điểm (M) trên đường thẳng (Delta ).
Kí hiệu: (dleft( {M,Delta } right) = MH) trong đó (H) là hình chiếu của (M) trên (Delta ).
II. Bài toán tính khoảng cách từ một điểm đến một đường thẳng
Phương pháp:
Để tính khoảng cách từ điểm $M$ đến đường thẳng $Delta $ ta cần xác định được hình chiếu $H$ của điểm $M$ trên đường thẳng $Delta $, rồi xem $MH$ là đường cao của một tam giác nào đó để tính.
Điểm $H$ thường được dựng theo hai cách sau:
Cách 1: Trong $mpleft( {M,Delta } right)$ vẽ $MH bot Delta Rightarrow dleft( {M,Delta } right) = MH$
Cách 2: Dựng mặt phẳng $left( alpha right)$ qua $M$ và vuông góc với $Delta $ tại $H$.
Khi đó $dleft( {M,Delta } right) = MH$.
Hai công thức sau thường được dùng để tính $MH$
CT1: $Delta MAB$ vuông tại $M$ và có đường cao $MH$ thì $dfrac{1}{{M{H^2}}} = dfrac{1}{{M{A^2}}} + dfrac{1}{{M{B^2}}}$.
CT2: $MH$ là đường cao của $Delta MAB$ thì $MH = dfrac{{2{S_{MAB}}}}{{AB}}$.
Ví dụ: Cho hình chóp tam giác $S.ABC$ với $SA$ vuông góc với $left( {ABC} right)$ và $SA{rm{ }} = {rm{ }}3a.$ Diện tích tam giác $ABC$ bằng (2{a^2},BC = a). Khoảng cách từ $S$ đến $BC$ bằng bao nhiêu?
A. (2a.) B. $4a.$
C. $3a.$ D. $5a.$
Hướng dẫn giải:
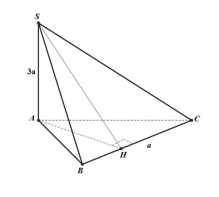
Kẻ $AH$ vuông góc với $BC:$ ({S_{Delta ABC}} = dfrac{1}{2}AH.BC Rightarrow AH = dfrac{{2.{S_{Delta ABC}}}}{{BC}} = dfrac{{4{a^2}}}{a} = 4a)
Ta có: (SA bot left( {ABC} right) Rightarrow SA bot BC)
Lại có (AH bot BC) nên (BC bot left( {SAH} right) Rightarrow BC bot SH)
Do đó khoảng cách từ $S$ đến $BC$ chính là $SH.$
Dựa vào tam giác vuông (Delta SAH) ta có (SH = sqrt {S{A^2} + A{H^2}} = sqrt {{{(3a)}^2} + {{(4a)}^2}} = 5a)
