I. Các định nghĩa và tính chất về khoảng cách giữa hai đường thẳng chéo nhau
– Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó.
Kí hiệu: (dleft( {a,b} right) = MN) trong đó (M in a,N in b) và (MN bot a,MN bot b).
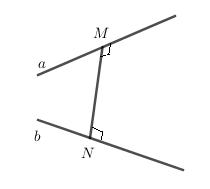
+) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó mà chứa đường thẳng còn lại.
+) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
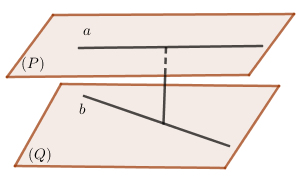
Kí hiệu: (dleft( {a,b} right) = dleft( {a,left( Q right)} right) = dleft( {b,left( P right)} right) = dleft( {left( P right),left( Q right)} right)) trong đó (left( P right),left( Q right)) hai mặt phẳng lần lượt chứa các đường thẳng (a,b) và (left( P right)//left( Q right))
II. Phương pháp tính khoảng cách giữa hai đường thẳng
Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau:
+) Phương pháp 1: Dựng đoạn vuông góc chung $MN$ của $a$ và $b$, khi đó $dleft( {a,b} right) = MN$.
Một số trường hợp hay gặp khi dựng đoạn vuông góc chung của hai đường thẳng chéo nhau:
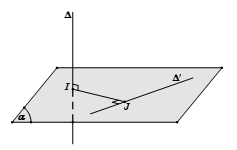
Trường hợp 1: $Delta $ và $Delta ‘$ vừa chéo nhau vừa vuông góc với nhau
– Bước 1: Chọn mặt phẳng $(alpha )$ chứa $Delta ‘$ và vuông góc với $Delta $ tại $I$.
– Bước 2: Trong mặt phẳng $(alpha )$ kẻ $IJ bot Delta ‘$.
Khi đó $IJ$ là đoạn vuông góc chung và $d(Delta ,Delta ‘) = IJ$.
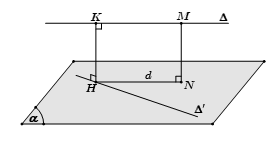
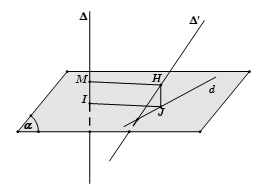
Trường hợp 2: $Delta $ và $Delta ‘$ chéo nhau mà không vuông góc với nhau
– Bước 1: Chọn mặt phẳng $(alpha )$ chứa $Delta ‘$ và song song với $Delta $.
– Bước 2: Dựng $d$ là hình chiếu vuông góc của $Delta $ xuống $(alpha )$ bằng cách lấy điểm $M in Delta $ dựng đoạn $MN bot left( alpha right)$, lúc đó $d$ là đường thẳng đi qua $N$ và song song với $Delta $.
– Bước 3: Gọi $H = d cap Delta ‘$, dựng $HK//MN$
Khi đó $HK$ là đoạn vuông góc chung và $d(Delta ,Delta ‘) = HK = MN$.
Hoặc
– Bước 1: Chọn mặt phẳng $(alpha ) bot Delta $ tại $I$.
– Bước 2: Tìm hình chiếu $d$ của $Delta ‘$ xuống mặt phẳng $(alpha )$.
– Bước 3: Trong mặt phẳng $(alpha )$, dựng $IJ bot d$, từ $J$ dựng đường thẳng song song với $Delta $ cắt $Delta ‘$ tại $H$, từ $H$ dựng $HM//IJ$.
Khi đó $HM$ là đoạn vuông góc chung và $d(Delta ,Delta ‘) = HM = IJ$.
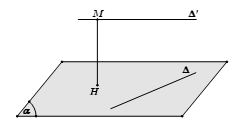
+) Phương pháp 2: Chọn mặt phẳng $(alpha )$ chứa đường thẳng $Delta $ và song song với $Delta ‘$. Khi đó $d(Delta ,Delta ‘) = d(Delta ‘,(alpha ))$
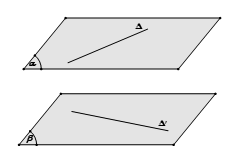
+) Phương pháp 3: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.
+) Phương pháp 4: Sử dụng phương pháp vec tơ
a) $MN$ là đoạn vuông góc chung của $AB$ và $CD$ khi và chỉ khi $left{ begin{array}{l}overrightarrow {AM} = xoverrightarrow {AB} \overrightarrow {CN} = yoverrightarrow {CD} \overrightarrow {MN} .overrightarrow {AB} = 0\overrightarrow {MN} .overrightarrow {CD} = 0end{array} right.$
b) Nếu trong $left( alpha right)$ có hai vec tơ không cùng phương $overrightarrow {{u_1}} ,overrightarrow {{u_2}} $ thì $OH = dleft( {O,left( alpha right)} right) Leftrightarrow left{ begin{array}{l}overrightarrow {OH} bot overrightarrow {{u_1}} \overrightarrow {OH} bot overrightarrow {{u_2}} \H in left( alpha right)end{array} right. Leftrightarrow left{ begin{array}{l}overrightarrow {OH} .overrightarrow {{u_1}} = 0\overrightarrow {OH} .overrightarrow {{u_2}} = 0\H in left( alpha right)end{array} right.$
