I. Vị trí tương đối giữa hai đường thẳng
Cho (d,d’) là các đường thẳng có VTCP lần lượt là (overrightarrow u ,overrightarrow {u’} ,M in d,M’ in d’) . Ta có:
+) (d equiv d’ Leftrightarrow overrightarrow u ,overrightarrow {u’} ,overrightarrow {MM’} ) đôi một cùng phương ( Leftrightarrow left[ {overrightarrow u ,overrightarrow {u’} } right] = left[ {overrightarrow u ,overrightarrow {MM’} } right] = overrightarrow 0 )
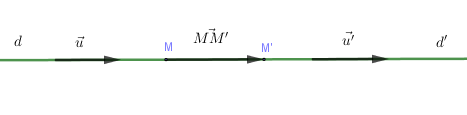
+) (d//d’ Leftrightarrow overrightarrow u ,overrightarrow {u’} ) cùng phương nhưng (overrightarrow u ,overrightarrow {MM’} ) không cùng phương ( Leftrightarrow left{ begin{array}{l}left[ {overrightarrow u ,overrightarrow {u’} } right] = overrightarrow 0 \left[ {overrightarrow u ,overrightarrow {MM’} } right] ne overrightarrow 0 end{array} right.)
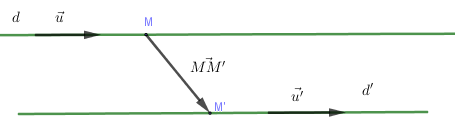
+) (d) cắt (d’ Leftrightarrow overrightarrow u ,overrightarrow {u’} ) không cùng phương và (overrightarrow u ,overrightarrow {u’} ,overrightarrow {MM’} ) đồng phẳng ( Leftrightarrow left{ begin{array}{l}left[ {overrightarrow u ,overrightarrow {u’} } right] ne overrightarrow 0 \left[ {overrightarrow u ,overrightarrow {u’} } right]overrightarrow {MM’} = 0end{array} right.)
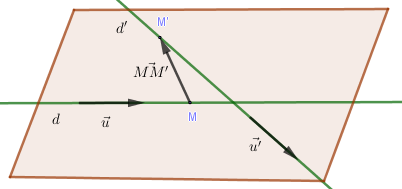
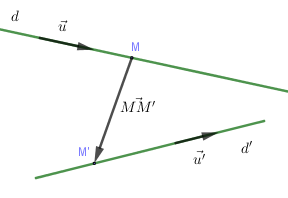
+) (d) chéo (d’ Leftrightarrow overrightarrow u ,overrightarrow {u’} ,overrightarrow {MM’} ) không đồng phẳng ( Leftrightarrow left[ {overrightarrow u ,overrightarrow {u’} } right]overrightarrow {MM’} ne 0)
Ngoài ra, ta có thể giải hệ phương trình của hai đường thẳng để xét vị trí tương đối của hai đường thẳng:
+) Nếu hệ có nghiệm duy nhất thì (d) cắt (d’).
+) Nếu hệ vô số nghiệm thì (d equiv d’).
+) Nếu hệ vô nghiệm thì:
(d//d’) nếu (overrightarrow u = koverrightarrow {u’} ) hay (overrightarrow u ,overrightarrow {u’} ) cùng phương.
(d) chéo (d’) nếu (overrightarrow u ne koverrightarrow {u’} ) hay (overrightarrow u ,overrightarrow {u’} ) không cùng phương.
II. Khoảng cách và góc
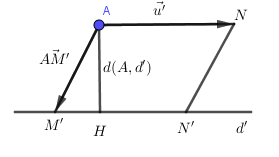
a) Khoảng cách từ điểm (A) đến đường thẳng (d’)
(dleft( {A,d’} right) = dfrac{{{S_{ANN’M’}}}}{{AN}} = dfrac{{left| {left[ {overrightarrow {AM’} ,overrightarrow {u’} } right]} right|}}{{left| {overrightarrow {u’} } right|}})
b) Khoảng cách giữa hai đường thẳng:
(dleft( {Delta ,Delta ‘} right) = dfrac{{left| {left[ {overrightarrow u ,overrightarrow {u’} } right].overrightarrow {MM’} } right|}}{{left| {left[ {overrightarrow u ,overrightarrow {u’} } right]} right|}})
c) Góc giữa hai đường thẳng có các VTCP lần lượt là: (overrightarrow u ,overrightarrow {u’} ):
$cos varphi = left| {cos left( {overrightarrow u ,overrightarrow {u’} } right)} right| = dfrac{{left| {overrightarrow u .overrightarrow {u’} } right|}}{{left| {overrightarrow u } right|.left| {overrightarrow {u’} } right|}}$
