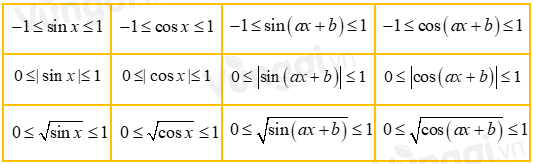I. Hàm số tuần hoàn
Hàm số (y = fleft( x right)) có TXĐ (D) được gọi là hàm số tuần hoàn nếu có số (T ne 0) sao cho:
- a) (forall x in D) đều có (x – T in D,x + T in D).
- b) (forall x in D) đều có (fleft( {x + T} right) = fleft( x right)).
Số (T > 0) nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn (y = fleft( x right)).
II. Các hàm số lượng giác
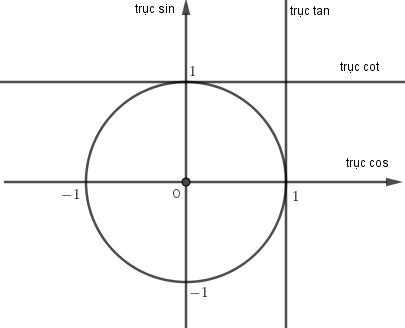
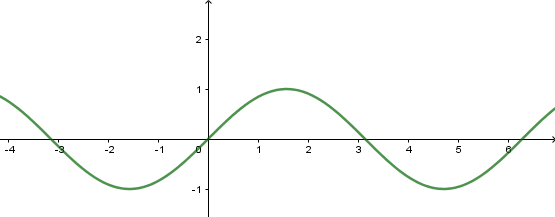
- a) Hàm số (y = sin x)
– Có TXĐ (D = R), là hàm số lẻ, tuần hoàn với chu kì (2pi ), nhận mọi giá trị thuộc đoạn (left[ { – 1;1} right]).
– Đồng biến trên mỗi khoảng (left( { – dfrac{pi }{2} + k2pi ;dfrac{pi }{2} + k2pi } right)) và nghịch biến trên mỗi khoảng (left( {dfrac{pi }{2} + k2pi ;dfrac{{3pi }}{2} + k2pi } right)).
– Có đồ thị là đường hình sin đi qua điểm (Oleft( {0;0} right))
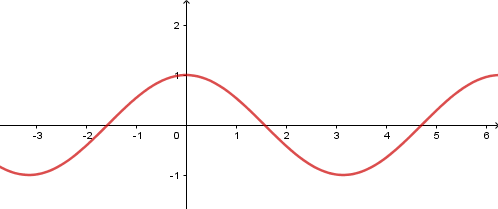
- b) Hàm số (y = cos x)
– Có TXĐ (D = R), là hàm số chẵn, tuần hoàn với chu kì (2pi ), nhận mọi giá trị thuộc đoạn (left[ { – 1;1} right]).
– Đồng biến trên mỗi khoảng (left( { – pi + k2pi ;k2pi } right)) và nghịch biến trên mỗi khoảng (left( {k2pi ;pi + k2pi } right))
– Có đồ thị là đường hình sin đi qua điểm (left( {0;1} right))
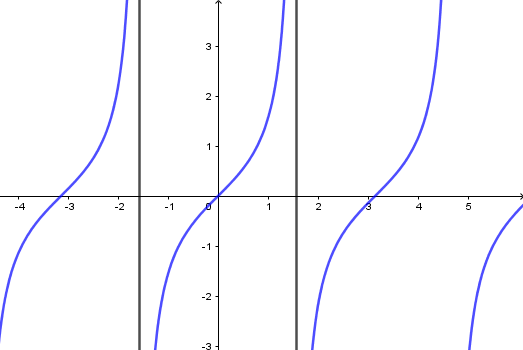
c) Hàm số (y = tan x)
– Có TXĐ (D = Rbackslash left{ {dfrac{pi }{2} + kpi ,k in Z} right}), là hàm số lẻ, tuần hoàn với chu kì (pi ), nhận mọi giá trị thuộc (R).
– Đồng biến trên mỗi khoảng (left( { – dfrac{pi }{2} + kpi ;dfrac{pi }{2} + kpi } right)).
– Đồ thị nhận mỗi đường thẳng (x = dfrac{pi }{2} + kpi ) làm đường tiệm cận.
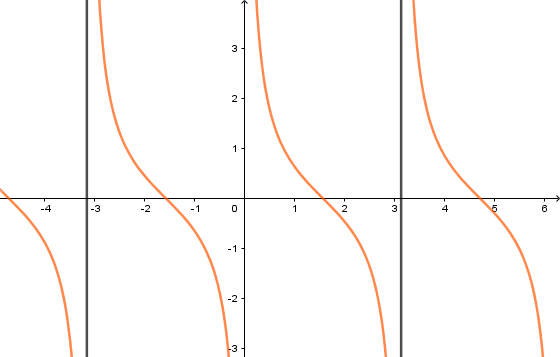
d) Hàm số (y = cot x)
– Có TXĐ (D = Rbackslash left{ {kpi ,k in Z} right}), là hàm số lẻ, tuần hoàn với chu kì (pi ), nhận mọi giá trị thuộc (R).
– Nghịch biến trên mỗi khoảng (left( {kpi ;pi + kpi } right)).
– Đồ thị nhận mỗi đường thẳng (x = kpi ) làm đường tiệm cận.
III. Tìm GTLN, GTNN của hàm số lượng giác
Sử dụng bảng sau để tìm giá trị lớn nhất, nhỏ nhất của các hàm số: