I. Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi một đồ thị quanh trục Ox
Bài toán: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (left( H right)) giới hạn bởi đồ thị hàm số (y = fleft( x right)), trục (Ox) ($y=0$) và hai đường thẳng (x = a,x = bleft( {a < b} right)) quanh trục (Ox)
– Nếu thiếu cận thì giải phương trình $f(x)=0$ để bổ sung cận.
– Công thức tính:
(V = pi intlimits_a^b {{f^2}left( x right)dx} )
Ví dụ: Cho đường cong (y = – {x^2} + 1) và đường thẳng (y = 0). Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi hai đường trên quanh (Ox).
Ta có: ( – {x^2} + 1 = 0 Leftrightarrow left[ begin{array}{l}x = – 1\x = 1end{array} right.)
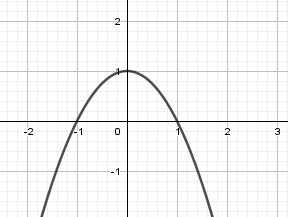
Thể tích: (V = pi intlimits_{ – 1}^1 {{{left( { – {x^2} + 1} right)}^2}dx} = pi intlimits_{ – 1}^1 {left( {{x^4} – 2{x^2} + 1} right)dx} )
$= pi left. {left( {dfrac{{{x^5}}}{5} – dfrac{{2{x^3}}}{3} + x} right)} right|_{ – 1}^1 = dfrac{{16pi }}{{15}}$.
II. Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi một đồ thị quanh trục Oy
Bài toán: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (left( H right)) giới hạn bởi đồ thị hàm số (x = fleft( y right)), trục (Oy) và hai đường thẳng (y = a,y = bleft( {a < b} right)) quanh trục (Oy).
– Giải phương trình $f(y)=0$ để bổ sung cận.
– Công thức tính:
(V = pi intlimits_a^b {{f^2}left( y right)dy} )
III. Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi hai đồ thị quanh trục Ox
Bài toán: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng (left( H right)) giới hạn bởi các đồ thị hàm số (y = fleft( x right),y = gleft( x right)) liên tục trên (left[ {a;b} right],0 le fleft( x right) le gleft( x right),forall x in left[ {a;b} right]) quay quanh trục (Ox)
Công thức tính:
(V = pi intlimits_a^b {left[ {{g^2}left( x right) – {f^2}left( x right)} right]dx} )
IV. Tính thể tích của vật thể biết diện tích thiết diện cắt bởi các mặt phẳng vuông góc với Ox
Bài toán: Tính thể tích của vật thể giới hạn bởi các mặt phẳng (x = a,x = b) biết diện tích thiết diện cắt bởi mặt phẳng vuông góc trục $Ox$ là (S = Sleft( x right)).
Công thức tính:
(V = intlimits_a^b {Sleft( x right)dx} )
Khi miền (D) giới hạn bởi nhiều đồ thị hàm số thì ta nên vẽ hình, sau đó từ hình vẽ suy ra cách tính.
Reader Interactions
