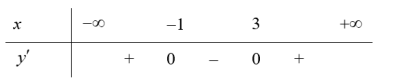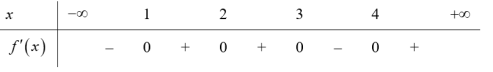Tính đơn điệu của hàm số hợp (nâng cao) – Cách giải và bài tập có đáp
Loại 1: Đổi biến số
Xét bài toán: Tìm m để hàm số $y=fleft[ uleft( x right) right]$ đồng biến hoặc nghịch biến trên $D=left( a;b right)$.
Phương pháp giải tính đơn điệu của hàm số nâng cao
Cách 1: Đặt ẩn phụ: Đặt $t=uleft( x right)Rightarrow {t}’={u}’left( x right),left{ begin{array} {} x=aRightarrow t=uleft( a right) \ {} x=bRightarrow t=uleft( b right) \ end{array} right.$
Nếu ${t}’={u}’left( x right)>0text{ }left( forall xin D right)$ thì bài toán đồng (nghịch) biến trở thành bài toán tìm m để hàm số $y=fleft( t right)$ đồng (nghịch) biến trên ${{D}_{t}}=left( uleft( a right);uleft( b right) right)$.
Nếu ${t}’={u}’left( x right)<0text{ }left( forall xin D right)$ thì bài toán đồng (nghịch) biến trở thành bài toán tìm m để hàm số $y=fleft( t right)$ nghịch (đồng) biến trên ${{D}_{t}}=left( uleft( a right);uleft( b right) right)$.
Cách 2: Tính trực tiếp đạo hàm. Chú ý công thức đạo hàm của hàm hợp: ${y}’={f}’left( u right).{u}’left( x right)$.
Bài tập đồng biến nghịch biến của hàm số nâng cao có đáp án
| Bài tập 1: [Đề minh họa Bộ GD{}ĐT năm 2017] Tìm tất cả các giá trị thực của m để hàm số $y=frac{tan x-1}{tan x-m}$ đồng biến trên khoảng $left( 0;frac{pi }{4} right)$.
A. $left[ begin{array} {} mle 0 \ {} 1le m<2 \end{array} right.$. B. $mle 0$. C. $1le m<2$. D. $mge 2$. |
Lời giải
Cách 1: ĐK: $tan xne m$.
Khi đó ${y}’=frac{-m+2}{{{left( tan x-m right)}^{2}}}.frac{1}{{{cos }^{2}}x}$
Hàm số đồng biến trên khoảng $left( 0;frac{pi }{4} right)Leftrightarrow left{ begin{array} {} tan xne m \ {} frac{-m+2}{{{left( tan x-m right)}^{2}}}.frac{1}{{{cos }^{2}}x}>0 \ end{array} right.left( forall xin left( 0;frac{pi }{4} right) right)$.
$Leftrightarrow left{ begin{array} {} left[ begin{array} {} mle 0 \ {} mge 1 \ end{array} right. \ {} -m+2>0 \ end{array} right.Leftrightarrow left[ begin{array} {} mle 0 \ {} 1le m<2 \ end{array} right.$. Chọn A.
Cách 2: [Đặt ẩn phụ] Đặt $t=tan xRightarrow {t}’=frac{1}{{{cos }^{2}}x}>0text{ }left( forall xin left( 0;frac{pi }{4} right) right)$; với $xin left( 0;frac{pi }{4} right)Rightarrow tin left( 0;1 right)$.
Khi đó bài toán trở thành tìm m để hàm số $fleft( t right)=frac{t-2}{t-m}$ đồng biến trên khoảng $left( 0;1 right)$
$Leftrightarrow left{ begin{array} {} mne t \ {} {f}’left( t right)=frac{-m+2}{{{left( t-m right)}^{2}}}>0left( forall tin left( 0;1 right) right)Leftrightarrow left{ begin{array} {} left[ begin{array} {} mge 1 \ {} mle 0 \ end{array} right. \ {} m<2 \ end{array} right.Leftrightarrow left[ begin{array} {} mle 0 \ {} 1le m<2 \ end{array} right. \ end{array} right.$. Chọn A.
| Bài tập 2: Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=frac{mcos x-2}{2cos x-m}$ nghịch biến trên khoảng $left( frac{pi }{3};frac{pi }{2} right)$.
A. $-2<mle 0$ hoặc $1le m<2$. B. $1le m<2$. C. $-2<mle 0$. D. $mge 2$. |
Lời giải
Ta có: ${y}’=frac{-{{m}^{2}}+4}{{{left( 2cos x-m right)}^{2}}}.left( -sin x right)=frac{left( {{m}^{2}}-4 right)sin x}{{{left( 2cos x-m right)}^{2}}}$
Hàm số đã cho nghịch biến trên $left( frac{pi }{3};frac{pi }{2} right)Leftrightarrow {y}'<0text{ }left( forall xin left( frac{pi }{3};frac{pi }{2} right) right)Leftrightarrow left{ begin{array} {} {{m}^{2}}-4<0 \ {} 2cos xne mtext{ }left( forall xin left( frac{pi }{3};frac{pi }{2} right) right) \ end{array} right.$
$Leftrightarrow left{ begin{array} {} -2<m<2 \ {} mnotin left( 0;1 right) \ end{array} right.Leftrightarrow left{ begin{array} {} -2<mle 0 \ {} 1le m<2 \ end{array} right.$. Chọn A.
| Bài tập 3: Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=frac{cos x-2}{cos x-m}$ nghịch biến trên khoảng $left( -frac{pi }{2};0 right)$.
A. $mle 0$ hoặc $1le m<2$. B. $mle 0$. C. $1le m<2$ D. $mge 2$. |
Lời giải
Ta có: ${y}’=frac{-m+2}{{{left( mcos x-1 right)}^{2}}}.sin x$. Do đó $sin x0 \ {} mnotin left( 0;1 right) \ end{array} right.Leftrightarrow left{ begin{array} {} m<2 \ {} left[ begin{array} {} mge 1 \ {} mle 0 \ end{array} right. \ end{array} right.Leftrightarrow left[ begin{array} {} mle 0 \ {} 1le m<2 \ end{array} right.$. Chọn A.
| Bài tập 4: Tìm tất cả các giá trị của tham số m sao cho hàm số $y=frac{2cos x+3}{2cos x-m}$ nghịch biến trên khoảng $left( 0;frac{pi }{3} right)$.
A. $m>-3$. B. $left[ begin{array} {} mle -3 \ {} mge 2 \ end{array} right.$. C. $m<-3$. D. $left[ begin{array} {} -3<mle 1 \ {} mge 2 \ end{array} right.$. |
Lời giải
Ta có: ${y}’={{left( frac{2cos x+3}{2cos x-m} right)}^{prime }}=frac{left( 2m+6 right)sin x}{{{left( 2cos x-m right)}^{2}}}$.
Hàm số nghịch biến trên khoảng $left( 0;frac{pi }{3} right)Rightarrow left{ begin{array} {} {y}'<0 \ {} xin left( 0;frac{pi }{3} right) \ end{array} right.Rightarrow left{ begin{array} {} left( 2m+6 right)sin x<0 \ {} xin left( 0;frac{pi }{3} right) \ end{array} right.$
$Leftrightarrow 2m+6<0Leftrightarrow m<-3$.Mặt khác $left{ begin{array} {} 2cos x-mne 0 \ {} xin left( 0;frac{pi }{3} right) \ end{array} right.Leftrightarrow left{ begin{array} {} mne 2cos x \ {} cos xin left( -frac{1}{2};1 right) \ end{array} right.Leftrightarrow mnotin left( -1;2 right)Rightarrow m<-3$. Chọn C.
| Bài tập 5: Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=frac{cot x-1}{mcot x-1}$ đồng biến trên khoảng $left( frac{pi }{4};frac{pi }{2} right)$.
A. $min left( -infty ;0 right)cup left( 1;+infty right)$. B. $min left( 1;+infty right)$. C. $min left( -infty ;0 right)$. D. $min left( -infty ;1 right)$. |
Lời giải
Ta có: ${y}’=frac{-1+m}{{{left( mcot x-1 right)}^{2}}}.left( -frac{1}{{{sin }^{2}}x} right)$
+ Với $m=0Rightarrow y=1-cot xRightarrow {y}’=frac{1}{{{sin }^{2}}x}>0Rightarrow $ Hàm số đồng biến trên khoảng $left( frac{pi }{4};frac{pi }{2} right)$.
+ Với $mne 0$, hàm số đồng biến trên khoảng $left( frac{pi }{4};frac{pi }{2} right)Leftrightarrow left{ begin{array} {} {y}’>0 \ {} cot xne frac{1}{m} \ end{array} right.left( forall xin left( frac{pi }{4};frac{pi }{2} right) right)$
$Leftrightarrow left{ begin{array} {} 1-m>0 \ {} frac{1}{m}notin left( 0;1 right) \ end{array} right.Leftrightarrow left{ begin{array} {} m<1 \ {} left[ begin{array} {} frac{1}{m}le 0 \ {} frac{1}{m}ge 1 \ end{array} right. \ end{array} right.Leftrightarrow left{ begin{array} {} m<1 \ {} mne 0 \ end{array} right.$.
Kết hợp 2 trường hợp suy ra $m<1$ là giá trị cần tìm. Chọn D.
| Bài tập 6: Có bao nhiêu giá trị nguyên m để hàm số $y=frac{m{{sin }^{2}}x-16}{{{cos }^{2}}x+m-1}$ nghịch biến trên khoảng $left( 0;frac{pi }{2} right)$.
A. 5. B. 8. C. 7. D. 6. |
Lời giải
Ta có: $y=frac{m{{sin }^{2}}x-16}{{{cos }^{2}}x+m-1}=frac{m{{sin }^{2}}x-16}{-{{sin }^{2}}x+m}text{ }left( text{Do }{{cos }^{2}}x-1=-{{sin }^{2}}x right)$
Khi đó ${y}’=frac{{{m}^{2}}-16}{{{left( -{{sin }^{2}}x+m right)}^{2}}}.{{left( {{sin }^{2}}x right)}^{prime }}=frac{{{m}^{2}}-16}{{{left( -{{sin }^{2}}x+m right)}^{2}}}.2sin xcos x$
Do $2sin xcos x>0text{ }left( forall xin left( 0;frac{pi }{2} right) right)$ do đó hàm số đã cho nghịch biến trên khoảng
$left( 0;frac{pi }{2} right)Leftrightarrow left{ begin{array} {} {{m}^{2}}-16<0 \ {} {{sin }^{2}}xne mtext{ }left( forall xin left( 0;frac{pi }{2} right) right) \ end{array} right.Leftrightarrow left{ begin{array} {} -4<m<4 \ {} mnotin left( 0;1 right) \ end{array} right.$.
Kết hợp ![]() có 7 giá trị của m. Chọn C.
có 7 giá trị của m. Chọn C.
| Bài tập 7: Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=frac{msqrt{1-x}-4}{sqrt{1-x}-m}$ đồng biến trên khoảng $left( 0;1 right)$.
A. $left[ begin{array} {} m2 \ end{array} right.$. B. $-2<m<2$. C. $left[ begin{array} {} -2<mle 0 \ {} 1le m<2 \ end{array} right.$. D. $left[ begin{array} {} -2<m<0 \ {} 1<m<2 \ end{array} right.$. |
Lời giải
Đặt $t=sqrt{1-x}Rightarrow {t}’=frac{-1}{2sqrt{1-x}}<0text{ }left( forall xin left( 0;1 right) right)$ với $xin left( 0;1 right)Rightarrow tin left( 0;1 right)$
Khi đó bài toán trở thành tìm m để hàm số $fleft( t right)=frac{mt-4}{t-m}$ nghịch biến trên khoảng $left( 0;1 right)$.
$Leftrightarrow left{ begin{array} {} mne t \ {} {f}’left( t right)=frac{-{{m}^{2}}+4}{{{left( t-m right)}^{2}}}2 \ {} m2 \ {} m<-2 \ end{array} right.$. Chọn A.
| Bài tập 8: Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=frac{sqrt{1-5x}-2}{sqrt{1-5x}-m}$ nghịch biến trên khoảng $left( 0;frac{1}{5} right)$.
A. $left[ begin{array} {} mle 0 \ {} 1le m<2 \ end{array} right.$ B. $mle 0$ C. $1le m<2$ D. $m>2$ |
Lời giải
Đặt $t=sqrt{1-5x}Rightarrow {t}’=frac{-5}{2sqrt{1-5x}}<0text{ }left( forall xin left( 0;frac{1}{5} right) right)$ với $xin left( 0;frac{1}{5} right)Rightarrow tin left( 0;1 right)$
Khi đó bài toán trở thành tìm m để hàm số $fleft( t right)=frac{t-2}{t-m}$ đồng biến trên khoảng $left( 0;1 right)$.
..$Leftrightarrow left{ begin{array} {} mne t \ {} {f}’left( t right)=frac{-m+2}{{{left( t-m right)}^{2}}}>0 \ end{array} right.left( forall tin left( 0;1 right) right)Leftrightarrow left{ begin{array} {} left[ begin{array} {} mge 1 \ {} mle 0 \ end{array} right. \ {} m<2 \ end{array} right.Leftrightarrow left[ begin{array} {} mle 0 \ {} 1le m<2 \ end{array} right.$. Chọn A.
| Bài tập 9: Tìm tất cả các giá trị của tham số m sao cho hàm số $y=mleft( {{x}^{2}}-2x right)-frac{4}{3}left( x-3 right)sqrt{x-3}-x$ luôn đồng biến trên tập xác định.
A. $mge frac{2}{3}$. B. $mge frac{1}{2}$. C. $mge frac{4}{3}$. D. $mge frac{3}{2}$. |
Lời giải
Ta có: $y=mleft( {{x}^{2}}-2x right)-frac{4}{3}left( x-3 right)sqrt{x-3}-xto {y}’=2mleft( x-1 right)-2sqrt{x-3}-1;text{ }forall xge 3$
Đặt $t=sqrt{x-3}ge 0Rightarrow {t}’=frac{1}{2sqrt{x-3}}>0left( forall x>3 right)Leftrightarrow x={{t}^{2}}+3$, khi đó ${y}’=fleft( t right)=2mleft( {{t}^{2}}+2 right)-2t-1$.
Để hàm số đồng biến trên tập xác định $fleft( t right)>0;text{ }forall tge 0Leftrightarrow 2mleft( {{t}^{2}}+2 right)ge 2t+1;text{ }forall tge 0$.
$Leftrightarrow 2mge frac{2t+1}{{{t}^{2}}+2};text{ }forall tge 0Rightarrow 2mge underset{left[ 0;+infty right)}{mathop{max }},gleft( t right)$ với hàm số $gleft( t right)=frac{2t+1}{{{t}^{2}}+2}$
Mặt khác $gleft( t right)-1=frac{2t+1}{{{t}^{2}}+2}-1=-frac{{{left( t-1 right)}^{2}}}{{{t}^{2}}+2}le 0Leftrightarrow gleft( t right)le 1Rightarrow underset{left[ 0;+infty right)}{mathop{max }},gleft( t right)=1$
Vậy $2mge 1Leftrightarrow mge frac{1}{2}$ là giá trị cần tìm. Chọn B.
Loại 2: Tính đồng biến, nghịch biến của hàm số hợp cho trực tiếp
Phương pháp giải:
Công thức đạo hàm của hàm hợp ${{left[ fleft( u right) right]}^{prime }}={f}’left( u right).{u}’$.
Lập bảng xét dấu ${y}’$ của hàm số đã cho và kết luận.
Bài tập minh họa
| Bài tập 1: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)={{left( x-1 right)}^{2}}left( 2x-1 right)left( x+1 right)$ trên $mathbb{R}$.
a) Tìm khoảng đồng biến của hàm số $gleft( x right)=fleft( 1-2x right)$. b) Tìm khoảng nghịch biến của hàm số $hleft( x right)=fleft( x+3 right)$.. |
Lời giải
a) Ta có: ${g}’left( x right)={{left[ fleft( 1-2x right) right]}^{prime }}={f}’left( 1-2x right).{{left( 1-2x right)}^{prime }}=-2{{left( 1-2x-1 right)}^{2}}left[ 2left( 1-2x right)-1 right]left( 1-2x+1 right)$
$Rightarrow {g}’left( x right)=-8{{x}^{2}}left( 1-4x right)left( 2-2x right)=-16{{x}^{2}}left( 4x-1 right)left( x-1 right)$
Bảng xét dấu cho ${g}’left( x right)$.
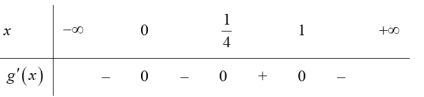
Vậy hàm số $gleft( x right)$ đồng biến trên khoảng $left( frac{1}{4};1 right)$.
b) Ta có: ${h}’left( x right)={{left[ fleft( x+3 right) right]}^{prime }}={f}’left( x+3 right).{{left( x+3 right)}^{prime }}={{left( x+3-1 right)}^{2}}left[ 2left( x+3 right)-1 right]left( x+3+1 right)$
$Rightarrow {h}’left( x right)={{left( x+2 right)}^{2}}left( 2x+5 right)left( x+4 right)<0$
Bảng xét dấu cho ${h}’left( x right)$
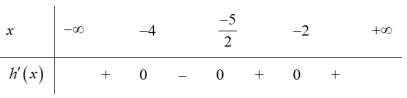
Vậy hàm số $hleft( x right)$ nghịch biến trên khoảng $left( -4;frac{-5}{2} right)$.
| Bài tập 2: Cho hàm số $y=fleft( x right)$ có đạo hàm trên $mathbb{R}$ và ${f}’left( x right)=left( x+1 right)left( x-2 right)$.
a) Xét tính đồng biến và nghịch biến của hàm số $gleft( x right)=fleft( {{x}^{2}}-2 right)$. b) Xét tính đồng biến và nghịch biến của hàm số $hleft( x right)=fleft( 1-x right)+frac{3{{x}^{2}}}{2}-5x+1$. |
Lời giải
a) Ta có: ${g}’left( x right)=2x.{f}’left( {{x}^{2}}-2 right)=2x.left( {{x}^{2}}-2+1 right)left( {{x}^{2}}-2-2 right)=2x.left( {{x}^{2}}-1 right)left( {{x}^{2}}-4 right)$.
Bảng xét dấu cho ${g}’left( x right)$.
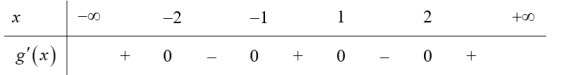
Vậy hàm số $gleft( x right)$ đồng biến trên các khoảng $left( -infty ;-2 right)$; $left( 1;1 right)$ và $left( 2;+infty right)$. Vậy hàm số $gleft( x right)$ nghịch biến trên các khoảng $left( -2;-1 right)$ và $left( 1;2 right)$.
b) Ta có: ${h}’left( x right)=left[ {f}’left( 1-x right) right]+3x-5=-{f}’left( 1-x right)+3x-5=-left( 1-x+1 right)left( 1-x-2 right)+3x-5$
$=left( x-2 right)left( -1-x right)+3x-5=-{{x}^{2}}+4x-3=-left( x-1 right)(x-3)$.
Bảng xét dấu cho ${h}’left( x right)$
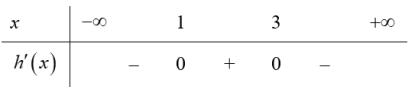
Vậy hàm số $hleft( x right)$ đồng biến trên khoảng $left( 1;3 right)$ và nghịch biến trên các khoảng $left( -infty ;1 right)$ và $left( 3;+infty right)$.
| Bài tập 3: Cho hàm số $y=fleft( x right)$ có đạo hàm trên $mathbb{R}$ và ${f}’left( x right)={{x}^{2}}-x$.
a) Tìm .khoảng đơn điệu của hàm số $gleft( x right)=fleft( 2x+1 right)-12x$. b) Tìm khoảng đơn điệu của hàm số $hleft( x right)=fleft( {{x}^{2}} right)+frac{16{{x}^{3}}}{3}-16x+2$. |
Lời giải
a) Ta có: ${g}’left( x right)=2{f}’left( 2x+1 right)-12=2.left[ {{left( 2x+1 right)}^{2}}-left( 2x+1 right) right]-12$
$=2left( 4{{x}^{2}}+2x-6 right)=4left( 2x+3 right)left( x-1 right)$
Bảng xét dấu cho ${g}’left( x right)$.
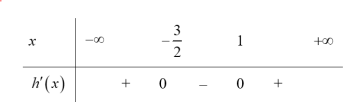
Vậy hàm số đồng biến trên mỗi khoảng $left( -infty ;-frac{3}{2} right)$ và $left( 1;+infty right)$, hàm số nghịch biến trên khoảng $left( -frac{3}{2};1 right)$.
b) Ta có: ${h}’left( x right)=2x.{f}’left( {{x}^{2}} right)=2x({{x}^{4}}-{{x}^{2}})+16{{x}^{2}}-16=2{{x}^{3}}left( {{x}^{2}}-1 right)+16left( {{x}^{2}}-1 right)=2left( {{x}^{2}}-1 right)left( {{x}^{3}}+8 right)$
Bảng xét dấu cho ${h}’left( x right)$.
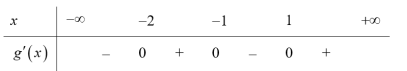
Vậy hàm số đồng biến trên khoảng $left( -2;-1 right)$ và $left( 1;+infty right)$, hàm số nghịch biến trên khoảng $left( -infty ;-2 right)$ và $left( -1;1 right)$.
| Bài tập 4: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)=left( x-2 right)left( 2x-5 right)text{ }forall xin mathbb{R}$. Tìm khoảng đồng biến của hàm số $y=fleft( {{x}^{2}}+2 right)-frac{1}{2}{{x}^{4}}+2$
A. $left( -1;1 right)$. B. $left( 0;2 right)$. C. $left( 1;+infty right)$. D. $left( -3;0 right)$. |
Lời giải
Ta có: $y=fleft( {{x}^{2}}+2 right)-frac{1}{2}{{x}^{4}}+2Rightarrow {y}’=2x.{f}’left( {{x}^{2}}+2 right)-2{{x}^{3}}=2x.{{x}^{2}}left( 2{{x}^{2}}+4-5 right)-2{{x}^{3}}$
$=2{{x}^{3}}left( 2{{x}^{2}}-2 right)=4{{x}^{3}}left( x-1 right)left( x+1 right)$.
Bảng xét dấu cho ${y}’$.
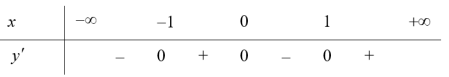
Dựa vào bảng xét dấu suy ra hàm số đồng biến trên khoảng $left( 1;+infty right)$. Chọn C.
| Bài tập 5: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)={{x}^{3}}{{left( x-1 right)}^{2}}left( 2x-1 right)$ trên $mathbb{R}$ và hàm số $gleft( x right)=fleft( x+2 right)$. Hàm số $gleft( x right)$ nghịch biến trên khoảng nào sau đây:
A. $left( -infty ;-2 right)$. B. $left( -2;-frac{3}{2} right)$. C. $left( 2;frac{3}{2} right)$. D. $left( frac{3}{2};+infty right)$. |
Lời giải
Ta có: ${g}’left( x right)={{left[ fleft( x+2 right) right]}^{prime }}={{left( x+2 right)}^{3}}{{left( x+2-1 right)}^{2}}left[ 2left( x+2 right)-1 right]$
$={{left( x+2 right)}^{3}}{{left( x+1 right)}^{2}}.left( 2x+3 right)<0Leftrightarrow left( x+2 right)left( 2x+3 right)<0Leftrightarrow -2<x<-frac{3}{2}$.
Suy ra hàm số $gleft( x right)$ nghịch biến trên khoảng $left( -2;-frac{3}{2} right)$. Chọn B.
| Bài tập 6: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)=left( {{x}^{2}}+x right){{left( x-2 right)}^{2}}$ trên $mathbb{R}$ và hàm số $gleft( x right)=fleft( {{x}^{2}}-1 right)$. Hàm số $gleft( x right)$ đồng biến trên khoảng nào sau đây:
A. $left( -1;0 right)$. B. $left( 0;1 right)$. C. $left( -2;-1 right)$. D. $left( -1;1 right)$. |
Lời giải
Ta có: ${f}’left( x right)=left( {{x}^{2}}+x right){{left( x-2 right)}^{2}}=xleft( x+1 right){{left( x-2 right)}^{2}}$
Khi đó ${g}’left( x right)={{left[ fleft( {{x}^{2}}-1 right) right]}^{prime }}={{left( {{x}^{2}}-1 right)}^{prime }}.{f}’left( {{x}^{2}}-1 right)$
$=2xleft( {{x}^{2}}-1 right).{{x}^{2}}{{left[ left( {{x}^{2}}-1 right)-2 right]}^{2}}>0Leftrightarrow xleft( {{x}^{2}}-1 right)>0Leftrightarrow left[ begin{array} {} x>1 \ {} -1<x<0 \ end{array} right.$
Suy ra hàm số $gleft( x right)$ đồng biến trên khoảng $left( -1;0 right)$. Chọn A.
| Bài tập 7: Cho hàm số $y=fleft( x right)$ liên tục và xác định trên $mathbb{R}$, biết rằng ${f}’left( x right)={{x}^{2}}+x$, hàm số $y=fleft( {{x}^{2}}-1 right)$ đồng biến trên khoảng nào sau đây?
A. $left( 1;2 right)$. B. $left( -1;1 right)$. C. $left( 0;1 right)$. D. $left( -infty ;-1 right)$. |
Lời giải
Ta có công thức đạo hàm của hàm hợp ${{left[ fleft( u right) right]}^{prime }}={f}’left( u right).{u}’left( x right)$.
Do đó ${{left[ fleft( {{x}^{2}}-1 right) right]}^{prime }}={f}’left( {{x}^{2}}-1 right).2x=2left( {{x}^{2}}-1 right){{x}^{3}}$.
Vẽ bảng xét dấu ta có: ${{left[ fleft( {{x}^{2}}-1 right) right]}^{prime }}>0Leftrightarrow left[ begin{array} {} x>1 \ {} -1<x<0 \ end{array} right.$.
Do đó hàm số $y=fleft( {{x}^{2}}-1 right)$ đồng biến trên khoảng $left( -1;0 right)$ và $left( 1;+infty right)$. Chọn A.
| Bài tập 8: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)=x{{left( x-1 right)}^{2}}left( x-2 right)$. Hỏi hàm số $y=fleft( frac{5x}{{{x}^{2}}+4} right)$ đồng biến trên khoảng nào dưới đây?
A. $left( -infty ;-2 right)$. B. $left( 0;2 right)$. C. $left( 2;4 right)$. D. $left( -2;1 right)$. |
Lời giải
Ta có: ${{left( frac{5x}{{{x}^{2}}+4} right)}^{prime }}=5.frac{{{x}^{2}}+4-2{{x}^{2}}}{{{left( {{x}^{2}}+4 right)}^{2}}}=5.frac{4-{{x}^{2}}}{{{left( {{x}^{2}}+4 right)}^{2}}}$.
Xét hàm số: $y=fleft( frac{5x}{{{x}^{2}}+4} right)Rightarrow {y}’=5.frac{4-{{x}^{2}}}{{{left( {{x}^{2}}+4 right)}^{2}}}.frac{5x}{{{x}^{2}}+4}{{left( frac{5x}{{{x}^{2}}+4}-1 right)}^{2}}left( frac{5x}{{{x}^{2}}+4}-2 right)>0$
$Leftrightarrow left( 4-{{x}^{2}} right)x.left( 5x-2{{x}^{2}}-8 right)>0Leftrightarrow left( x+2 right)x(x-2)left( 2{{x}^{2}}-5x+8 right)>0$
$Leftrightarrow left( x+2 right)x(x-2)>0Leftrightarrow left[ begin{array} {} x>2 \ {} -2<x<0 \ end{array} right.$.
Vậy hàm số $y=fleft( frac{5x}{{{x}^{2}}+4} right)$ đồng biến trên khoảng $left( 2;+infty right)$ nên nó đồng biến trên khoảng $left( 2;4 right)$.
Chọn C.
| Bài tập 9: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)={{x}^{2}}+x-2text{ }forall xin mathbb{R}$. Tìm khoảng nghịch biến của hàm số $y=fleft( {{x}^{2}} right)-18{{x}^{2}}+2$
A. $left( 0;1 right)$. B. $left( -2;0 right)$. C. $left( 1;3 right)$. D. $left( 2;+infty right)$. |
Lời giải
Ta có: $y=fleft( {{x}^{2}} right)-18{{x}^{2}}+2Rightarrow {y}’=2x.{f}’left( {{x}^{2}} right)-36x=2x.left[ {f}’left( {{x}^{2}} right)-18 right]$
$Leftrightarrow 2xleft( {{x}^{4}}+{{x}^{2}}-2-18 right)=2xleft( {{x}^{2}}-4 right)left( {{x}^{2}}+5 right)$.
Bảng xét dấu cho ${y}’$
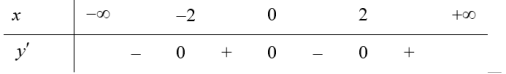
Dựa vào bảng xét dấu suy ra hàm số nghịch biến trên khoảng $left( 0;2 right)$. Chọn A.
| Bài tập 10: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)={{x}^{2}}left( x-1 right)left( {{x}^{2}}-4 right)$. Hàm số $y=fleft( 2-x right)$ đồng biến trên khoảng nào?
A. $left( -infty ;0 right)$. B. $left( 0;1 right)$. C. $left( 2;+infty right)$. D. $left( 1;4 right)$. |
Lời giải
Ta có: ${f}’left( x right)={{x}^{2}}left( x-1 right)left( {{x}^{2}}-4 right)={{x}^{2}}left( x-1 right)left( x-2 right)left( x+2 right)$.
Khi đó: $y=fleft( 2-x right)Rightarrow {y}’=-{{left( 2-x right)}^{2}}left( 1-x right)left( -x right)left( 4-x right)={{left( x-2 right)}^{2}}xleft( x-1 right)left( x-4 right)>0$
$Leftrightarrow xleft( x-1 right)left( x-4 right)>0Leftrightarrow left[ begin{array} {} x>4 \ {} 0<x<1 \ end{array} right.$.
Vậy hàm số $y=fleft( 2-x right)$ đồng biến trên khoảng $left( 0;1 right)$. Chọn B.
| Bài tập 11: Cho hàm số $y=fleft( x right)$ có đạo hàm ${f}’left( x right)=left( x+3 right)left( {{x}^{2}}+x right)$. Hàm số $gleft( x right)=fleft( {{x}^{2}}+2x right)+frac{{{x}^{4}}}{2}+2{{x}^{3}}+2{{x}^{2}}$ đồng biến trên khoảng nào sau đây?
A. $left( -2;-1 right)$. B. $left( -1;0 right)$. C. $left( 0;1 right)$. D. $left( -4;-3 right)$. |
Lời giải
Ta có: ${f}’left( x right)=left( x+3 right)left( {{x}^{2}}+x right);{g}’left( x right)=left( 2x+2 right).{f}’left( {{x}^{2}}+2x right)+2{{x}^{3}}+6{{x}^{2}}+4x$
$=2left( x+1 right)left( {{x}^{2}}+2x+3 right)left( {{x}^{2}}+2x right)left( {{x}^{2}}+2x+1 right)+2xleft( {{x}^{2}}+3x+2 right)$
$=2xleft( x+1 right)left( x+2 right)left[ left( {{x}^{2}}+2x+3 right)left( {{x}^{2}}+2x+1 right)+1 right]$
Do ${{x}^{2}}+2x+1={{left( x+1 right)}^{2}}ge 0text{ }left( forall xin mathbb{R} right)$ nên $left( {{x}^{2}}+2x+3 right)left( {{x}^{2}}+2x+1 right)+1>0text{ }left( forall xin mathbb{R} right)$
Do đó ${g}’left( x right)>0Leftrightarrow xleft( x+1 right)left( x+2 right)>0Leftrightarrow left[ begin{array} {} x>0 \ {} -2<x<-1 \ end{array} right.$.
Vậy $gleft( x right)$ đồng biến trên khoảng $left( -2;-1 right)$ và $left( 1;+infty right)$. Chọn A.
| Bài tập : Cho hàm số $y=fleft( x right)$ có đạo hàm cấp 2 xác định và liên tục trên $mathbb{R}$ thỏa mãn ${{left( {f}’left( x right) right)}^{2}}+fleft( x right){{f}’}’left( x right)=xleft( x-1 right)left( x-2 right),forall xin mathbb{R}$. Hàm số $gleft( x right)=fleft( x right).{f}’left( x right)$ đồng biến trên khoảng nào?
A. $left( 0;2 right)$. B. $left( -infty ;0 right)$. C. $left( 2;+infty right)$. D. $left( 1;2 right)$. |
Lời giải
Ta có: ${g}’left( x right)={{left[ fleft( x right).{f}’left( x right) right]}^{prime }}=fleft( x right).{{f}’}’left( x right)+{{f}^{2′}}left( x right)=xleft( x-1 right)left( x-2 right)>0Leftrightarrow left[ begin{array} {} x>1 \ {} 0<x<1 \ end{array} right.$.
Do đó hàm số $gleft( x right)$ đồng biến trên khoảng $left( 1;+infty right)$ nên nó đồng biến trên khoảng $left( 2;+infty right)$. Chọn C.
| Bài tập : Cho hàm số $y=fleft( x right)$ liên tục và có đạo hàm ${f}’left( x right)=x{{left( x-1 right)}^{2}}left( {{x}^{2}}+mx+16 right)$. Có bao nhiêu số nguyên dương của tham số m để hàm số $y=fleft( 4-x right)$ đồng biến trên khoảng $left( 4;+infty right)$?
A. 6. B. 8. C. 5. D. 7. |
Lời giải
Ta có: $y=fleft( 4-x right)Rightarrow {y}’=-left( 4-x right){{left( 3-x right)}^{2}}left( {{t}^{2}}+mt+16 right)$ với $t=4-x,text{ }x>4Rightarrow t<0$.
Hàm số đồng biến trên khoảng $left( 4;+infty right)Leftrightarrow left( x-4 right){{left( x-3 right)}^{2}}left[ {{t}^{2}}+mt+16 right]ge 0left( forall xin left( 4;+infty right) right)$
$Leftrightarrow {{t}^{2}}+mt+16ge 0text{ }left( forall t<0 right)Leftrightarrow {{t}^{2}}+16ge -mttext{ }left( forall t<0 right)Leftrightarrow -t+frac{-16}{t}ge mtext{ }left( forall t<0 right)$
$Leftrightarrow underset{left( -infty ;0 right)}{mathop{min }},gleft( t right)ge m$, với $gleft( t right)=-t-frac{16}{t}$
Mặt khác theo BĐT AM – GM ta có: $gleft( t right)ge 2sqrt{-t.left( frac{-16}{t} right)}=8Rightarrow mle 8$ là giá trị cần tìm.
Kết hợp $min {{mathbb{Z}}^{+}}Rightarrow $ có 8 giá trị nguyên dương của m. Chọn B.
Loại 3: Tính đồng biến, nghịch biến của hàm số hợp cho qua bảng biến thiên hoặc đồ thị.
Phương pháp giải:
Giả sử giả thiết bài toán cho đồ thị hàm ${f}’left( x right)$ với mọi $xin mathbb{R}$ như hình vẽ dưới đây.
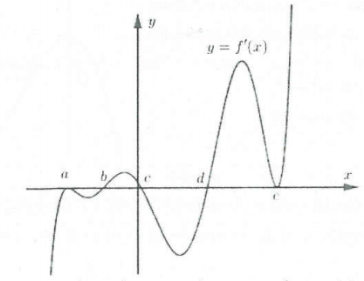
Đối với bài toán tìm khoảng đồng biến nghịch biến của hàm số $y=fleft( x right)$ ta dựa đồ thị ${f}’left( x right)$như hình vẽ để tìm khoảng đồng biến nghịch biến.
Đối với bài toán tìm khoảng đồng biến nghịch biến của hàm hợp $y=fleft( u right)$ ta làm như sau:
Ta thấy ${f}’left( x right)$ đổi dấu qua các điểm $x=b,text{ }x=c,text{ }x=d$ và ${f}’left( x right)$ bằng không nhưng không đổi dấu tại các điểm $x=a,text{ }x=e$ nên ta có thể thiết lập biểu thức đạo hàm:
${f}’left( x right)=k{{left( x-a right)}^{2}}left( x-b right)left( x-c right)left( x-d right){{left( x-e right)}^{2}}$
Trong đó hệ số $k>0$ nếu $underset{xto +infty }{mathop{lim }},{f}’left( x right)>0$ và $k<0$ nếu $underset{xto +infty }{mathop{lim }},{f}’left( x right)0$ (vì khi $xto +infty $ thì ${f}’left( x right)>0$ nên ta có thể giả sử:
${f}’left( x right)={{left( x-a right)}^{2}}left( x-b right)left( x-c right)left( x-d right){{left( x-e right)}^{2}}$ từ đó suy ra đạo hàm của hàm hợp ${{left[ fleft( u right) right]}^{prime }}={u}’.{f}’left( u right)$. Từ đó lập bảng xét dấu và kết luận.
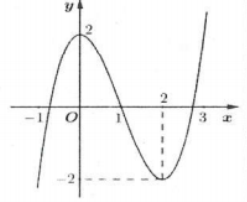
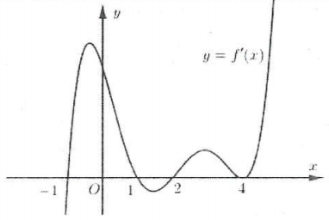
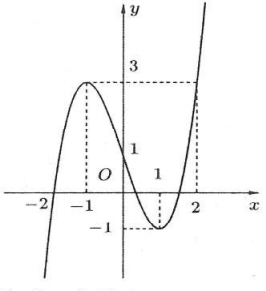
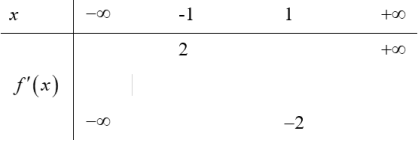
| Bài tập 1: Cho hàm số $y=fleft( x right)$. Hàm số $y={f}’left( x right)$ có đồ thị như hình bên. Hỏi hàm số đã cho nghịch biến trên khoảng nào sau đây?
A. $left( 0;2 right)$. B. $left( 1;3 right)$. C. $left( -1;1 right)$. D. $left( -infty ;2 right)$. |
Lời giải
Dựa vào đồ thị hàm số $y={f}’left( x right)$ ta thấy $1<x<3$ thì đồ thị hàm số $y={f}’left( x right)$ nằm ở dưới trục hoành nên ${f}’left( x right)<0Rightarrow $ hàm số $y=fleft( x right)$ nghịch biến trên khoảng $left( 1;3 right)$. Chọn B.
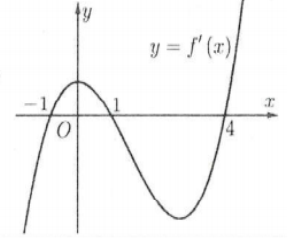
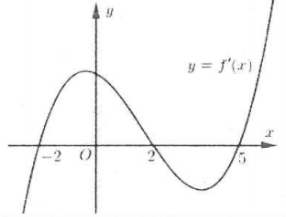
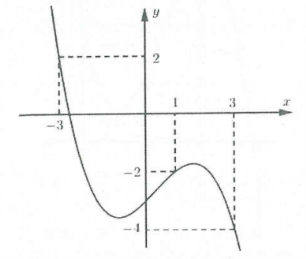
| Bài tập 2: [Đề thi minh họa của Bộ GD{}ĐT năm 2018] Cho hàm số $y=fleft( x right)$. Hàm số $y={f}’left( x right)$ có đồ thị như hình bên. Hỏi hàm số $y=fleft( 2-x right)$ đồng biến trên khoảng nào sau đây?
A. $left( 1;3 right)$. B. $left( 2;+infty right)$. C. $left( -2;1 right)$. D. $left( -infty ;-2 right)$. |
Lời giải
Cách 1: Giả sử ${f}’left( x right)=left( x+1 right)left( x-1 right)left( x-4 right)$ ta có: ${{left[ fleft( 2-x right) right]}^{prime }}={f}’left( 2-x right).{{left( 2-x right)}^{prime }}$
$=-{f}’left( 2-x right)=-left( 2-x+1 right)left( 2-x-1 right)left( 2-x-4 right)=left( x-3 right)left( x-1 right)left( x+2 right)>0$.
Bảng xét dấu ${{left[ fleft( 2-x right) right]}^{prime }}$
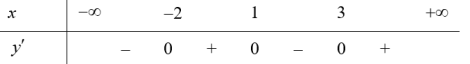
Vậy hàm số đồng biến trên $left( -2;1 right)$ và $left( 3;+infty right)$.
Cách 2: Ta có: ${{left[ fleft( 2-x right) right]}^{prime }}={f}’left( 2-x right).{{left( 2-x right)}^{prime }}=-{f}’left( 2-x right)>0Leftrightarrow {f}’left( 2-x right)<0$
Dựa vào đồ thị ta có: ${f}’left( 2-x right)<0Leftrightarrow left[ begin{array} {} 2-x<-1 \ {} 1<2-x3 \ {} -2<x<1 \ end{array} right.$.
Vậy hàm số đồng biến trên ![]() . Chọn C.
. Chọn C.
| Bài tập 3: Cho hàm số $y=fleft( x right)$ có bảng xét dấu như sau:
Hàm số $y=fleft( {{x}^{2}}-2 right)$ nghịch biến trên khoảng nào dưới đây? A. $left( -2;0 right)$. B. $left( 2;+infty right)$. C. $left( 0;2 right)$. D. $left( -infty ;-2 right)$. |
Lời giải
Dựa vào bảng xét dấu ta có thể giả sử ${f}’left( x right)=-left( x+2 right)xleft( x-2 right)$
(Chú ý: Do $underset{xto +infty }{mathop{lim }},{f}’left( x right)<0$ nên ta chọn $k=-1$).
Khi đó $y=fleft( {{x}^{2}}-2 right)Rightarrow {y}’=-2x.{{x}^{2}}left( {{x}^{2}}-2 right)left( {{x}^{2}}-4 right)0Leftrightarrow left[ begin{array} {} x>2 \ {} 0<x<sqrt{2} \ {} -2<x<-sqrt{2} \ end{array} right.$.
Vậy hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() . Chọn B.
. Chọn B.
| Bài tập 4: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới đây:
Hàm số $y=fleft( 3-x right)$ đồng biến trên khoảng nào dưới đây? A. $left( -infty ;0 right)$. B. $left( 4;6 right)$. C. $left( -1;5 right)$. D. $left( 0;4 right)$. |
Lời giải
Dựa vào bảng xét dấu ta giả sử ${f}’left( x right)=left( x+1 right)left( x-3 right)$.
Khi đó $y=fleft( 3-x right)Rightarrow {y}’=-left( 3-x+1 right)left( 3-x-3 right)=-left( 4-x right)left( -x right)>0Leftrightarrow xleft( x-4 right)<0Leftrightarrow 0<x<4$.
Do đó hàm số $y=fleft( 3-x right)$ đồng biến trên khoảng $left( 0;4 right)$. Chọn D.
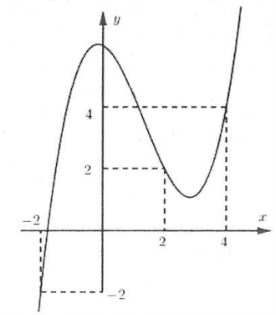
| Bài tập 5: Cho hàm số $y=fleft( x right)$. Biết rằng hàm số $y={f}’left( x right)$ có đồ thị như hình bên.
Hỏi hàm số $y=fleft( 3-{{x}^{2}} right)$ đồng biến trên khoảng nào sau đây?
A. $left( 0;1 right)$. B. $left( -1;0 right)$. C. $left( 2;3 right)$. D. $left( -2;-1 right)$. |
Lời giải
Giả sử ${f}’left( x right)=left( x+6 right)left( x+1 right)left( x-2 right)$, ta có: $y=fleft( 3-{{x}^{2}} right)Rightarrow {y}’=-2x.{f}’left( 3-{{x}^{2}} right)$.
$=-2x.left( 3-{{x}^{2}}+6 right)left( 3-{{x}^{2}}+1 right)left( 3-{{x}^{2}}-2 right)=2xleft( {{x}^{2}}-9 right)left( {{x}^{2}}-4 right)left( {{x}^{2}}-1 right)$
Bảng xét dấu cho ${y}’$:
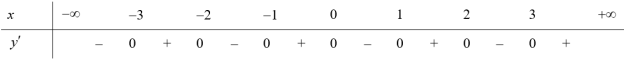
Do đó hàm số đồng biến trên khoảng $left( -1;0 right)$. Chọn B.
| Bài tập 6: Cho hàm số $y=fleft( x right)$. Biết rằng hàm số $y={f}’left( x right)$ có đồ thị như hình bên.
Hàm số $gleft( x right)=fleft( 1-2x right)$ đồng biến trên khoảng nào sau đây? A. $left( -1;0 right)$. B. $left( -infty ;0 right)$. C. $left( 0;1 right)$. D. $left( 1;+infty right)$. |
Lời giải
Giả sử ${f}’left( x right)=left( x+1 right)left( x-1 right)left( x-2 right){{left( x-4 right)}^{2}}$
Suy ra ${g}’left( x right)={f}’left( 1-2x right).{{left( 1-2x right)}^{prime }}=left( 2-2x right)left( -2x right)left( -1-2x right){{left( -3-2x right)}^{2}}.left( -2 right)>0$
$Leftrightarrow left( x-1 right)xleft( 2x+1 right)>0Leftrightarrow left[ begin{array} {} x>1 \ {} -frac{1}{2}<x<1 \ end{array} right.Rightarrow $ hàm số $gleft( x right)=fleft( 1-2x right)$ đồng biến trên khoảng $left( 1;+infty right)$.
Chọn D.
| Bài tập 7: Cho hàm số $y=fleft( x right)$. Biết rằng hàm số $y={f}’left( x right)$ có đồ thị như hình bên.
Hàm số $gleft( x right)=fleft( 3-2x right)$ nghịch biến trên khoảng nào sau đây? A. $left( 0;2 right)$. B. $left( 1;3 right)$. C. $left( -infty ;-1 right)$. D. $left( -1;+infty right)$. |
Lời giải
Giả sử ${f}’left( x right)=left( x+2 right)left( x-2 right)left( x-5 right)$
Ta có ${g}’left( x right)={f}’left( 3-2x right).{{left( 3-2x right)}^{prime }}=left( 5-2x right)left( 1-2x right)left( -2-2x right).left( -2 right)<0$.
$Leftrightarrow left( 2x-5 right)left( 2x-1 right)left( x+1 right)<0Leftrightarrow left[ begin{array} {} x<-1 \ {} frac{1}{2}<x<frac{5}{2} \ end{array} right.Rightarrow $ hàm số nghịch biến trên khoảng $left( -infty ;-1 right)$. Chọn C.
Bài tập 8: Cho hàm số $y={f}’left( x right)$ liên tục trên $mathbb{R}$ có đồ thị như hình bên. 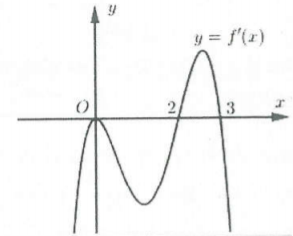
Hàm số $y=fleft( {{x}^{2}}-2x+3 right)$ nghịch biến trên khoảng nào sau đây? A. $left( -infty ;0 right)$. B. $left( 2;+infty right)$. C. $left( 1;2 right)$. D. $left( -infty ;2 right)$. |
Lời giải
Giả sử ${f}’left( x right)=-{{x}^{2}}left( x-2 right)left( x-3 right)$
Ta có ${{left[ fleft( {{x}^{2}}-2x+3 right) right]}^{prime }}=left( 2x-2 right).{f}’left( {{x}^{2}}-2x+3 right)$.
$Leftrightarrow -left( 2x-2 right){{left( {{x}^{2}}-2x+3 right)}^{2}}.left( {{x}^{2}}-2x+1 right).left( {{x}^{2}}-2x right)<0Leftrightarrow left( 2x-2 right)xleft( x-2 right)2 \ {} 0<x<1 \ end{array} right.$.
Do đó hàm số $y=fleft( {{x}^{2}}-2x+3 right)$ nghịch biến trên khoảng $left( 2;+infty right)$. Chọn B.
| Bài tập 9: Cho hàm số $y={f}’left( x right)$ liên tục trên $mathbb{R}$ có đồ thị như hình bên.
Hàm số $gleft( x right)=2fleft( x right)-{{x}^{2}}+4x-2$ đồng biến trên khoảng nào sau đây? A. $left( -infty ;-1 right)$, $left( 1;2 right)$. B. $left( -1;1 right)$, $left( 2;+infty right)$. C. $left( -1;2 right)$. D. $left( -infty ;-1 right)$,$left( 2;+infty right)$. |
Lời giải
Ta có: ${g}’left( x right)=2{f}’left( x right)-2x+4>0Leftrightarrow {f}’left( x right)>x-2$.
Vẽ đồ thị hàm số $y={f}’left( x right)$ và $y=x-2$ trên cùng hệ trục tọa độ Oxy, ta thấy với $x>2$ hoặc $-1<x<1$ thì đồ thị hàm số $y={f}’left( x right)$ nằm trên đường thẳng $y=x-2$.
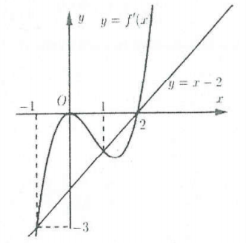
Vậy nên ${f}’left( x right)>x-2Leftrightarrow left[ begin{array} {} x>2 \ {} -1<x<1 \ end{array} right.$.
Do đó hàm số ![]() đồng biến trên các khoảng
đồng biến trên các khoảng ![]() ,
, ![]() .Chọn B.
.Chọn B.
| Bài tập 10: [Đề thi minh họa Bộ GD{}ĐT năm 2019] Cho hàm số $fleft( x right)$ có bảng xét dấu của đạo hàm như sau:
Hàm số $y=3fleft( x+2 right)-{{x}^{3}}+3x$ đồng biến trên khoảng nào dưới đây? A. $left( 1;+infty right)$. B. $left( -infty ;-1 right)$. C. $left( -1;0 right)$. D. $left( 0;2 right)$. |
Lời giải
Ta có: ${y}’=3{f}’left( x+2 right)-3{{x}^{2}}+3;text{ }{y}’=0Leftrightarrow {f}’left( x+2 right)={{x}^{2}}-1left( * right)$
Đặt $t=x+2$, khi đó $left( * right)Leftrightarrow {f}’left( t right)={{left( t-2 right)}^{2}}-1={{t}^{2}}-4t+3$
Dựa vào bảng biến thiên, ta thấy $tin left( 1;2 right)xrightarrow{{}}{f}’left( t right)>0$
Và ${{t}^{2}}-4t+3{{t}^{2}}-4t+3Leftrightarrow 1<t0Leftrightarrow 1<x+2<2Leftrightarrow -1<x<0$. Vậy hàm số đồng biến trên $left( -1;0 right)$. Chọn C.
| Bài tập 11: Cho hàm số $y=fleft( x right)$ liên tục trên $mathbb{R}$, đạo hàm ${f}’left( x right)$ có bảng xét dấu như sau:
Hàm số $y=fleft( x+1 right)-frac{{{x}^{3}}}{3}+x$ nghịch biến trên khoảng nào dưới đây? A. $left( 2;3 right)$. B. $left( 1;2 right)$. C. $left( 3;4 right)$. D. $left( 0;1 right)$. |
Lời giải
Ta có: ${y}’={f}’left( x+1 right)-{{x}^{2}}+1$.
Đặt $t=x+1$, khi đó ${y}’={f}’left( t right)-{{left( t-1 right)}^{2}}+1={f}’left( t right)-{{t}^{2}}+2t$.
Để hàm số nghịch biến thì ${y}'<0$
Ta chọn t sao cho: $left{ begin{array} {} {f}’left( t right)<0 \ {} -{{t}^{2}}+2t<0 \ end{array} right.Leftrightarrow left{ begin{array} {} {f}’left( t right)2 \ {} t<0 \ end{array} right. \ end{array} right.Leftrightarrow tin left( 2;3 right)Rightarrow xin left( 1;2 right)$.
Vậy hàm số nghịch biến trên khoảng $left( 1;2 right)$.Chọn B.
| Bài tập 12: Cho hàm số $y=fleft( x right)$có đồ thị đạo hàm ${f}’left( x right)$ trên $mathbb{R}$ như hình bên dưới và hàm số $gleft( x right)=fleft( {{x}^{2}}+x+2 right)$.
Hàm số $gleft( x right)$ đồng biến trên khoảng nào sau đây? A. $left( -1;0 right)$. B. $left( 0;1 right)$. C. $left( -2;-frac{1}{2} right)$. D. $left( -4;-2 right)$. |
Lời giải
Giả sử ${f}’left( x right)=left( x+2 right)left( x-2 right)left( x+1 right)$
Khi đó ${g}’left( x right)={{left[ fleft( {{x}^{2}}+x+2 right) right]}^{prime }}={{left( {{x}^{2}}+x+2 right)}^{prime }}.{f}’left( {{x}^{2}}+x+2 right)$
$=left( 2x+1 right)left( {{x}^{2}}+x+4 right)left( {{x}^{2}}+x right)left( {{x}^{2}}+x+3 right)>0Leftrightarrow left( 2x+1 right)xleft( x+1 right)>0Leftrightarrow left[ begin{array} {} x>0 \ {} -1<x<-frac{1}{2} \ end{array} right.$.
Suy ra hàm số $gleft( x right)$ đồng biến trên khoảng $left( 0;1 right)$. Chọn B.
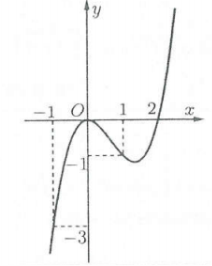
| Bài tập : Cho hàm số $y=fleft( x right)$có đồ thị đạo hàm ${f}’left( x right)$ như hình vẽ.
Xét hàm số $gleft( x right)=frac{1}{3}{{x}^{3}}+frac{3}{4}{{x}^{2}}-frac{3}{2}x-fleft( x right)$. Khẳng định nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng $left( -3;-1 right)$. B. Hàm số nghịch biến trên khoảng $left( 1;3 right)$. C. Hàm số nghịch biến trên khoảng $left( -1;0 right)$. D. Hàm số đồng biến trên khoảng $left( -2;0 right)$. |
Lời giải
Khẳng định 1 đúng. Ta có: ${g}’left( x right)=left( {{x}^{2}}+frac{3}{2}x-frac{3}{2} right)-{f}’left( x right)=0$
Parabol $y={{x}^{2}}+frac{3}{2}x-frac{3}{2}=hleft( x right)$ đi qua 3 điểm $left( -3;3 right),text{ }left( -1;2 right)$ và $left( 1;1 right)$.
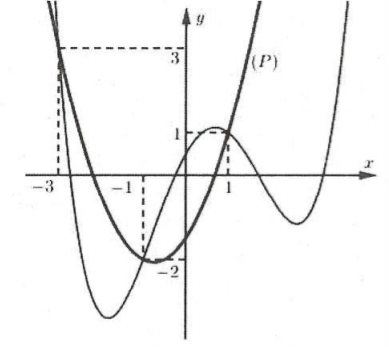
Dựa vào sự tương giao của hai đồ thị ta có: ${g}’left( x right)=hleft( x right)-{f}’left( x right)=0Leftrightarrow left[ begin{array} {} x=-3 \ {} x=-1 \ {} x=1 \ end{array} right.$ .
Khi $xto +infty $ thì ${f}’left( x right)0$ do đó ta có bảng xét dấu.
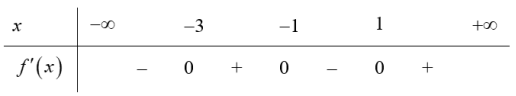
Dựa vào bảng xét dấu suy ra hàm số nghịch biến trên khoảng $left( -1;1 right)$ nên hàm số nghịch biến trên khoảng $left( -1;0 right)$. Chọn C.
| Bài tập 14: Cho hàm số $y=fleft( x right)$có đồ thị đạo hàm ${f}’left( x right)$ như hình vẽ.
Hàm số $gleft( x right)=fleft( x right)-frac{1}{3}{{x}^{3}}+2018$ nghịch biến trên khoảng nào sau đây. A. $left( -1;1 right)$. B. $left( -1;0 right)$. C. $left( 0;2 right)$. D. $left( -2;-1 right)$. |
Lời giải
Ta có: ${g}’left( x right)={f}’left( x right)-{{x}^{2}}$, parabol $y={{x}^{2}}$ cũng đi qua các điểm $left( -1;1 right),text{ }left( 0;0 right),text{ }left( 1;1 right)$ nằm trên đồ thị (Parabol $y={{x}^{2}}$ có đồ thị đậm hơn trong hình vẽ dưới).
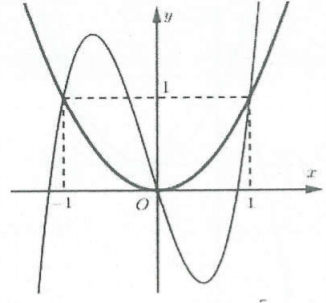
Dựa vào sự tương giao của hai đồ thị ta có ${f}’left( x right)-{{x}^{2}}=0Leftrightarrow left[ begin{array} {} x=-1 \ {} x=0 \ {} x=1 \ end{array} right.,xto -infty Rightarrow {f}’left( x right)<{{x}^{2}}$.
Từ đó, ta có bảng xét dấu cho ${g}’left( x right)$ như sau:

Do đó hàm số $gleft( x right)$ nghịch biến trên khoảng $left( -1;0 right)$.
| Bài tập 15: Cho hàm số $y=fleft( x right)$có đồ thị đạo hàm ${f}’left( x right)$ như hình vẽ.
Hàm số $gleft( x right)=fleft( x right)-frac{1}{3}{{x}^{3}}+{{x}^{2}}-x$ nghịch biến trên khoảng nào sau đây. A. $left( 0;1 right)$. B. $left( 1;2 right)$. C. $left( -1;1 right)$. D. $left( 2;+infty right)$. |
Lời giải
Ta có: ${g}’left( x right)={f}’left( x right)-{{x}^{2}}+2x-1=0Leftrightarrow {f}’left( x right)={{left( x-1 right)}^{2}}$.
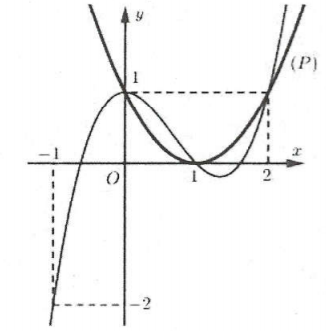
Dựa vào sự tương giao của đồ thị hàm số $y={f}’left( x right)$ và Parabol $y={{left( x-1 right)}^{2}}$ ta có:
${f}’left( x right)={{left( x-1 right)}^{2}}Leftrightarrow left[ begin{array} {} x=0 \ {} x=1 \ {} x=2 \ end{array} right.$. Từ đó ta có bảng xét dấu của ${g}’left( x right)$ như sau:
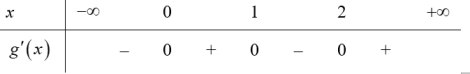
Do đó hàm số $gleft( x right)$ nghịch biến trên khoảng $left( 1;2 right)$. Chọn B.
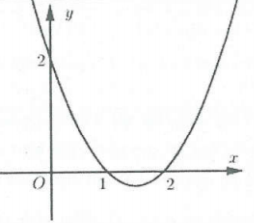
| Bài tập 16: Cho hàm số $y=fleft( x right)$ có đồ thị như hình vẽ
Hàm số $y=fleft( {{x}^{2}}-2x+1 right)+2018$ giảm trên khoảng A. $left( -infty ;1 right)$. B. $left( 2;+infty right)$. C. $left( 0;1 right)$. D. $left( 1;2 right)$. |
Lời giải
Dựa vào đồ thị hàm số $y=fleft( x right)Rightarrow {f}’left( x right)$ đổi dấu khi qua các điểm $x=-1;text{ }x=1$.
Giả sử ${f}’left( x right)=kleft( x+1 right)left( x-1 right),underset{xto +infty }{mathop{lim }},fleft( x right)>0Rightarrow k>0$ ta có:
$y=fleft( {{x}^{2}}-2x+1 right)+2018Rightarrow {y}’=left( 2x-2 right).{f}’left( {{x}^{2}}-2x+1 right)=kleft( 2x-2 right)left( {{x}^{2}}-2x+2 right)left( {{x}^{2}}-2x right)$
$=2kleft( x-1 right)xleft( x-2 right).left[ {{left( x-1 right)}^{2}}+1 right]<0Leftrightarrow xleft( x-1 right)left( x-2 right)<0Leftrightarrow left[ begin{array} {} 1<x<2 \ {} x<0 \ end{array} right.$.
Do đó hàm số giảm trên khoảng $left( 1;2 right)$. Chọn D.
| Bài tập 17: Cho hàm số $y=fleft( x right)$có đồ thị đạo hàm $y={f}’left( x right)$ như hình vẽ.
Hàm số $gleft( x right)=2fleft( x right)+{{left( x+1 right)}^{2}}$ đồng biến trên khoảng nào sau đây. A. $left( -3;1 right)$. B. $left( 1;3 right)$. C. $left( -infty ;3 right)$. D. $left( 3;+infty right)$. |
Lời giải
Ta có: ${g}’left( x right)=2{f}’left( x right)+2left( x+1 right)=2left[ {f}’left( x right)-left( -x-1 right) right]>0Leftrightarrow {f}’left( x right)>-x-1$.
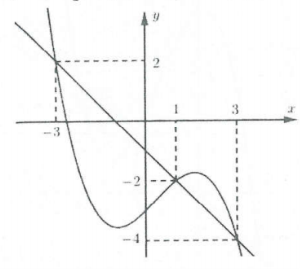
Dựa vào sự tương giao của đồ thị hàm số $y={f}’left( x right)$ và $y=-x-1$ ta có ${f}’left( x right)=-x-1Leftrightarrow left[ begin{array} {} x=-3 \ {} x=1 \ {} x=3 \ end{array} right.$.
Dễ thấy khi $xto +infty $ thì $-x-1>{f}’left( x right)Rightarrow {g}’left( x right)<0$ ta có bảng xét dấu ${g}’left( x right)$
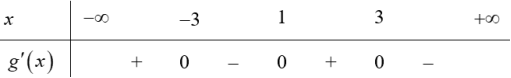
Hàm số $y=gleft( x right)$ đồng biến trên khoảng $left( -infty ;3 right)$ và $left( 1;3 right)$. Chọn B.
| Bài tập 18: Cho hàm số $y=fleft( x right)$có đồ thị đạo hàm $y={f}’left( x right)$ như hình vẽ. Đặt $hleft( x right)=2fleft( x right)-{{x}^{2}}$.
Hàm số $y=hleft( x right)$ đồng biến trên khoảng nào sau đây. A. $left( -infty ;-2 right)$. B. $left( 2;4 right)$. C. $left( -2;2 right)$. D. $left( 2;+infty right)$. |
Lời giải
Ta có: ${h}’left( x right)=2{f}’left( x right)-2x=2left[ {f}’left( x right)-x right]>0Leftrightarrow {f}’left( x right)>x$
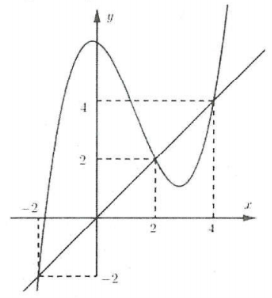
Dựa vào sự tương giao của đồ thị hàm số $y={f}’left( x right)$ và $y=x$ ta có ${f}’left( x right)=xLeftrightarrow left[ begin{array} {} x=-2 \ {} x=2 \ {} x=4 \ end{array} right.$.
Lập bảng xét dấu cho ${h}’left( x right)$

Dựa vào bảng xét dấu suy ra hàm số $y=hleft( x right)$ đồng biến trên khoảng $left( -2;2 right)$. Chọn C.
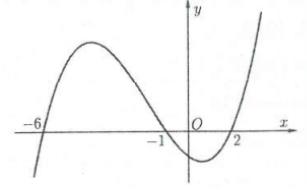
| Bài tập 19: Cho hàm số $y=fleft( x right)$có đồ thị đạo hàm $y={f}’left( x right)$là Parabol như hình vẽ bên.
Hàm số $y=fleft( 1-{{x}^{2}} right)+6{{x}^{2}}$ đồng biến trên khoảng nào sau đây? A. $left( -infty ;-1 right)$. B. $left( sqrt{2};+infty right)$. C. $left( -sqrt{2};0 right)$. D. $left( 1;sqrt{2} right)$. |
Lời giải
Giả sử ${f}’left( x right)=kleft( x-1 right)left( x-2 right)$, do ${f}’left( 0 right)=2Rightarrow k=1Rightarrow {f}’left( x right)=left( x-1 right)left( x-2 right)$.
Khi đó: $y=fleft( 1-{{x}^{2}} right)+6{{x}^{2}}Rightarrow {y}’=-2xleft( 1-{{x}^{2}}-1 right)left( 1-{{x}^{2}}-2 right)+12x$
$=-2xleft[ {{x}^{2}}left( {{x}^{2}}-1 right)-6 right]=-2xleft( {{x}^{2}}-3 right)left( {{x}^{2}}+2 right)$
Bảng xét dấu:

Do đó hàm số đồng biến trên khoảng $left( 0;sqrt{3} right)$ và $left( -infty ;-sqrt{3} right)$. Do đó hàm số đồng biến trên khoảng $left( 1;sqrt{2} right)$. Chọn D.
| Bài tập 20: Cho hàm số $y=fleft( x right)$. Hàm số $y={f}’left( x right)$ có bảng biến thiên như sau:
Bất phương trình $fleft( x right)>{{x}^{3}}-{{x}^{2}}-3x+m$ đúng với mọi $xin left( -1;1 right)$ khi và chỉ khi A. $m<fleft( -1 right)-1$. B. $m<fleft( -1 right)-1$. C. $mle fleft( 1 right)+3$. D. $m<fleft( 1 right)+3$. |
Lời giải
Bất phương trình $fleft( x right)>{{x}^{3}}-{{x}^{2}}-3x+mLeftrightarrow fleft( x right)-left( {{x}^{3}}-{{x}^{2}}-3x right)>mtext{ }left( forall xin left( -1;1 right) right)$.
Xét $gleft( x right)=fleft( x right)-left( {{x}^{3}}-{{x}^{2}}-3x right)Rightarrow {g}’left( x right)={f}’left( x right)-left( 3{{x}^{2}}-2x-3 right)$
Do Parabol $y=3{{x}^{2}}-2x-3$ đi qua 2 điểm $left( -1;2 right)$ và $left( 1;-2 right)$ nên ta thấy
${f}’left( x right)ge 3{{x}^{2}}-2x-3text{ }left( forall xleft( -1;1 right) right)$ suy ra hàm số $gleft( x right)=fleft( x right)-left( {{x}^{3}}-{{x}^{2}}-3x right)$ đồng biến trên khoảng $left( -1;1 right)$ nên $gleft( x right)>gleft( -1 right)text{ }left( forall xleft( -1;1 right) right)$.
Suy ra $mle fleft( -1 right)-1$ là giá trị cần tìm. Chọn B.
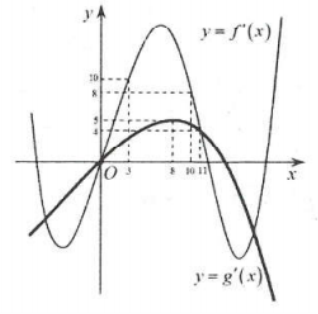
| Bài tập 21: [Đề thi THPT Quốc gia 2018] Cho hai hàm số $y=fleft( x right)$ và $y=gleft( x right)$. Hai hàm số $y={f}’left( x right)$ và $y={g}’left( x right)$ có đồ thị như hình vẽ dưới đây, trong đó đường cong đậm hơn là đồ thị hàm số $y={g}’left( x right)$.
Hàm số $hleft( x right)=fleft( x+6 right)-gleft( 2x+frac{5}{2} right)$ đồng biến trên khoảng nào dưới đây? A. $left( frac{21}{5};+infty right)$. B. $left( frac{1}{4};1 right)$. C. $left( 3;frac{21}{5} right)$. D. $left( 4;frac{17}{4} right)$. |
Lời giải
Ta có: ${h}’left( x right)={f}’left( x+6 right)-2{g}’left( 2x+frac{5}{2} right)>0$
Trên đoạn $left[ 3;8 right]$, ta được $underset{left[ 3;8 right]}{mathop{min }},{f}’left( x right)=fleft( 3 right)=10;underset{left[ 3;8 right]}{mathop{max }},{g}’left( x right)=gleft( 8 right)=5$.
Do đó ${f}’left( x right)-2{g}’left( x right)>0Leftrightarrow {f}’left( x right)>2{g}’left( x right);forall xin left( 3;8 right)$
Nếu $left{ begin{array} {} 3<x+6<8 \ {} 3<2x+frac{5}{2}<8 \ end{array} right.Rightarrow frac{1}{4}<x2{g}’left( 2x+frac{5}{2} right)Rightarrow {h}’left( x right)>0$ trên khoảng $left( frac{1}{4};2 right)$.
Vậy hàm số đã cho đồng biến trên khoảng $left( frac{1}{4};2 right)$. Chọn B.
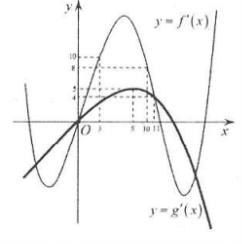
| Bài tập 22: [Đề thi THPT Quốc gia 2018] Cho hai hàm số $y=fleft( x right)$ và $y=gleft( x right)$. Hai hàm số $y={f}’left( x right)$ và $y={g}’left( x right)$ có đồ thị như hình vẽ dưới đây, trong đó đường cong đậm hơn là đồ thị hàm số $y={g}’left( x right)$.
Hàm số $hleft( x right)=fleft( x+3 right)-gleft( 2x-frac{7}{2} right)$ đồng biến trên khoảng nào dưới đây? A. $left( frac{13}{4};4 right)$. B. $left( 7;frac{29}{4} right)$. C. $left( 6;frac{36}{5} right)$. D. $left( frac{36}{5};+infty right)$ |
Lời giải
Ta có: ${h}’left( x right)={f}’left( x+3 right)-2{g}’left( 2x-frac{7}{2} right)>0$
Trên đoạn $left[ 3;8 right]$, ta được $underset{left[ 3;8 right]}{mathop{min }},{f}’left( x right)=fleft( 3 right)=10;underset{left[ 3;8 right]}{mathop{max }},{g}’left( x right)=gleft( 8 right)=5$.
Do đó ${f}’left( x right)-2{g}’left( x right)>0Leftrightarrow {f}’left( x right)>2{g}’left( x right);forall xin left( 3;8 right)$
Nếu $left{ begin{array} {} 3<x+3<8 \ {} 3<2x-frac{7}{2}<8 \ end{array} right.Rightarrow frac{13}{4}<x2{g}’left( 2x-frac{7}{2} right)Rightarrow {h}’left( x right)>0$ trên khoảng $left( frac{13}{4};5 right)$.
.Vậy hàm số đã cho đồng biến trên khoảng $left( frac{13}{4};4 right)$. Chọn A.