Bài tập tính Thể tích khối lăng trụ xiên có đáp án chi tiết
Một số bài tập trắc nghiệm tính thể tích khối lăng trụ xiên có Lời giải chi tiết
| Bài tập 1: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác vuông cân $AC=BC=3a$, hình chiếu vuông góc của ${B}’$lên mặt đáy trùng với trọng tâm tam giác ABC, mặt phẳng $left( AB{B}'{A}’ right)$ tạo với mặt phẳng $left( ABC right)$ một góc $60{}^circ $. Thể tích khối lăng trụ đã cho là:
A. $frac{9{{a}^{3}}sqrt{6}}{8}$ B. $frac{9{{a}^{3}}sqrt{6}}{4}$ C. $frac{3{{a}^{3}}sqrt{6}}{4}$ D. $frac{9{{a}^{3}}}{4}$ |
Lời giải chi tiết

Dựng $CIbot ABRightarrow I$ là trung điểm của AB.
Ta có: $left( {B}’GI right)bot ABRightarrow widehat{{B}’IG,}=60{}^circ .$
Lại có: $CI=frac{1}{2}AB=frac{3asqrt{2}}{2}Rightarrow GI=frac{asqrt{2}}{2}$
$Rightarrow {B}’G=GItan 60{}^circ =frac{asqrt{6}}{2}$
${{V}_{ABC.{A}'{B}'{C}’}}={B}’G.{{S}_{ABC}}=frac{asqrt{6}}{2}.frac{9{{a}^{2}}}{2}=frac{9{{a}^{3}}sqrt{6}}{4}$.Chọn B.
| Bài tập 2: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh a, hình chiếu vuông góc của ${B}’$ lên mặt phẳng đáy trùng với trung điểm H của cạnh AB, góc giữa mặt phẳng $left( BC{C}'{B}’ right)$ và mặt phẳng đáy bằng $60{}^circ $. Thể tích khối lăng trụ đã cho là:
A. $frac{3{{a}^{3}}sqrt{3}}{8}$ B. $frac{9{{a}^{3}}sqrt{3}}{16}$ C. $frac{3{{a}^{3}}sqrt{6}}{16}$ D. $frac{3{{a}^{3}}sqrt{3}}{16}$ |
Lời giải chi tiết

Kẻ $HKbot BCRightarrow BCbot left( {B}’HK right)Rightarrow widehat{{B}’KH}=60{}^circ .$
Ta có: $HK=HBsin 60{}^circ =frac{asqrt{3}}{4}Rightarrow {B}’H=HKtan 60{}^circ =frac{3a}{4}$
${{V}_{ABC.{A}'{B}'{C}’}}={B}’H.{{S}_{ABC}}=frac{3a}{4}.frac{{{a}^{2}}sqrt{3}}{4}=frac{3{{a}^{3}}sqrt{3}}{16}$.
Chọn D.
| Bài tập 3: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của ${A}’$trên mặt phẳng $left( ABC right)$ là trùng với trọng tâm tam giác ABC, góc giữa đường thẳng $A{A}’$ và mặt phẳng đáy $left( ABC right)$ bằng $30{}^circ $. Thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$ là:
A. $frac{{{a}^{3}}sqrt{3}}{4}$ B. $frac{{{a}^{3}}sqrt{3}}{16}$ C. $frac{5{{a}^{3}}sqrt{3}}{12}$ D. $frac{{{a}^{3}}sqrt{3}}{12}$ |
Lời giải chi tiết

Gọi H là trọng tâm tam giác đều ABC và M là trung điểm của BC.
Ta có: $AM=frac{asqrt{3}}{2}Rightarrow AH=frac{2}{3}AM=frac{asqrt{3}}{3}$
Khi đó: ${A}’H=HAtan 30{}^circ =frac{a}{3},{{S}_{ABC}}=frac{{{a}^{2}}sqrt{3}}{4}$
Do vậy: ${{V}_{ABC.{A}'{B}'{C}’}}={{S}_{ABC}}.{A}’H=frac{{{a}^{3}}sqrt{3}}{12}$
Chọn D.
| Bài tập 4: Cho lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh 4a. Hình chiếu của ${A}’$ trên mặt phẳng $left( ABC right)$ là điểm H thuộc cạnh AB sao cho $HB=3HA.$ Góc tạo bởi đường thẳng ${A}’C$ và mặt đáy bằng $30{}^circ $. Thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$ là:
A. $4{{a}^{3}}sqrt{13}$ B. $frac{{{a}^{3}}sqrt{13}}{8}$ C. $frac{{{a}^{3}}sqrt{13}}{4}$ D. ${{a}^{3}}sqrt{13}$ |
Lời giải chi tiết
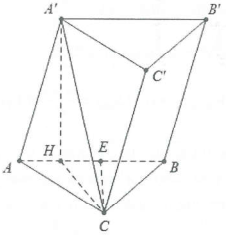
Ta có: $HB=3a;HA=a.$Gọi E là trung điểm của AB.
Ta có: $CE=frac{left( 4a right)sqrt{3}}{2}=2asqrt{3}$
$Rightarrow C{{H}^{2}}=H{{A}^{2}}+A{{C}^{2}}-2HA.ACcos 60{}^circ =13{{a}^{2}}$
Hoặc $CH=sqrt{C{{E}^{2}}+H{{E}^{2}}}=asqrt{13}$
$Rightarrow {A}’H=CHtan 30{}^circ =frac{asqrt{13}}{sqrt{3}};{{S}_{ABC}}=4{{a}^{2}}sqrt{3}$
Khi đó ${{V}_{ABC.{A}'{B}'{C}’}}={{S}_{ABC}}.{A}’H=4{{a}^{3}}sqrt{13}$
Chọn A.
| Bài tập 5: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy ABC là tam giác vuông cân tại C có $AC=BC=2a,$hình chiếu vuông góc của ${A}’$lên mặt đáy trùng với trung điểm của AB. Biết khoảng cách giữa 2 đường thẳng ${A}’C$và AB bằng $frac{2a}{sqrt{3}}.$ Thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$ là:
A. $4{{a}^{3}}sqrt{2}$ B. $8{{a}^{3}}$ C. $4{{a}^{3}}$ D. $2{{a}^{3}}$ |
Lời giải chi tiết

Gọi H là trung điểm của $ABRightarrow CH=asqrt{2}$
Khi đó ta có: $left{ begin{matrix} CHbot AB \ ABbot {A}’H \end{matrix} right.Rightarrow ABbot left( {A}’HC right)$
Dựng $HKbot {A}’CRightarrow dleft( {A}’C;AB right)=HK$
Mặt khác $frac{1}{HK}=frac{1}{A{{H}^{2}}}+frac{1}{H{{C}^{2}}}Rightarrow {A}’H=2a$
Do vậy ${{V}_{ABC.{A}'{B}'{C}’}}={A}’H.{{S}_{ABC}}=4{{a}^{3}}$. Chọn C.
| Bài tập 6: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh a. Gọi M là trung điểm của AB, tam giác ${C}’MC$ cân tại ${C}’$ và thuộc mặt phẳng vuông góc với đáy. Đường thẳng $A{C}’$ tạo với đáy góc $60{}^circ $. Thể tích khối lăng trụ là:
A. $frac{3{{a}^{3}}sqrt{7}}{16}$ B. $frac{{{a}^{3}}sqrt{21}}{16}$ C. $frac{3{{a}^{3}}sqrt{3}}{16}$ D. $frac{{{a}^{3}}sqrt{21}}{4}$ |
Lời giải chi tiết

Ta có: $CM=frac{asqrt{3}}{2},{{S}_{ABC}}=frac{{{a}^{2}}sqrt{3}}{4}$
Gọi H là trung điểm của CM suy ra ${C}’Hbot CM.$
Mặt khác có $left( {C}’MC right)bot left( ABC right)Rightarrow {C}’Hbot left( ABC right)$
$Rightarrow widehat{left( A{C}’;left( ABC right) right)}=widehat{{C}’AH}=60{}^circ ..$
Lại có $AH=sqrt{M{{H}^{2}}+A{{M}^{2}}}=frac{asqrt{7}}{4}.$
Suy ra ${C}’H=AHtan 60{}^circ =frac{asqrt{21}}{4}$.
Vậy ${{V}_{ABC.{A}'{B}'{C}’}}={C}’H.{{S}_{ABC}}=frac{3{{a}^{3}}sqrt{7}}{16}$. Chọn A.
| Bài tập 7: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có tam giác ABC vuông tại B, có $AB=a,AC=2a$. Tam giác ${A}’AC$ cân tại ${A}’$ và thuộc mặt phẳng vuông góc với đáy. Mặt phẳng $left( {A}’AC right)$ tạo với đáy một góc $45{}^circ $. Thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$ là:
A. $2{{a}^{3}}sqrt{3}$ B. $frac{{{a}^{3}}sqrt{3}}{12}$ C. $frac{{{a}^{3}}sqrt{3}}{6}$ D. $frac{{{a}^{3}}sqrt{3}}{4}$ |
Lời giải chi tiết

Gọi H là trung điểm của AC khi đó $AHbot AC$.
Mặt khác $left( {A}’AC right)bot left( ABC right).$
Do đó ${A}’Hbot left( ABC right)$. Dựng $HKbot BC$
$Rightarrow left( {A}’HK right)bot BCRightarrow widehat{{A}’KH}=45{}^circ $
Ta có: $HK=frac{AB}{2}=frac{a}{2}Rightarrow {A}’H=HK=frac{a}{2}$
${{V}_{ABC.{A}'{B}'{C}’}}={A}’H.{{S}_{ABC}}=frac{a}{2}.frac{{{a}^{2}}sqrt{3}}{2}=frac{{{a}^{3}}sqrt{3}}{4}$
Chọn D.
| Bài tập 8: Cho khối lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác ABC vuông tại B có $AB=BC=2a$. Biết rằng hình chiếu của ${A}’$ lên mặt đáy trùng với trọng tâm tam giác ABC. Biết ${A}’C=frac{2asqrt{14}}{3}$. Thể tích khối lăng trụ đã cho là:
A. $2{{a}^{3}}$ B. $4{{a}^{3}}$ C. $frac{4{{a}^{3}}}{3}$ D. $8{{a}^{3}}$ |
Lời giải chi tiết

Gọi H là trọng tâm tam giác ABC. Gọi M là trung điểm của AB ta có: $CM=sqrt{M{{B}^{2}}+C{{B}^{2}}}=asqrt{5}$
$Rightarrow CH=frac{2}{3}asqrt{5}Rightarrow {A}’H=sqrt{{A}'{{C}^{2}}-C{{H}^{2}}}=2a$
Do vậy ${{V}_{ABC.{A}'{B}'{C}’}}={A}’H.{{S}_{ABC}}=2a.frac{{{left( 2a right)}^{2}}}{2}=4{{a}^{3}}$.
Chọn B.
| Bài tập 9: Cho khối lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác ABC đều cạnh 6a. Hình chiếu vuông góc của đỉnh ${A}’$ xuống mặt đáy thuộc cạnh AC sao cho $HC=2HA$. Biết khoảng cách từ C đến mặt phẳng $left( AB{B}'{A}’ right)$bằng $frac{9a}{2}$. Thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$ là:
A. $18{{a}^{3}}sqrt{3}$ B. $36{{a}^{3}}sqrt{3}$ C. $54{{a}^{3}}sqrt{3}$ D. $27{{a}^{3}}sqrt{3}$ |
Lời giải chi tiết

Dựng $HKbot AC,HFbot {A}’ERightarrow HFbot left( AB{A}’ right)$
Ta có: $dleft( C;left( AB{A}’ right) right)=3dleft( H;left( AB{A}’ right) right)=3HF=frac{9a}{2}$
Lại có: $HE=HAsin 60{}^circ =2asin 60{}^circ =asqrt{3};HF=frac{3a}{2}.$
Mặt khác: $frac{1}{H{{E}^{2}}}+frac{1}{{A}'{{H}^{2}}}=frac{1}{H{{F}^{2}}}Rightarrow {A}’H=3a.$
Vậy ${{V}_{ABC.{A}'{B}'{C}’}}={A}’H.{{S}_{ABC}}=3a.frac{{{left( 6a right)}^{2}}sqrt{3}}{4}=27{{a}^{3}}sqrt{3}$
Chọn D.
| Bài tập 10: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có đáy là tam giác đều cạnh a. Biết rằng hình chiếu vuông góc ${A}’$ xuống đáy trùng với trung điểm của AB và $A{C}’=frac{3a}{2}$. Thể tích khối lăng trụ đã cho là:
A. $frac{{{a}^{3}}}{4}$ B. $frac{{{a}^{3}}}{12}$ C. $frac{{{a}^{3}}sqrt{3}}{4}$ D. $frac{{{a}^{3}}sqrt{3}}{12}$ |
Lời giải chi tiết

Gọi H là trung điểm của $ABRightarrow AH=frac{a}{2}.$
Ta có: $ABbot {A}’H;ABbot CHRightarrow {C}’Hbot AB$
$Rightarrow A{{H}^{2}}+H{{{C}’}^{2}}=A{{{C}’}^{2}}Rightarrow H{{{C}’}^{2}}=A{{{C}’}^{2}}-A{{H}^{2}}=2{{a}^{2}}$
$Rightarrow {A}’H=sqrt{H{{{{C}’}}^{2}}-A{{{{C}’}}^{2}}}=a$
${{V}_{ABC.{A}'{B}'{C}’}}={A}’H.{{S}_{ABC}}=a.frac{{{a}^{2}}sqrt{3}}{4}=frac{{{a}^{3}}sqrt{3}}{4}$. Chọn C.
| Bài tập 11: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ biết ${C}’.ABC$là hình chóp tam giác đều có đường cao bằng h. Đường thẳng $A{A}’$tạo với đáy một góc $60{}^circ $. Thể tích khối lăng trụ đã cho tính theo h là:
A. $frac{{{h}^{3}}sqrt{3}}{8}$ B. $frac{{{h}^{3}}sqrt{3}}{4}$ C. $frac{3{{h}^{3}}}{4}$ D. $frac{{{h}^{3}}sqrt{3}}{2}$ |
Lời giải chi tiết

Gọi H là trọng tâm tam giác đều ABC.
Khi đó ${C}’Hbot left( ABC right)$ và ${C}’H=h.$
Ta có: $A{A}’//C{C}’$ suy ra $C{C}’$tạo với đáy một góc $60{}^circ $
$Rightarrow widehat{{C}’CH}=60{}^circ .$ Khi đó $CHtan 60{}^circ =hRightarrow CH=frac{h}{sqrt{3}}.$
Đặt $AB=aRightarrow CH=frac{2}{3}.frac{asqrt{3}}{2}=frac{asqrt{3}}{3}=frac{h}{sqrt{3}}Rightarrow h=a.$
Do đó ${{V}_{ABC.{A}'{B}'{C}’}}=frac{{{h}^{3}}sqrt{3}}{4}$. Chọn B.
| Bài tập 12: Cho hình lăng trụ $ABC.{A}'{B}'{C}’$có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của ${A}’$ xuống đáy là trung điểm của AB. Biết khoảng cách từ A đến mặt phẳng $left( {A}’BC right)$ bằng $frac{asqrt{15}}{5}$. Thể tích khối lăng trụ $ABC.{A}'{B}'{C}’$ là:
A. $frac{3{{a}^{3}}}{8}$ B. $frac{3{{a}^{3}}}{4}$ C. $frac{{{a}^{3}}}{8}$ D. $frac{{{a}^{3}}sqrt{3}}{8}$ |
Lời giải chi tiết

Gọi H là trung điểm của $ABRightarrow {A}’Hbot left( ABC right)$
Dựng $HEbot BC,HFbot {A}’E.$Khi đó $dleft( H;left( {A}’BC right) right)=HF.$
Mặt khác $HE=HBsin widehat{ABC}=frac{a}{2}sin 60{}^circ =frac{asqrt{3}}{4}.$
Lại có $dleft( A;left( {A}’BC right) right)=2dleft( H;left( {A}’BC right) right)=2HF=frac{asqrt{15}}{5}$
$Rightarrow HF=frac{asqrt{15}}{10}$. Mặt khác: $frac{1}{H{{F}^{2}}}=frac{1}{H{{E}^{2}}}+frac{1}{{A}'{{H}^{2}}}$
$Rightarrow {A}’H=frac{asqrt{3}}{2}Rightarrow V={A}’H.{{S}_{ABC}}=frac{3{{a}^{3}}}{8}$. Chọn A.
| Bài tập 13: Cho hình chóp hộp $ABCD.{A}'{B}'{C}'{D}’$ có đáy là hình chữ nhật có $AB=3a,AD=4a$
. Biết ${A}’A={A}’B={A}’C={A}’D$ và mặt phẳng $left( {A}’CD right)$ tạo với đáy một góc $60{}^circ$. Thể tích khối hộp đã cho là: A. $4{{a}^{3}}sqrt{3}$ B. $12{{a}^{3}}sqrt{3}$ C. $8{{a}^{3}}sqrt{3}$ D. $24{{a}^{3}}sqrt{3}$ |
Lời giải chi tiết
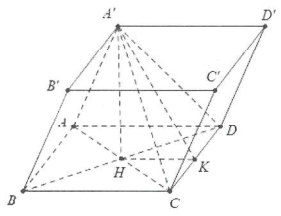
Ta có ${A}’A={A}’B={A}’C={A}’D$ nên hình chiếu của ${A}’$xuống mặt đáy trùng với tâm H của hình chữ nhật ABCD. Dựng $HKbot CD.$
Lại có ${A}’Hbot CDRightarrow CDbot left( {A}’CD right)$
Do vậy $widehat{left( left( {A}’CD right);left( ABCD right) right)}=widehat{{A}’KH}=60{}^circ .$
Lại có $HK=frac{AD}{2}=2Rightarrow {A}’H=HKtan 60{}^circ =2asqrt{3}$
Vậy ${{V}_{ABCD.{A}'{B}'{C}'{D}’}}={A}’H.{{S}_{ABCD}}=24{{a}^{3}}sqrt{3}$. Chọn D.
| Bài tập 14: Cho hình lăng trụ $ABCD.{A}'{B}'{C}'{D}’$ có đáy là hình thoi ABCD tâm O có $AC=2a,$$BD=2asqrt{3}.$ Hình chiếu vuông góc của ${B}’$ xuống đáy trùng cới trung điểm của OB. Đường thẳng ${B}’C$ tạo với đáy góc $45{}^circ $. Thể tích khối lăng trụ đã cho là:
A. $2{{a}^{3}}sqrt{7}.$ B. $2{{a}^{3}}sqrt{3}.$ C. $3{{a}^{3}}sqrt{21}.$ D. ${{a}^{3}}sqrt{21}.$ |
Lời giải chi tiết

Gọi H là trung điểm của OB. Khi đó
$OC=a,OH=frac{asqrt{3}}{2}Rightarrow CH=sqrt{O{{C}^{2}}+O{{H}^{2}}}=frac{asqrt{7}}{2}.$
Ta có: $widehat{left( {B}’C;left( ABC right) right)}=widehat{{B}’CH}=45{}^circ $
$Rightarrow {B}’H=CH=frac{asqrt{7}}{2}$
Lại có: ${{S}_{ABCD}}=frac{1}{2}AC.BD=2{{a}^{2}}sqrt{3}$
$Rightarrow {{V}_{ABCD.{A}'{B}'{C}'{D}’}}=2{{a}^{2}}sqrt{3}.frac{asqrt{7}}{2}={{a}^{3}}sqrt{21}.$ Chọn D
| Bài tập 15: Cho hình lăng trụ $ABCD.{A}'{B}'{C}'{D}’$ có đáy là hình vuông ABCD cạnh 6a. Hình chiếu vuông góc của ${A}’$xuống đáy trùng với trọng tâm tam giác ABD. Biết tam giác $A{A}’C$ vuông tại ${A}’$. Thể tích khối lăng trụ $ABCD.{A}'{B}'{C}'{D}’$ là:
A. $72{{a}^{3}}$ B. $144{{a}^{3}}$ C. $72{{a}^{3}}sqrt{3}$ D. $48{{a}^{3}}$ |
Lời giải chi tiết

Gọi G là trọng tâm tam giác ABD khi đó ta có:
$GA=frac{1}{3}AC$. Mặt khác $AC=6asqrt{2}.$
Suy ra $GA=2asqrt{2},GC=4asqrt{2}.$ Áp dụng hệ thức lượng trong tam giác $AC{A}’$ vuông tại ${A}’$có đường cao ${A}’G$ nên ta có: ${A}’G=sqrt{GA.GC}=4a$
$Rightarrow {{V}_{ABCD.{A}'{B}'{C}'{D}’}}={A}’G.{{S}_{ABCD}}=144{{a}^{3}}$. Chọn B.
| Bài tập 16: Cho lăng trụ $ABCD.{A}'{B}'{C}'{D}’$ có đáy ABCD là hình chữ nhật có $AB=2a,AD=2asqrt{3},$hình chiếu vuông góc của ${A}’$ lên mặt phẳng $left( ABCD right)$ trùng với tâm O của hình chữ nhật ABCD. Biết cạnh $A{A}’$ tạo với đáy một góc $60{}^circ $. Thể tích lăng trụ $ABCD.{A}'{B}'{C}'{D}’$ là:
A. $8{{a}^{3}}$ B. $12sqrt{3}{{a}^{3}}$ C. $24{{a}^{3}}$ D. $8sqrt{3}{{a}^{3}}$ |
Lời giải chi tiết

Ta có: $widehat{left( A{A}’;left( ABCD right) right)}=widehat{{A}’AO}=60{}^circ .$
Mặt khác: $AC=sqrt{A{{B}^{2}}+B{{C}^{2}}}=4aRightarrow OA=2a$
$Rightarrow O{A}’=OAtan 60{}^circ =2asqrt{3}$
${{V}_{ABCD.{A}'{B}'{C}'{D}’}}=O{A}’.{{S}_{ABCD}}=2asqrt{3}.4{{a}^{2}}sqrt{3}=24{{a}^{3}}$
Chọn C.
.
