CÁCH NHẬN DẠNG ĐỒ THỊ HÀM SỐ PHÂN THỨC $y=frac{ax+b}{cx+d}$ với $cne 0,,ad-bcne 0$
1. Đạo hàm hàm bậc nhất trên bậc nhất
Tập xác định $D=mathbb{R}backslash left{ -frac{d}{c} right}$
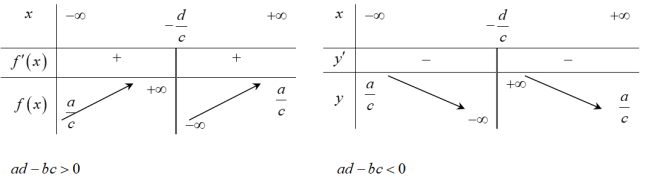
Đạo hàm ${y}’=frac{ad-bc}{cx+d},,,,forall xne -frac{d}{c}$ suy ra:
– Nếu $ad-bc>0to $ hàm số đồng biến trên mỗi khoảng xác định.
– Nếu $ad-bc<0to $ hàm số nghịch biến trên mỗi khoảng xác định.
2. Giới hạn, tiệm cận của hàm phân thức
– $underset{xto infty }{mathop{lim }},y=underset{xto infty }{mathop{lim }},frac{ax+b}{cx+d}=frac{a}{c}to y=frac{a}{c}$ là tiệm cận ngang của đồ thị hàm số
– $underset{xto -frac{d}{c}}{mathop{lim }},y=underset{xto -frac{d}{c}}{mathop{lim }},frac{ax+b}{cx+d}=infty to y=-frac{d}{c}$ là tiệm cận đứng của đồ thị hàm số
3. Bảng biến thiên hàm bậc nhất trên bậc nhất
4. Đồ thị hàm số phân thức
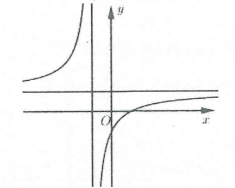
$ad-bc>0$ |
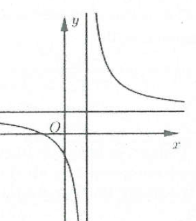
$ad-bc<0$ |
Đồ thị hàm số nhận $Ileft( -frac{d}{c};frac{a}{c} right)$ là giao điểm của hai đường tiệm cận làm tâm đối xứng.
5. Phương pháp giải toán
Để nhận diện hàm số phân thức bậc nhất: $y=frac{ax+b}{cx+d}$ $left( cne 0 right)$ ta làm như sau:
Dựa vào các đường tiệm cận đứng $x=-frac{d}{c}$ và tiệm cận ngang $y=frac{a}{c}$ .
Dựa vào giao điểm của đồ thị hàm số với trục hoành là điểm $left( frac{-b}{a};0 right)$ và giao điểm của đồ thị hàm số với trục tung là điểm $left( 0;frac{b}{d} right)$ .
Chú ý: Với các bài toán xác định dấu của $a,b,c,d$ ta có thể chọn $a>0$ (vì $y=frac{ax+b}{cx+d}=frac{-ax-b}{-cx-d}$) từ đó suy ra dấu của $b,c,d$.
