Xét tính đơn điệu của hàm số bậc 3 trên D có chứa tham số m
Phương pháp giải bài toán đơn điệu trên D của hàm bậc 3
þ Xét bài toán 2: Tìm điều kiện của tham số m để hàm số $y=fleft( x;m right)$ đồng biến hoặc nghịch biến trên D (trong đó D là một khoảng, đoạn hoặc nửa khoảng, nửa đoạn).
| Phương pháp giải:
Xét hàm số $fleft( x;m right)$ ta tính ${y}’={f}’left( x;m right)$. Hàm số đồng biến trên D ⇔ ${y}’ge 0text{ }left( forall xin D right)$. Hàm số nghịch biến trên D ⇔ ${y}’le 0text{ }left( forall xin D right)$. Cô lập tham số m và đưa bất phương trình ${y}’ge 0$ hoặc ${y}’le 0$ về dạng $mge fleft( x right)$ hoặc $mle fleft( x right)$. Sử dụng tính chất: § Bất phương trình: $mge fleft( x right)text{ }forall xin DLeftrightarrow mge underset{D}{mathop{Max}},fleft( x right)$. § Bất phương trình: $mle fleft( x right)text{ }forall xin DLeftrightarrow mle underset{D}{mathop{Min}},fleft( x right)$. |
Chú ý: Với hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+dtext{ }left( ane 0 right)$ liên tục trên $mathbb{R}$ nên hàm số đồng biến hoặc nghịch biến trên khoảng $left( a;b right)$ thì nó đồng biến trên đoạn $left[ a;b right]$.
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số các bạn xem chủ đề GTLN, GTNN của hàm số.
Lưu ý bất đẳng thức Cosi (AM – GM): Cho các số thực không âm ${{a}_{1}},text{ }{{a}_{2}},…,{{a}_{n}}$ thì ta có:
${{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}>nsqrt[n]{{{a}_{1}}{{a}_{2}}…{{a}_{n}}}$.
Dấu bằng xảy ra $Leftrightarrow {{a}_{1}}={{a}_{2}}=…={{a}_{n}}$.
Với hàm số lượng giác $Fleft( x right)=aoperatorname{sinx}+bcos x+c$ thì $left{ begin{array} {} MaxFleft( x right)=sqrt{{{a}^{2}}+{{b}^{2}}}+c \ {} MinFleft( x right)=-sqrt{{{a}^{2}}+{{b}^{2}}}+c \ end{array} right.$.
Bài tập xét tính đồng biến nghịch biến của hàm bậc 3 có đáp án
| Ví dụ 1: Tìm tất cả các giá trị thực của tham số m để hàm số $y={{x}^{3}}-3{{x}^{2}}+mx+1$ đồng biến trên khoảng $left( 0;+infty right)$. |
Lời giải chi tiết
Ta có: ${y}’=3{{x}^{2}}-6x+m$.
Hàm số đồng biến trên khoảng $left( 2;+infty right)$ $Leftrightarrow {y}’=3{{x}^{2}}-6x+mge 0text{ }forall xin left( 0;+infty right)$
$Leftrightarrow mge -3{{x}^{2}}+6x=gleft( x right)left( forall xin left( 0;+infty right) right)Leftrightarrow mge underset{left( 0;+infty right)}{mathop{max }},gleft( x right)$
Mặt khác ${g}’left( x right)=-6x+6=0Leftrightarrow x=1$. Ta có $underset{xto 0}{mathop{lim }},gleft( x right)=0;text{ }underset{xto +infty }{mathop{lim }},gleft( x right)=-infty ;text{ }gleft( 1 right)=3$.
Do vậy $underset{left( 0;+infty right)}{mathop{max }},gleft( x right)=+infty $. Do đó $mge 3$ là giá trị cần tìm.
| Ví dụ 2: Cho hàm số $y=-{{x}^{3}}+3{{x}^{2}}+3mx-1$. Xác định tất cả các giá trị của tham số m để hàm số đã cho nghịch biến trên khoảng $left( 0;+infty right)$. |
Lời giải chi tiết
Ta có: ${y}’=-3{{x}^{2}}+6x+3m$.
Hàm số đã cho nghịch biến trên khoảng $left( 0;+infty right)$ $Leftrightarrow {y}’le 0text{ }forall xsubset left( 0;+infty right)$
$Leftrightarrow mle {{x}^{2}}-2x=gleft( x right)text{ }forall xin left( 0;+infty right)Leftrightarrow mle underset{left( 0;+infty right)}{mathop{min }},gleft( x right)$
Xét $gleft( x right)={{x}^{2}}-2xleft( xin left( 0;+infty right) right)$ ta có: ${g}’left( x right)=2x-2=0Leftrightarrow x=1$
$underset{xto 0}{mathop{lim }},gleft( x right)=0;text{ }underset{xto +infty }{mathop{lim }},gleft( x right)=+infty ;text{ }gleft( 1 right)=-1$ nên $underset{left( 0;+infty right)}{mathop{min }},gleft( x right)=-1$
Do đó $mle -1$ là giá trị cần tìm.
| Ví dụ 3: Cho hàm số $y=frac{1}{3}{{x}^{3}}+{{x}^{2}}-mx+1$. Xác định tất cả các giá trị của tham số m để hàm số đã cho nghịch biến trên đoạn $left[ -2;0 right]$. |
Lời giải chi tiết
Ta có: ${y}’={{x}^{2}}+2x-m$.
Hàm số đã cho nghịch biến trên đoạn $left[ -2;0 right]$ $Leftrightarrow {y}’le 0text{ }left( forall xin left[ -2;0 right] right)$
$Leftrightarrow mge {{x}^{2}}+2x=gleft( x right)left( forall xin left[ -2;0 right] right)Leftrightarrow mge underset{left[ -2;0 right]}{mathop{max }},gleft( x right)$
Mặt khác ${g}’left( x right)=2x+2=0Leftrightarrow x=-1$
Lại có $gleft( -2 right)=0;text{ }gleft( 0 right)=0;text{ }gleft( -1 right)=-1$. Do vậy $underset{left[ -2;0 right]}{mathop{max }},gleft( x right)=0$
Vậy $mge 0$ là giá trị cần tìm.
| Ví dụ 4: [Đề thi tham khảo của Bộ GD{}ĐT năm 2019]: Tập hợp các giá trị thực của tham số m để hàm số $y=-{{x}^{3}}-6{{x}^{2}}+left( 4m-9 right)x+4$ nghịch biến trên khoảng $left( -infty ;-1 right)$ là
A. $left( -infty ;0 right]$. B. $left[ -frac{3}{4};+infty right)$. C. $left( -infty ;-frac{3}{4} right]$. D. $left[ 0;+infty right)$. |
Lời giải chi tiết
Ta có: ${y}’=-3{{x}^{2}}-12x+4m-9$.
Hàm số nghịch biến trên khoảng $left( -infty ;-1 right)$ $Leftrightarrow {y}’=-3{{x}^{2}}-12x+4m-9le 0text{ }left( forall xin left( -infty ;-1 right) right)$
$Leftrightarrow 4mle 3{{x}^{2}}+12x+9left( forall xin left( -infty ;-1 right) right)Leftrightarrow frac{4m}{3}le {{x}^{2}}+4x+3left( forall xin left( -infty ;-1 right) right)left( * right)$
Xét $gleft( x right)={{x}^{2}}+4x+3$ trên khoảng $left( -infty ;-1 right)$ ta có: ${g}’left( x right)=2x+4=0Leftrightarrow x=-2$.
Ta tìm được $underset{left( -infty ;-1 right)}{mathop{min }},gleft( x right)=gleft( -2 right)=-1Rightarrow left( * right)Leftrightarrow frac{4m}{3}le -1Leftrightarrow mle -frac{3}{4}$. Chọn C.
| Ví dụ 5: Tìm giá trị thực của tham số m để hàm số $y=frac{1}{3}{{x}^{3}}-left( m-2 right){{x}^{2}}+left( 2m+3 right)x$ nghịch biến trên khoảng $left( 0;3 right)$? |
Lời giải chi tiết
Ta có: ${y}’={{x}^{2}}+2left( m-2 right)x+2m+3$
Hàm số nghịch biến trên khoảng $left( 0;3 right)$ $Leftrightarrow {y}’le 0left( forall xin left[ 0;3 right] right)$ (Do hàm số liên tục trên $mathbb{R}$ nên ta mở rộng ra đoạn $left[ 0;3 right]$).
$Leftrightarrow {{x}^{2}}-4x+3le -2mleft( x+1 right)left( forall xin left[ 0;3 right] right)Leftrightarrow 2mle frac{-{{x}^{2}}+4x-3}{x+1}=gleft( x right)left( forall xin left[ 0;3 right] right)$
$Leftrightarrow 2mle underset{left[ 0;3 right]}{mathop{min }},gleft( x right)$
Ta có: ${g}’left( x right)=frac{-{{x}^{2}}-7x+7}{{{left( x+1 right)}^{2}}}=0xrightarrow{xin left[ 0;3 right]}x=-1+2sqrt{2}$
Mặt khác $gleft( 2sqrt{2}-1 right)=6-4sqrt{2},text{ }gleft( 0 right)=-3,text{ }gleft( 3 right)=0$.
Do đó $underset{left[ 0;3 right]}{mathop{min }},gleft( x right)=-3Rightarrow 2mle -3Leftrightarrow mle -frac{3}{2}$.
| Ví dụ 6: Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 20 để hàm số $y={{x}^{3}}+6{{x}^{2}}+left( m+2 right)x+{{m}^{2}}$ đồng biến trên khoảng $left( -1;+infty right)$.
A. 13. B. 14. C. 15. D. 16. |
Lời giải chi tiết
Ta có: ${y}’=3{{x}^{2}}+12x+m+2$
Hàm số đồng biến trên khoảng $left( -1;+infty right)Leftrightarrow {y}’ge 0left( forall xin left[ -1;+infty right) right)$ (Do hàm số đã cho liên tục trên $mathbb{R}$ nên ta có thể lấy $xin left[ -1;+infty right)$).
$Leftrightarrow gleft( x right)=3{{x}^{2}}+12x+2ge -mleft( forall xin left[ -1;+infty right) right)Leftrightarrow underset{left[ -1;+infty right)}{mathop{min }},gleft( x right)ge -mleft( * right)$
Ta có: ${g}’left( x right)=6x+12>0left( forall xin left[ -1;+infty right) right),text{ }gleft( -1 right)=-7$.
Suy ra $left( * right)Leftrightarrow -7ge -mLeftrightarrow mge 7$.
Kết hợp $left{ begin{array} {} m<20 \ {} min mathbb{Z} \
end{array} right.$ Þ có 13 giá trị của tham số m. Chọn A.
| Ví dụ 7: Tìm tham số m để hàm số sau đồng biến trên $left( 0;+infty right):y={{x}^{3}}+mx-frac{1}{3x}$.
A. $mle 1$ B. $mle 0$ C. $mge -1$ D. $mge -2$ |
Lời giải chi tiết
Ta có: ${y}’=3{{x}^{2}}+m+frac{1}{3{{x}^{2}}}$
Hàm số đồng biến trên $left( 0;+infty right)Leftrightarrow {y}’ge 0left( forall xin left( 0;+infty right) right)Leftrightarrow gleft( x right)=3{{x}^{2}}+frac{1}{3{{x}^{2}}}ge -mleft( forall xin left( 0;+infty right) right)$.
$Leftrightarrow underset{left( 0;+infty right)}{mathop{min }},gleft( x right)ge -mleft( * right)$.
Theo BĐT AM – GM ta có: $3{{x}^{2}}+frac{1}{3{{x}^{2}}}ge 2sqrt{3{{x}^{2}}.frac{1}{3{{x}^{2}}}}=2$
Do đó $left( * right)Leftrightarrow 2ge -mLeftrightarrow mge -2$. Chọn D.
| Ví dụ 8: Tập hợp các giá trị của –m để hàm số $y=-m{{x}^{3}}+{{x}^{2}}-3x+m-2$ nghịch biến trên $left( -3;0 right)$ là
A. $left[ -frac{1}{3};+infty right)$. B. $left( -frac{1}{3};+infty right)$. C. $left( -infty ;-frac{1}{3} right)$. D. $left[ -frac{1}{3};0 right)$. |
Lời giải chi tiết
Ta có: ${y}’={{left( -m{{x}^{3}}+{{x}^{2}}-3x+m-2 right)}^{prime }}=-3m{{x}^{2}}+2x-3$
Hàm số nghịch biến trên khoảng $left( -3;0 right)Leftrightarrow left{ begin{array} {} {y}’le 0 \ {} xin left( -3;0 right) \ end{array} right.Leftrightarrow left{ begin{array} {} -3m{{x}^{2}}+2x-3le 0 \ {} xin left( -3;0 right) \ end{array} right.Leftrightarrow left{ begin{array} {} mge frac{2x-3}{3{{x}^{2}}}=fleft( x right) \ {} xin left( -3;0 right) \ end{array} right.$
Ta có ${f}’left( x right)={{left( frac{2x-3}{3{{x}^{2}}} right)}^{prime }}=frac{2left( 3-x right)}{3{{x}^{3}}}>0left( forall xin left( -3;0 right) right)Rightarrow fleft( x right)$ đồng biến trên khoảng $left( -3;0 right)$.
Do đó $underset{left( -3;0 right)}{mathop{fleft( x right)}},<fleft( -3 right)=-frac{1}{3}left( forall xin left( -3;0 right) right)Rightarrow mge -frac{1}{3}Leftrightarrow min left[ -frac{1}{3};+infty right)$. Chọn A.
| Ví dụ 9: Biết rằng tập hợp tất cả các giá trị thực của tham số m để hàm số $y=frac{1}{3}{{x}^{3}}-left( m-1 right){{x}^{2}}-left( m-3 right)x+2017m$ đồng biến trên các khoảng $left( -3;-1 right)$ và $left( 0;3 right)$ là đoạn $T=left[ a;b right]$. Tính ${{a}^{2}}+{{b}^{2}}$.
A. ${{a}^{2}}+{{b}^{2}}=10$. B. ${{a}^{2}}+{{b}^{2}}=13$. C. ${{a}^{2}}+{{b}^{2}}=8$. D. ${{a}^{2}}+{{b}^{2}}=5$. |
Lời giải chi tiết
Ta có ${y}’={{x}^{2}}-2left( m-1 right)x-left( m-3 right)$
Để hàm số đồng biến trên các khoảng $left( -3;-1 right)$ và $left( 0;3 right)$ thì ${y}’ge 0$ với mọi $xin left( -3;-1 right)$ và $xin left( 0;3 right)$. Hay ${{x}^{2}}-2left( m-1 right)x-left( m-3 right)ge 0Leftrightarrow {{x}^{2}}+2x+3ge mleft( 2x+1 right)Leftrightarrow frac{{{x}^{2}}+2x+3}{2x+1}ge m$ với mọi $xin left( 0;3 right)$ và $frac{{{x}^{2}}+2x+3}{2x+1}le m$ với $xin left( -3;-1 right)$.
Xét ${f}’left( x right)={{left( frac{{{x}^{2}}+2x+3}{2x+1} right)}^{prime }}=frac{2left( x-1 right)left( x+2 right)}{{{left( 2x+1 right)}^{2}}}to {f}’left( x right)=0Leftrightarrow left[ begin{array} {} x=1 \ {} x=-2 \ end{array} right.$
Dựa vào bảng biến thiên của hàm số $fleft( x right)$, để $fleft( x right)$ đồng biến trên $left( 0;3 right)$ thì $mle 2$, để $fleft( x right)$ đồng biến trên $left( -3;-1 right)$ thì $mge -1Rightarrow min left[ -1;2 right]Rightarrow {{a}^{2}}+{{b}^{2}}=5$. Chọn D.
| Ví dụ 10: Để hàm số $y=-frac{{{x}^{3}}}{3}+left( a-1 right){{x}^{2}}+left( a+3 right)x-4$ đồng biến trên khoảng $left( 0;3 right)$ thì giá trị cần tìm của tham số a là
A. $a<-3$. B. $a>-3$. C. $-3<a<frac{12}{7}$. D. $age frac{12}{7}$. |
Lời giải chi tiết
Ta có: ${y}’=-{{x}^{2}}+2left( a-1 right)x+a+3$
Để hàm số đồng biến trên khoảng $left( 0;3 right)$ thì ${y}’ge 0text{ }left( forall xin left( 0;3 right) right)$
$Leftrightarrow -{{x}^{2}}+2left( a-1 right)x+a+3ge 0text{ }left( forall xin left( 0;3 right) right)$
$Leftrightarrow 2ax+age {{x}^{2}}+2x-3Leftrightarrow age frac{{{x}^{2}}+2x-3}{2x+1}Leftrightarrow age underset{left( 0;3 right)}{mathop{max }},fleft( x right)left( * right)$.
Xét hàm số $fleft( x right)=frac{{{x}^{2}}+2x-3}{2x+1}$ trên $left( 0;3 right)$.
Ta có: ${f}’left( x right)=frac{2{{x}^{2}}+2x+8}{{{left( 2x+1 right)}^{2}}}>0text{ }left( forall xin left( 0;3 right) right)Rightarrow fleft( x right)$ đồng biến trên khoảng $left( 0;3 right)$.
Vậy $fleft( x right)<fleft( 3 right)=frac{12}{7}$. Do đó $left( * right)Leftrightarrow age frac{12}{7}$. Chọn D.
| Ví dụ 11: Giá trị của tham số m sao cho hàm số $y={{x}^{3}}-2m{{x}^{2}}-left( m+1 right)x+1$ nghịch biến trên khoảng $left( 0;2 right)$ là
A. $mge -1$. B. $mle frac{11}{9}$. C. $mge frac{11}{9}$. D. $mle -1$. |
Lời giải chi tiết
Ta có: ${y}’=3{{x}^{2}}-4mx-m-1$
Hàm số nghịch biến biến trên khoảng $left( 0;2 right)Leftrightarrow 3{{x}^{2}}-4mx-m-1le 0text{ }left( forall xin left[ 0;2 right] right)$
$Leftrightarrow 3{{x}^{2}}-1le mleft( 4x+1 right)text{ }left( forall xin left( 0;2 right) right)Leftrightarrow frac{3{{x}^{2}}-1}{4x+1}le mleft( forall xin left[ 0;2 right] right)$.
Xét hàm số $gleft( x right)=frac{3{{x}^{2}}-1}{4x+1}text{ }left( xin left[ 0;2 right] right)$.
Ta có: ${g}’left( x right)=frac{6xleft( 4x+1 right)-4left( 3{{x}^{2}}-1 right)}{{{left( 4x+1 right)}^{2}}}=frac{12{{x}^{2}}+6x+4}{{{left( 4x+1 right)}^{2}}}>0left( forall xin left[ 0;2 right] right)$
$Rightarrow gleft( x right)$ đồng biến trên đoạn $left[ 0;2 right]$
Ta có: $gleft( x right)=frac{3{{x}^{2}}-1}{4x+1}le text{m }left( forall xin left[ 0;2 right] right)Leftrightarrow mge gleft( 2 right)=frac{11}{9}$. Chọn C.
| Ví dụ 12: Tìm tất cả các giá trị thực của tham số m để hàm số $y=2{{x}^{3}}-m{{x}^{2}}+2x$ đồng biến trên khoảng $left( -2;0 right)$.
A. $mge -2sqrt{3}$. B. $mle 2sqrt{3}$. C. $mge -frac{13}{2}$. D. $mge frac{13}{2}$. |
Lời giải chi tiết
Cách 1: Ta có: ${y}’=6{{x}^{2}}-2mx+2$
Hàm số đồng biến trên khoảng $left( -2;0 right)Leftrightarrow {y}’ge 0text{ }left( forall xin left( -2;0 right) right)$.
$Leftrightarrow mxle 3{{x}^{2}}+1text{ }left( forall xin left( -2;0 right) right)Leftrightarrow mge 3x+frac{1}{x}text{ }left( forall xin left( -2;0 right) right)Leftrightarrow mge underset{left( -2;0 right)}{mathop{max }},fleft( x right)$
Xét $fleft( x right)=3x+frac{1}{x}text{ }left( xin left( -2;0 right) right)$ ta có ${f}’left( x right)=3-frac{1}{{{x}^{2}}}=0Leftrightarrow left[ begin{array} {} x=frac{1}{sqrt{3}}text{ }left( loai right) \ {} x=-frac{1}{sqrt{3}} \ end{array} right.$
Lại có $underset{xto 0}{mathop{lim }},fleft( x right)=-infty ;underset{xto {{left( -2 right)}^{+}}}{mathop{lim }},fleft( x right)=frac{-13}{2},fleft( -frac{1}{sqrt{3}} right)=-2sqrt{3}$
Vậy $mge -2sqrt{3}$. Chọn A.
Cách 2: $fleft( x right)=3x+frac{1}{x}=-left[ 3left( -x right)+frac{1}{left( -x right)} right]le -2sqrt{3}Rightarrow underset{left( -2;0 right)}{mathop{max }},fleft( x right)=-2sqrt{3}$ khi $x=-frac{1}{sqrt{3}}$.
| Ví dụ 13: Có bao nhiêu giá trị nguyên âm của tham số m để hàm số $y={{x}^{3}}+mx-frac{1}{5{{x}^{5}}}$ đồng biến trên khoảng $left( 0;+infty right)$?
A. 5. B. 3. C. 0. D. 4. |
Lời giải chi tiết
Ta có: ${y}’=3{{x}^{2}}+m+frac{1}{{{x}^{6}}}$
Để hàm số đồng biến trên khoảng $left( 0;+infty right)Leftrightarrow {y}’ge 0text{ }left( forall xin left( 0;+infty right) right)$
$Leftrightarrow gleft( x right)=3{{x}^{2}}+frac{1}{{{x}^{6}}}ge -mtext{ }left( forall xin left( 0;+infty right) right)Leftrightarrow underset{left( 0;+infty right)}{mathop{min }},gleft( x right)ge -mleft( * right)$
Lại có: $gleft( x right)=3{{x}^{2}}+frac{1}{{{x}^{6}}}={{x}^{2}}+{{x}^{2}}+{{x}^{2}}+frac{1}{{{x}^{6}}}ge 4sqrt[4]{{{x}^{2}}.{{x}^{2}}.{{x}^{2}}.frac{1}{{{x}^{6}}}}=4$ (Bất đẳng thức AM – GM)
Do đó $left( * right)Leftrightarrow -mle 4Leftrightarrow mge -4$.
Theo bài ta có $min left{ -4;-3;-2;-1 right}$. Chọn D.
| Ví dụ 14: Tìm tất cả các giá trị thực của tham số m để hàm số $y={{x}^{4}}-2left( m-1 right){{x}^{2}}+m-2$ đồng biến trên khoảng $left( 1;3 right)$.
A. $mle 1$. B. $m<1$. C. $mle 2$. D. $m<2$. |
Lời giải chi tiết
Ta có: ${y}’=4{{x}^{3}}-4left( m-1 right)x$
Hàm số đồng biến trên khoảng $left( 1;3 right)Leftrightarrow 4{{x}^{3}}-4left( m-1 right)xge 0text{ }left( forall xin left[ 1;3 right] right)$ (Do hàm số đã cho liên tục trên $mathbb{R}$ nên ta có thể lấy x trên đoạn $left[ 1;3 right]$)
$Leftrightarrow gleft( x right)={{x}^{2}}ge m-1text{ }left( forall xin left[ 1;3 right] right)Leftrightarrow underset{left[ 1;3 right]}{mathop{min }},gleft( x right)ge m-1Leftrightarrow 1ge m-1Leftrightarrow mle 2$. Chọn C.
| Ví dụ 15: Tìm tất cả các giá trị thực của tham số m để hàm số $y={{x}^{4}}-{{m}^{2}}{{x}^{2}}+m$ đồng biến trên khoảng $left( 0;4 right)$.
A. $min left( -2;2 right)$. B. $min left( 0;2 right)$. C. $min varnothing $. D. $min left{ 0 right}$. |
Lời giải chi tiết
Ta có: ${y}’=4{{x}^{3}}-2{{m}^{2}}x$
Do hàm số đã cho liên tục trên $mathbb{R}$ nên nó đồng biến trên khoảng $left( 0;4 right)Leftrightarrow {y}’ge 0text{ }left( forall xin left[ 0;4 right] right)$
$Leftrightarrow 4{{x}^{3}}-2{{m}^{2}}xge 0text{ }left( forall xin left[ 0;4 right] right)Leftrightarrow 2{{x}^{2}}ge {{m}^{2}}text{ }left( forall xin left[ 0;4 right] right)Leftrightarrow {{m}^{2}}le 0Leftrightarrow m=0$. Chọn D.
| Ví dụ 16: Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=frac{2}{3}{{x}^{3}}-left( 2m-3 right){{x}^{2}}+2left( {{m}^{2}}-3m right)x+1$ nghịch biến trên khoảng $left( 1;3 right)$?
A. 4. B. 1. C. 2. D. 3. |
Lời giải chi tiết
Ta có: ${y}’=2{{x}^{2}}-2left( 2m-3 right)x+2left( {{m}^{2}}-3m right)=2left( x-m right)left[ x-left( m-3 right) right]<0Leftrightarrow m-3<x<m$
Hàm số nghịch biến trên khoảng $left( 1;3 right)Leftrightarrow m-3le 1le 3le mLeftrightarrow 3le mle 4$.
Vậy có 2 giá trị nguyên của tham số $m=left{ 3;4 right}$. Chọn C.
Lời giải
Ta có ${y}’={{x}^{2}}-left( 2m-1 right)x+{{m}^{2}}-m-2=left[ x-left( m-2 right) right]left[ x-left( m+1 right) right]$ .
Hàm số nghịch biến trên khoảng $left( 1;2 right)Leftrightarrow {y}’le 0,text{ }forall xin left( 1;2 right)Leftrightarrow left[ x-left( m-2 right) right]left[ x-left( m+1 right) right]le 0$.
$Leftrightarrow m-2le xle m+1$
Với $xin left( 1;2 right)Rightarrow left{ begin{array} {} xge 1Rightarrow m-2le 1Leftrightarrow mle 3 \ {} xle 2Rightarrow m+1ge 2Leftrightarrow mge 1 \ end{array} right.Rightarrow 1le mle 3$.
Suy ra có ba giá trị nguyên của m để hàm số nghịch biến trên khoảng![]() . Chọn D.
. Chọn D.
| Ví dụ 18: Tìm tất cả các giá trị của tham số m để hàm số $fleft( x right)=sqrt{{{x}^{2}}+4mx+4{{m}^{2}}+3}$ nghịch biến trên khoảng $left( -infty ;2 right)$.
A. $mle -1$. B. $m>-1$. C. $mle 2$. D. $m>2$. |
Lời giải
Hàm số xác định $Leftrightarrow {{x}^{2}}+4mx+4{{m}^{2}}+3ge 0Leftrightarrow {{left( x+2m right)}^{2}}+3ge 0$ (Luôn đúng).
Ta có ${f}’left( x right)={{left( sqrt{{{x}^{2}}+4mx+4{{m}^{2}}+3} right)}^{prime }}=frac{x+2m}{sqrt{{{x}^{2}}+4mx+4{{m}^{2}}+3}}$.
Hàm số nghịch biến trên khoảng $left( -infty ;2 right)$, khi đó
${y}’le 0text{ }left( forall xin left( -infty ;2 right) right)Leftrightarrow frac{x+2m}{sqrt{{{x}^{2}}+4mx+4{{m}^{2}}+3}}le 0text{ }left( forall xin left( -infty ;2 right) right)$
Suy ra $x+2mle 0text{ }left( forall xin left( -infty ;2 right) right)Leftrightarrow mle -frac{x}{2}text{ }left( forall xin left( -infty ;2 right) right)Leftrightarrow mle frac{-2}{2}=-1$. Chọn A.
| Ví dụ 19: Tìm tất cả các giá trị của tham số m để hàm số $y={{x}^{3}}-3m{{x}^{2}}+3left( 2m-1 right)x+1$ nghịch biến trên đoạn có độ dài bằng 2?
A. $m=0,text{ }m=2$. B. $m=1$. C. $m=0$. D. $m=2$. |
Lời giải
Ta có ${y}’={{left[ {{x}^{3}}-3m{{x}^{2}}+3left( 2m-1 right)x+1 right]}^{prime }}=3{{x}^{2}}-6mx+3left( 2m-1 right)$.
Hàm số nghịch biến trên đoạn có độ dài bằng 2 PT ${y}’=0$ là hai nghiệm ${{x}_{1}},text{ }{{x}_{2}}$ thỏa mãn $left| {{x}_{1}}-{{x}_{2}} right|=2$.
Hàm số có hai cực trị, khi đó $text{Δ’}left( {{y}’} right)>0Leftrightarrow 9{{m}^{2}}-9left( 2m-1 right)>0Leftrightarrow {{left( m-1 right)}^{2}}>0Leftrightarrow mne 1$.
Khi đó $left{ begin{array} {} {{x}_{1}}text{+ }{{x}_{2}}=2m \ {} {{x}_{1}}.{{x}_{2}}=2m-1 \ end{array} right.Rightarrow left| {{x}_{1}}-{{x}_{2}} right|=2Leftrightarrow {{left( {{x}_{1}}-{{x}_{2}} right)}^{2}}=4$
$Leftrightarrow {{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-4{{x}_{1}}.{{x}_{2}}=4Leftrightarrow 4{{m}^{2}}-4left( 2m-1 right)=4Leftrightarrow 4{{m}^{2}}-8m=0Leftrightarrow left[ begin{array} {} m=0 \ {} m=2 \ end{array} right.$. Chọn A.
| Ví dụ 20: Tổng các giá trị của tham số m thỏa mãn điều kiện để hàm số $y=frac{1}{3}{{x}^{3}}-m{{x}^{2}}+left( 3-2m right)x+m$ nghịch biến trên đoạn có độ dài bằng $2sqrt{5}$ là:
A. $T=2$. B. $T=-2$. C. $T=-4$. D. $T=4$. |
Lời giải
Ta có: ${y}’={{x}^{2}}-2mx+3-2m$.
Hàm số nghịch biến trên đoạn có độ dài bằng $2sqrt{5}$ khi phương trình ${{x}^{2}}-2mx+3-2m=0left( * right)$ có 2 nghiệm phân biệt thỏa mãn $left| {{x}_{1}}-{{x}_{2}} right|=2sqrt{5}$
Phương trình (*) có 2 nghiệm phân biệt khi $text{Δ’}={{m}^{2}}+2m-3>0$
Theo định lí Vi-et ta có: $left{ begin{array} {} {{x}_{1}}+{{x}_{2}}=2m \ {} {{x}_{1}}.{{x}_{2}}=3-2m \ end{array} right.$
Ta có: $left| {{x}_{1}}-{{x}_{2}} right|=2sqrt{5}Leftrightarrow {{left( {{x}_{1}}-{{x}_{2}} right)}^{2}}=20Leftrightarrow {{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-4{{x}_{1}}{{x}_{2}}=20Leftrightarrow 4{{m}^{2}}+8m-12=20left( t/m right)$
$Leftrightarrow left[ begin{array} {} m=-4 \ {} m=2 \ end{array} right.Rightarrow T=-2$. Chọn B.
| Ví dụ 21: Xác định giá trị của b để hàm số $fleft( x right)=sin x-bx+c$ nghịch biến trên toàn trục số.
A. $ble 1$. B. $b<1$. C. $b>1$. D. $bge 1$. |
Lời giải
Ta có: ${y}’=cos x-b$. Hàm số nghịch biến trên $mathbb{R}$ $Leftrightarrow cos x-ble 0text{ }forall xin mathbb{R}Leftrightarrow bge cos xtext{ }forall xin mathbb{R}Leftrightarrow bge 1$.
Chọn D.
| Ví dụ 22: : Xác định giá trị của m để hàm số $fleft( x right)=sin 2x+mx+c$ đồng biến trên $mathbb{R}$.
A. $mge 2$. B. $-2le mle 2$. C. $m>2$. D. $mge -2$. |
Lời giải
Ta có: ${y}’=2cos 2x+m$.
Hàm số đồng biến trên $mathbb{R}$ $Leftrightarrow {y}’ge 0left( forall xin mathbb{R} right)Leftrightarrow underset{mathbb{R}}{mathop{min }},{y}’=-2+mge 0Leftrightarrow mge 2$. Chọn A.
| Ví dụ 23: Xác định giá trị của m để hàm số $y=msin x+cos x+left( m+1 right)x$ đồng biến trên $mathbb{R}$.
A. $mge 0$. B. $-1le mle 1$. C. $m>1$. D. $mge -1$. |
Lời giải
Ta có: ${y}’=mcos x-sin x+m+1$.Hàm số đồng biến trên $mathbb{R}$ $Leftrightarrow {y}’ge 0left( forall xin mathbb{R} right)$.
$Leftrightarrow underset{mathbb{R}}{mathop{min }},{y}’=-sqrt{{{m}^{2}}+1}+m+1ge 0Leftrightarrow m+1ge sqrt{{{m}^{2}}+1}Leftrightarrow left{ begin{array} {} mge -1 \ {} {{m}^{2}}+2m+1ge {{m}^{2}}+1 \ end{array} right.$
![]() . Chọn A.
. Chọn A.
| Ví dụ 24: Xác định giá trị của tham số m để hàm số $y=left( m-3 right)x-left( 2m+1 right)cos x$ luôn nghịch biến trên $mathbb{R}$.
A. $-4le mle frac{2}{3}$. B. $-4le mle 3$. C. $-1le mle frac{2}{3}$. D. $-1le mle 3$. |
Lời giải
Ta có: ${y}’=m-3+left( 2m+1 right)sin x$. Hàm số nghịch biến trên $mathbb{R}$ $Leftrightarrow {y}’le 0left( forall xin mathbb{R} right)$
$Leftrightarrow underset{mathbb{R}}{mathop{max }},{y}’=m-3+left| 2m+1 right|le 0Leftrightarrow 3-mge left| 2m+1 right|Leftrightarrow left{ begin{array} {} mle 3 \ {} {{left( 3-m right)}^{2}}ge {{left( 2m+1 right)}^{2}} \ end{array} right.Leftrightarrow left{ begin{array} {} mle 3 \ {} 3{{m}^{2}}+10m-8le 0 \ end{array} right.$
$Leftrightarrow -4le mle frac{2}{3}$. Chọn A.
| Ví dụ 25: Tìm tất cả các giá trị của tham số m để hàm số $y={{x}^{3}}-left( 3m+6 right){{x}^{2}}+left( 3{{m}^{2}}+12m right)x+{{m}^{2}}-m$ nghịch biến trên đoạn $left[ 1;3 right]$.
A. $0le mle 1$. B. $left[ begin{array} {} mge 1 \ {} mle 0 \ end{array} right.$. C. $-1le mle 1$. D. $left[ begin{array} {} mge 1 \ {} mle -1 \ end{array} right.$.. |
Lời giải
Ta có: ${y}’=3{{x}^{2}}-6left( m+2 right)x+3left( {{m}^{2}}+4m right)=3left( x-m right)left( x-m-4 right);text{ }{y}’=0Leftrightarrow left[ begin{array} {} x=m \ {} x=m+4 \ end{array} right.$.
Do đó phương trình ${y}’=0$ luôn có 2 nghiệm phân biệt
Bảng biến thiên
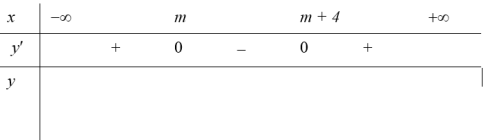
Để hàm số nghịch biến trên $left[ 1;3 right]$ thì $left{ begin{array} {} mle 1 \ {} m+4ge 3 \ end{array} right.Leftrightarrow left{ begin{array} {} mle 1 \ {} mge -1 \ end{array} right.Leftrightarrow -1le mle 1$. Chọn C.
| Ví dụ 26: Tìm tất cả các giá trị của tham số m để hàm số $y={{x}^{3}}-6m{{x}^{2}}+left( 12{{m}^{2}}-3 right)x+m+3$ nghịch biến trên đoạn $left[ 0;1 right]$.
A. $-1le mle 1$. B. $left[ begin{array} {} mge 1 \ {} mle -1 \ end{array} right.$. C. $left[ begin{array} {} mge frac{1}{2} \ {} mle 0 \ end{array} right.$. D. $0le mle frac{1}{2}$. |
Lời giải
Ta có: ${y}’=3{{x}^{2}}-12mx+12{{m}^{2}}-3=3left( x-2m+1 right)left( x-2m-1 right);text{ }{y}’=0Leftrightarrow left[ begin{array} {} x=2m+1 \ {} x=2m-1 \ end{array} right.$.
Do đó phương trình![]() luôn có 2 nghiệm phân biệt
luôn có 2 nghiệm phân biệt
Bảng biến thiên
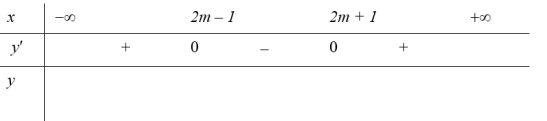
Để hàm số nghịch biến trên $left[ 0;1 right]$ thì $left{ begin{array} {} 2m-1le 0 \ {} 2m+1ge 1 \ end{array} right.Leftrightarrow left{ begin{array} {} mle frac{1}{2} \ {} mge 0 \ end{array} right.Leftrightarrow 0le mle frac{1}{2}$. Chọn D.
| Ví dụ 27: Số giá trị nguyên của tham số m thuộc đoạn $left[ -20;20 right]$ để hàm số $y={{x}^{3}}-3left( m-1 right){{x}^{2}}-left( 9{{m}^{2}}-6m right)x+2m+1$ nghịch biến trên khoảng $left( 2;4 right)$ là:
A. 17. B. 36. C. 19. D. 41. |
Lời giải
Ta có: ${y}’=3{{x}^{2}}-6left( m-1 right)x-3mleft( 3m-2 right)=3left( x+m right)left[ x-left( 3m-2 right) right]<0$
Để hàm số nghịch biến trên khoảng $left( 2;4 right)$ thì:
TH1: $-mle 2<4le 3m-2Leftrightarrow left{ begin{array} {} mge -2 \ {} mge 2 \ end{array} right.Leftrightarrow mge 2$.
TH2: $3m-2le 2<4le -mLeftrightarrow left{ begin{array} {} mle -4 \ {} mle frac{4}{3} \ end{array} right.Leftrightarrow mle -4$.
Kết hợp $left{ begin{array} {} min mathbb{Z} \ {} min left[ -20;20 right] \ end{array} right.Rightarrow $có 36 giá trị nguyên của m. Chọn B.
| Ví dụ 28: Cho hàm số $y=2{{x}^{3}}-3left( m+1 right){{x}^{2}}+6mx$. Số giá trị nguyên dương của m để hàm số đã cho đồng biến trên khoảng $left( 2;+infty right)$ là:
A. 1. B. 2. C. 3. D. 4. |
Lời giải
Yêu cầu bài toán $Leftrightarrow {y}’=6left( {{x}^{2}}-mleft( x+1 right)x+m right)ge 0text{ }left( forall xin left( 2;+infty right) right)$
$Leftrightarrow left( x-1 right)left( x-m right)ge 0text{ }left( forall xin left( 2;+infty right) right)Leftrightarrow xge mtext{ }left( forall xin left( 2;+infty right) right)Leftrightarrow 2ge m$.
Kết hợp $min {{mathbb{Z}}^{+}}Rightarrow m=left{ 1;2 right}$. Chọn B.
| Ví dụ 29: Cho hàm số $y=2{{x}^{3}}-3left( m+2 right){{x}^{2}}+12mx+1$. Gọi S là tập hợp các giá trị nguyên của $min left[ -10;10 right]$ để hàm số đã cho đồng biến trên khoảng $left( 3;+infty right)$. Số phần tử của tập hợp S là
A. 13. B. 14. C. 15. D. 16. |
Lời giải
Ta có: ${y}’=6{{x}^{2}}-6left( m+2 right)x+12mge 0text{ }Leftrightarrow {{x}^{2}}-left( m+2 right)x+2mge 0$.
Giả thiết $Leftrightarrow left( x-m right)left( x-2 right)ge 0text{ }left( forall x>3 right)Leftrightarrow x-mge 0text{ }left( forall x>3 right)Leftrightarrow xge mtext{ }left( forall x>3 right)Leftrightarrow 3ge m$.
Kết hợp $left{ begin{array} {} min mathbb{Z} \ {} min left[ -10;10 right] \ end{array} right.Rightarrow $có 14 giá trị của m. Chọn B.
| Ví dụ 30: Cho hàm số $y={{x}^{3}}-3m{{x}^{2}}+3left( {{m}^{2}}-1 right)x+1$. Gọi S là tập hợp các giá trị nguyên của $min left[ -20;20 right]$ để hàm số đã cho đồng biến trên khoảng $left( 0;+infty right)$. Số phần tử của tập hợp S là
A. 22. B. 19. C. 21. D. 20. |
Lời giải
Ta có: ${y}’=3{{x}^{2}}-6mx+3left( {{m}^{2}}-1 right)$. Ta có: ${y}’ge 0Leftrightarrow {{x}^{2}}-2mx+left( {{m}^{2}}-1 right)ge 0$
$Leftrightarrow left( x-m-1 right)left( x-m+1 right)ge 0Leftrightarrow left{ begin{array} {} xge m+1 \ {} xle m-1 \ end{array} right.$.
Do vậy hàm số đồng biến trên $left( -infty ;m-1 right]$ và $left[ m+1;+infty right)$
Để hàm số đã cho đồng biến trên x$left( 0;+infty right)Leftrightarrow m+1le 0Leftrightarrow mle -1$
.Kết hợp $left{ begin{array} {} min mathbb{Z} \ {} min left[ -20;20 right] \ end{array} right.Rightarrow $có 20 giá trị nguyên của m. Chọn D.
| Ví dụ 31: Cho hàm số $y=-{{x}^{4}}+4left( 3m-2 right){{x}^{2}}+2m+1$. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $left[ -20;20 right]$ để hàm số đồng biến trên khoảng $left( -infty ;-2 right)$
A. 22. B. 23. C. 21. D. 20. |
Lời giải
Ta có: ${y}’=-4{{x}^{3}}+8left( 3m-2 right)x$. Hàm số đồng biến trên khoảng $left( -infty ;-2 right)$.
$Leftrightarrow -4{{x}^{3}}+8left( 3m-2 right)xge 0text{ }left( forall xin left( -infty ;-2 right) right)Leftrightarrow {{x}^{2}}-2left( 3m-2 right)ge 0text{ }left( forall xin left( -infty ;-2 right) right)$
(Do $-4xge 0text{ }left( forall xin left( -infty ;-2 right) right)$)
$Leftrightarrow 2left( 3m-2 right)le {{x}^{2}}text{ }left( forall xin left( -infty ;-2 right) right)Leftrightarrow 2left( 3m-2 right)le underset{left( -infty ;-2 right)}{mathop{min }},{{x}^{2}}=4Leftrightarrow 3m-2le 2Leftrightarrow mle frac{4}{3}$.
Kết hợp $left{ begin{array} {} min mathbb{Z} \ {} min left[ -20;20 right] \ end{array} right.Rightarrow $có 22 giá trị của m. Chọn A.
| Ví dụ 32: Cho hàm số $y={{x}^{4}}-2left( 2m+3 right){{x}^{2}}+m-1$. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $left[ -10;10 right]$ để hàm số nghịch biến trên khoảng $left( 0;3 right)$.
A. 8. B. 7. C. 6. D. 5. |
Lời giải
Ta có: ${y}’=4{{x}^{3}}-4left( 2m+3 right)x$. Hàm số nghịch biến trên khoảng $left( 0;3 right)$.
$Leftrightarrow 4{{x}^{3}}-4left( 2m+3 right)xle 0text{ }left( forall xin left( 0;3 right) right)Leftrightarrow {{x}^{2}}-left( 2m+3 right)le 0text{ }left( forall xin left( 0;3 right) right)$
$Leftrightarrow {{x}^{2}}le 2m+3text{ }left( forall xin left( 0;3 right) right)Leftrightarrow 2m+3ge 9Leftrightarrow mge 3$
Kết hợp $left{ begin{array} {} min mathbb{Z} \ {} min left[ -10;10 right] \ end{array} right.Rightarrow $có 8 giá trị của m. Chọn A.
| Ví dụ 33: Cho hàm số $y={{x}^{4}}-8left( {{m}^{2}}-5 right){{x}^{2}}+3m-1$. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $left[ -10;10 right]$ để hàm số đồng biến trên khoảng $left( 3;+infty right)$.
A. 4. B. 5. C. 6. D. 7.. |
Lời giải
Ta có: ${y}’=4{{x}^{3}}-8left( {{m}^{2}}-5 right)x$. Hàm số đồng biến trên khoảng $left( 3;+infty right)$.
$Leftrightarrow 4{{x}^{3}}-8left( {{m}^{2}}-5 right)xge 0text{ }left( forall xin left( 3;+infty right) right)Leftrightarrow {{x}^{2}}-2left( {{m}^{2}}-5 right)ge 0text{ }left( forall xin left( 3;+infty right) right)$.
$Leftrightarrow 2left( {{m}^{2}}-5 right)le {{x}^{2}}text{ }left( forall xin left( 3;+infty right) right)Leftrightarrow 2left( {{m}^{2}}-5 right)le 9Leftrightarrow {{m}^{2}}le frac{19}{2}$.
Kết hợp $min mathbb{Z}Rightarrow m=left{ 0;pm 1;pm 2;pm 3 right}$. Chọn D.