LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Cùng pha
■ Xét hai dao động cùng pha x và y, có phương trình:
$left{ begin{matrix}x=Acos left( omega t+varphi right) \x=Bcos left( omega t+varphi right) \end{matrix} right.Rightarrow left{ begin{matrix}frac{x}{A}=cos left( omega t+varphi right) \frac{y}{B}=cos left( omega t+varphi right) \end{matrix} right.Rightarrow Rightarrow x=frac{A}{B}yRightarrow left( C>0 right).$
+) Tại mọi thời điểm x và y luôn cùng dấu.
+) Đồ thị x phụ thuộc vào y là một đoạn thẳng đi qua gốc tọa độ có hệ số góc dương (C).
VD: +) ${{F}_{hp}}=ma:{{F}_{hp}}$và a là 2 dao động điều hòa cùng pha với nhau
+) $p=mv:p$và v là 2 dao động điều hòa cùng pha với nhau…
2. Ngược pha
■ Xét hai dao động ngược pha x và y, có phương trình:
$left{ begin{matrix}x=Acos left( omega t+varphi right) \y=Bcos left( omega t+varphi +pi right) \end{matrix} right.begin{matrix}{} \=-Bcos left( omega t+varphi right) \end{matrix}Rightarrow left{ begin{matrix}frac{x}{A}=cos left( omega t+varphi right) \-frac{y}{B}=cos left( omega t+varphi right) \end{matrix}Rightarrow {{}_{{}}} right.$
$Leftrightarrow x=-frac{A}{B}yLeftrightarrow left( C>0 right)$
+) Tại mọi thời điểm x, y luôn trái dấu.
+) Đồ thị x phụ thuộc vào y là một đoạn thẳng có hệ số góc âm (-C).
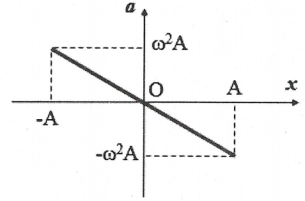
VD: +) $a=-{{omega }^{2}}x:a$và x là 2 dao động điều hòa ngược pha với nhau.
+) ${{F}_{hp}}=-kx:{{F}_{hp}},x$là 2 dao động điều hòa ngược pha nhau…
3. Vuông pha
■ Xét hai dao động vuông pha x và y, có phương trình:
$left{ begin{matrix}x=Acos left( omega t+varphi right) \y=Bcos left( omega t+varphi +pi /2 right) \end{matrix} right.begin{matrix}{} \=-Bsin left( omega t+varphi right) \end{matrix}Rightarrow left{ begin{matrix}frac{x}{A}=cos left( omega t+varphi right) \frac{y}{B}=-sin left( omega t+varphi right) \end{matrix}Rightarrow {{left( frac{x}{A} right)}^{2}}+{{left( frac{y}{B} right)}^{2}}=1 right.$
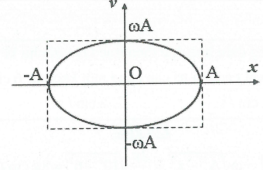
+) Đồ thị x phụ thuộc vào y là một Elip.
VD: +) $left( x,v right)$vuông pha: ${{left( frac{x}{A} right)}^{2}}+{{left( frac{v}{Aomega } right)}^{2}}=1Rightarrow left{ begin{matrix}{{A}^{2}}={{x}^{2}}+frac{{{v}^{2}}}{{{omega }^{2}}} \v=pm omega sqrt{{{A}^{2}}-{{x}^{2}}} \end{matrix} right.$
+) $left( v,a right)$ vuông pha: ${{left( frac{v}{{{v}_{max }}} right)}^{2}}+{{left( frac{a}{{{a}_{max }}} right)}^{2}}=1$
Chú ý: Sử dụng mối quan hệ độc lập thời gian của hai đại lượng dao động điều hòa vuông pha:
+) Nếu $frac{x}{A}=0Rightarrow {{left( frac{y}{B} right)}^{2}}=1Rightarrow y=pm B:$ tức, một đại lượng đang ở vtcb thì đại lượng kia đang ở biên
+) Nếu $frac{x}{A}=pm frac{1}{2}Rightarrow frac{y}{B}=pm frac{sqrt{3}}{2}.$
+) Nếu $frac{x}{A}=pm frac{1}{sqrt{2}}Rightarrow frac{y}{B}=pm frac{1}{sqrt{2}.}$
4. Bài tập minh họa
| Tính tần số góc của một vật dao động điều hoà. Biết
a) tại thời điểm ${{t}_{1}}$, vật có li độ ${{x}_{1}}$ và vận tốc là ${{v}_{1}}$, tại thời điểm ${{t}_{2}}$ vật có li độ là ${{x}_{2}}left( {{x}_{1}}ne {{x}_{2}} right)$ và vận tốc là ${{v}_{2}}$. b) tại thời điểm ${{t}_{1}}$ vật có vận tốc là ${{x}_{1}}$và gia tốc là a1, tại thời điểm ${{t}_{2}}$vật có vận tốc là ${{v}_{2}}$và gia tốc là ${{a}_{2}}$. |
Lời giải chi tiết:
a) Do $overrightarrow{x}bot overrightarrow{v}$ suy ra ${{left( frac{x}{A} right)}^{2}}+{{left( frac{v}{-omega A} right)}^{2}}=1.$
Theo đề bài ta có $left{ begin{matrix}{{left( frac{{{x}_{1}}}{A} right)}^{2}}+{{left( frac{{{v}_{1}}}{omega A} right)}^{2}}=1 \{{left( frac{{{x}_{2}}}{A} right)}^{2}}+{{left( frac{{{v}_{2}}}{omega A} right)}^{2}}=1 \end{matrix} right.Leftrightarrow x_{1}^{2}+frac{v_{1}^{2}}{{{omega }^{2}}}=x_{2}^{2}+frac{v_{2}^{2}}{{{omega }^{2}}}={{A}^{2}}Rightarrow {{omega }^{2}}=frac{v_{1}^{2}-v_{2}^{2}}{x_{2}^{2}-x_{1}^{2}}$
$.$ Đặc biệt khi $left{ begin{matrix}{{v}_{2}}=0Rightarrow left| {{x}_{2}} right|=A \{{v}_{1}}={{v}_{max }}Rightarrow {{x}_{1}}=0 \end{matrix} right.Rightarrow omega =frac{{{v}_{max }}}{A}.$
b) Do $overrightarrow{v}bot overrightarrow{a}Rightarrow left{ begin{matrix}frac{v_{1}^{2}}{{{omega }^{2}}}+frac{a_{1}^{2}}{{{omega }^{4}}}={{A}^{2}} \frac{v_{2}^{2}}{{{omega }^{2}}}+frac{a_{2}^{2}}{{{omega }^{4}}}={{A}^{2}} \end{matrix}Rightarrow {{omega }^{2}} right.=frac{a_{2}^{2}-a_{1}^{2}}{v_{1}^{2}-v_{2}^{2}}Rightarrow omega =sqrt{frac{a_{2}^{2}-a_{1}^{2}}{v_{1}^{2}-v_{2}^{2}}.}$
$.$ Đặc biệt khi $left{ begin{matrix}{{v}_{2}}=0Rightarrow left| {{a}_{2}} right|={{a}_{max }} \{{v}_{1}}={{v}_{max }}Rightarrow {{a}_{1}}=0 \end{matrix} right.Rightarrow omega =frac{{{a}_{max }}}{{{v}_{max }}}.$
