CỰC TRỊ CỦA HÀM TRỊ TUYỆT ĐỐI – CÁCH GIẢI BÀI TẬP CÓ ĐÁP ÁN
@ Phương pháp giải: Loại 1: Cực trị hàm số $y=left| fleft( x right) right|.$
Ta có: $y=left| fleft( x right) right|Rightarrow y’=frac{f’left( x right).fleft( x right)}{left| fleft( x right) right|}$ do đó
Số điểm cực trị của hàm số $y=left| fleft( x right) right|$ là số nghiệm bội lẻ của phương trình $f’left( x right).fleft( x right)=0.$
Như vậy: Nếu gọi m là số điểm cực trị của hàm số $y=fleft( x right)$và n là số giao điểm của đồ thị hàm số $y=fleft( x right)$và trục hoành thì $m+n$ là số điểm cực trị của hàm số $y=left| fleft( x right) right|$ (chú ý ta cần bỏ đi các nghiệm bội chẵn).
Bài tập cực đại cực tiểu hàm trị tuyệt đối loại 1 – có đáp án
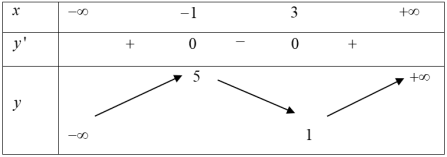
| Bài tập 1: [Đề thi THPT QG năm 2017] Cho hàm số $y=fleft( x right)$ có bảng biến thiên như sau.
Đồ thị của hàm số $y=left| fleft( x right) right|$ có bao nhiêu điểm cực trị? A. 5. B. 3. C. 4. D. 2. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy:
Đồ thị hàm số $y=fleft( x right)$ cắt trục hoành $y=0$ tại 1 điểm nên $m=1.$
Hàm số $y=fleft( x right)$ có 2 điểm cực trị nên $n=2Rightarrow $ Hàm số $y=left| fleft( x right) right|$ có 3 điểm cực trị. Chọn B.
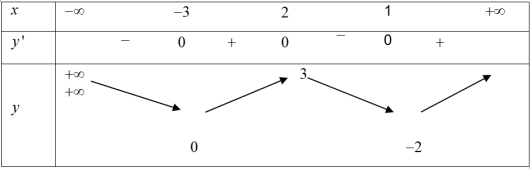
| Bài tập 2: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới:
Số điểm cực trị của hàm số $y=left| fleft( x right) right|$là: A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy:
Hàm số $y=fleft( x right)$có 3 điểm cực trị suy ra $m=3.$
Phương trình $fleft( x right)=0$ có 3 nghiệm (tuy nhiên $x=-1$ là nghiệm kép) suy ra $n=2.$
Do đó hàm số $y=left| fleft( x right) right|$ có $m+n=5$ điểm cực trị. Chọn C.
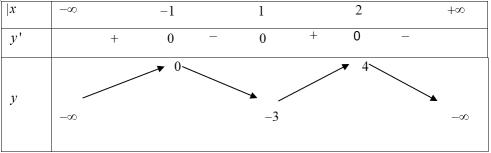
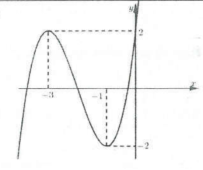
| Bài tập 3: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới đây.
Số điểm cực trị của hàm số $y=left| fleft( x right) right|$là: A. 3. B. 4. C. 5. D. 6. |
Lời giải chi tiết
Dựa vào bảng biến thiên ta thấy:
Hàm số $y=fleft( x right)$có 3 điểm cực trị suy ra $m=3.$
Đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 3 điểm phân biệt (tuy nhiên $x=-1$ là nghiệm kép) nên $n=2.$
Do đó hàm số $y=left| fleft( x right) right|$ có 5 điểm cực trị. Chọn C.
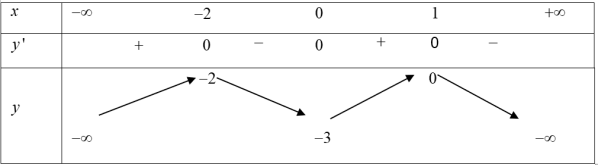
| Bài tập 4: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới đây.
Số điểm cực trị của hàm số $y=left| fleft( x right)+2 right|$là: A. 4. B. 6. C. 3. D. 5. |
Lời giải chi tiết
Đặt $gleft( x right)=fleft( x right)+2Rightarrow g’left( x right)=f’left( x right)$
Phương trình $g’left( x right)=f’left( x right)=0$ có 3 nghiệm phân biệt nên $m=3.$
Phương trình $gleft( x right)=0Leftrightarrow fleft( x right)=-2$ có 3 nghiệm trong đó có 1 nghiệm kép $n=2.$
Do đó hàm số $y=left| fleft( x right)+2 right|$có 5 điểm cực trị. Chọn D.
| Bài tập 5: Số điểm cực trị của hàm số $y=left| {{left( x-1 right)}^{3}}left( x-3 right)left( x+2 right) right|$ là:
A. 4. B. 5. C. 6. D. 7. |
Lời giải chi tiết
Ta có: $y=fleft( x right)$ thì $y’=frac{f’left( x right)fleft( x right)}{left| fleft( x right) right|}$
Xét $fleft( x right)={{left( x-1 right)}^{3}}left( x-3 right)left( x+2 right)$
Ta có: $fleft( x right)=0$ có 3 nghiệm bội lẻ $x=1,x=3,x=-2.$
Lại có: $fleft( x right)={{left( x-1 right)}^{3}}left( {{x}^{2}}-x-6 right)Rightarrow f’left( x right)=3{{left( x-1 right)}^{2}}left( {{x}^{2}}-x-6 right)+{{left( x-1 right)}^{3}}left( 2x-1 right)$
$={{left( x-1 right)}^{2}}left[ 3{{x}^{2}}-3x-18+left( x-1 right)left( 2x-1 right) right]={{left( x-1 right)}^{2}}left( 5{{x}^{2}}-6x-17 right)=0Rightarrow f’left( x right)=0$ có 2 nghiệm bội lẻ. Do đó hàm số đã cho có 5 điểm cực trị. Chọn B.
| Bài tập 6: Số điểm cực trị của hàm số $y=left| {{x}^{4}}+2{{x}^{3}}-{{x}^{2}}-2x right|$ là:
A. 4. B. 5. C. 6. D. 7. |
Lời giải chi tiết
$fleft( x right)=0Leftrightarrow {{x}^{4}}+2{{x}^{3}}-{{x}^{2}}-2x=0Leftrightarrow {{x}^{3}}left( x+2 right)-xleft( x+2 right)=0Leftrightarrow xleft( {{x}^{2}}-1 right)left( x+2 right)=0$có 4 nghiệm bội lẻ.
Phương trình $f’left( x right)=4{{x}^{3}}+4{{x}^{2}}-2x-2=0Leftrightarrow 2left( 2{{x}^{2}}-1 right)left( x+1 right)=0$ có 3 nghiệm bội lẻ.
Do đó hàm số đã cho có $4+3=7$ điểm cực trị. Chọn D.
| Bài tập 7: Số giá trị nguyên của tham số m để hàm số$y=left| {{x}^{4}}-4{{x}^{3}}+4{{x}^{2}}+m right|$ có 7 điểm cực trị là:
A. 0. B. 9. C. 8. D. vô số. |
Lời giải chi tiết
Xét $fleft( x right)={{x}^{4}}-4{{x}^{3}}+4{{x}^{2}}+m$
Phương trình $f’left( x right)=4{{x}^{3}}-12{{x}^{2}}+8x=0Leftrightarrow left[ begin{matrix} x=0 \ x=1 \ x=2 \end{matrix} right.$ có 3 nghiệm bội lẻ.
Để hàm số $y=left| {{x}^{4}}-4{{x}^{3}}+4{{x}^{2}}+m right|$ có 7 điểm cực trị thì phương trình
$fleft( x right)=0Leftrightarrow {{x}^{4}}-4{{x}^{3}}+4{{x}^{2}}=-m(*)$ phải có 4 nghiệm phân biệt.
Lập BBT cho hàm số $gleft( x right)={{x}^{4}}-4{{x}^{3}}+4x$ ta được:
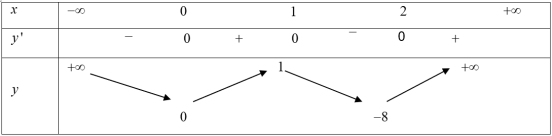
Phương trình (*) có 4 nghiệm phân biệt khi $0<-m<1.$
Vậy không có giá trị nguyên của m nào thỏa mãn yêu cầu bài toán. Chọn A.
| Bài tập 8: Số giá trị nguyên của tham số m để hàm số$y=left| {{x}^{4}}-4{{x}^{3}}-8{{x}^{2}}+m right|$ có 7 điểm cực trị là:
A. 129. B. 2. C. 127. D. 3. |
Lời giải chi tiết
Phương trình $f’left( x right)=4{{x}^{3}}-12{{x}^{2}}-16x=0Leftrightarrow left[ begin{matrix} x=0text{ } \ x=-1 \ x=4text{ } \end{matrix} right.$ có 3 nghiệm bội lẻ.
Để hàm số $y=left| {{x}^{4}}-4{{x}^{3}}-8{{x}^{2}}+m right|$ có 7 điểm cực trị thì phương trình
$fleft( x right)=0Leftrightarrow {{x}^{4}}-4{{x}^{3}}-8{{x}^{2}}=-m(*)$ có 4 nghiệm phân biệt. Lập BBT cho hàm số $gleft( x right)={{x}^{4}}-4{{x}^{3}}-8{{x}^{2}}$ ta được:
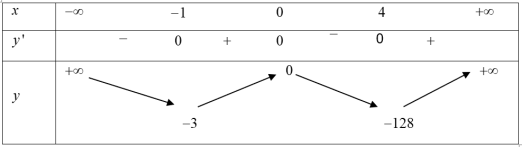
Phương trình (*) có 4 nghiệm phân biệt khi $-3<-m<0.$
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Chọn B.
| Bài tập 9: [Đề thi tham khảo Bộ GD{}ĐT năm 2018] Có bao nhiêu giá trị nguyên của tham số m để hàm số$y=left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m right|$ có 7 điểm cực trị?
A. 3. B. 5. C. 6. D. 4. |
Lời giải chi tiết
Đặt $fleft( x right)=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+mxrightarrow{{}}f’left( x right)=12{{x}^{3}}-12{{x}^{2}}-24x;forall xin mathbb{R}.$
Phương trình $f’left( x right)=0$ có 3 nghiệm phân biệt.
Để hàm số đã cho có 7 điểm cực trị $Leftrightarrow fleft( x right)=0Leftrightarrow gleft( x right)=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}=m$ có 4 nghiệm phân biệt.
Mà $f’left( x right)=0$ có 3 nghiệm phân biệt $Rightarrow fleft( x right)=-m$ có 4 nghiệm phân biệt.
Dựa vào BBT hàm số $fleft( x right)$, để (*) có 4 nghiệm phân biệt$Leftrightarrow -5<-m<0Leftrightarrow min left( 0;5 right)$.
Kết hợp với $min mathbb{Z}$ suy ra có tất cả 4 giá trị nguyên cần tìm. Chọn D.
| Bài tập 10: Cho hàm số $fleft( x right)=left| 2{{x}^{3}}-3{{x}^{2}}-12x+m+2 right|$. Số giá trị nguyên âm của tham số m để hàm số đã cho có 5 điểm cực trị là:
A. 26. B. 25. C. 8. D. 9. |
Lời giải chi tiết
Dễ thấy hàm số $gleft( x right)=2{{x}^{3}}-3{{x}^{2}}-12x+m+2$ có $y’=6{{x}^{2}}-6x-12=0Leftrightarrow left[ begin{matrix} x=-1 \ x=2text{ } \end{matrix} right.$
Suy ra hàm số ![]() có 2 điểm cực trị.
có 2 điểm cực trị.
Để hàm số $fleft( x right)=left| 2{{x}^{3}}-3{{x}^{2}}-12x+m+2 right|$ có 5 điểm cực trị thì phương trình
$2{{x}^{3}}-3{{x}^{2}}-12x+m+2Leftrightarrow hleft( x right)=2{{x}^{3}}-3{{x}^{2}}-12x+2=-m$ có 3 nghiệm phân biệt
Dễ thấy $left{ begin{matrix} hleft( -1 right)=9text{ } \ hleft( 2 right)=-18 \end{matrix} right.Rightarrow hleft( x right)=-m$ có 3 nghiệm phân biệt khi $-18<-mm>-9$
Vậy có 8 giá trị nguyên cần tìm. Chọn C.
| Bài tập 11: Có bao nhiêu giá trị nguyên của tham số m để hàm số $fleft( x right)=left| 2{{x}^{4}}-4left( m+8 right){{x}^{2}}+m-1 right|$ có 5 điểm cực trị?
A. 9. B. 10. C. 8. D. vô số. |
Lời giải chi tiết
Xét hàm số $fleft( x right)=left| 2{{x}^{4}}-4left( m+8 right){{x}^{2}}+m-1 right|$
TH1: Hàm số $y=fleft( x right)$ có một điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại nhiều nhất 2 điểm nên hàm số $y=left| fleft( x right) right|$ không thể có 5 điểm cực trị.
TH2: Hàm số $y=fleft( x right)$ có 3 điểm cực trị khi $ab<0Leftrightarrow 2.left[ -4left( m+8 right) right]-8.$
Để hàm số $y=left| fleft( x right) right|$ có 5 điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 2 điểm phân biệt. Vì hàm số $y=fleft( x right)$ có $a=2>0$ nên có BTT như hình vẽ.

Đồ thị hàm số cắt trục hoành (đường thẳng $y=0$) tại 2 điểm phân biệt khi $0ge m-1Leftrightarrow mle 1.$
(Trong trường dấu bằng xảy ra $m=1Rightarrow $ phương trình có 2 nghiệm đơn và một nghiệm kép $x=0$ nên chỉ có điểm cực trị).
Vậy $-8<mle 1.$ Kết hợp $min mathbb{Z}Rightarrow $ có 9 giá trị nguyên của tham số m. Chọn A.
| Bài tập 12: Có bao nhiêu giá trị nguyên của tham số $min left[ -10;10 right]$ để hàm số$y=left| {{x}^{4}}-2left( m+4 right){{x}^{2}}+9 right|$ có 7 điểm cực trị?
A. 9. B. 11. C. 10. D. 4 |
Lời giải chi tiết
Xét hàm số $fleft( x right)=2{{x}^{4}}-2left( m+4 right){{x}^{2}}+4$
TH1: Hàm số $y=fleft( x right)$ có một điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại nhiều nhất 2 điểm nên hàm số $y=left| fleft( x right) right|$ không thể có 7 điểm cực trị.
TH2: Hàm số $y=fleft( x right)$ có 3 điểm cực trị khi $ab<0Leftrightarrow 1.left[ -2left( m+4 right) right]-4.$
Để hàm số $y=left| fleft( x right) right|$ có 7 điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 4 điểm phân biệt. Ta có: $f’left( x right)=4{{x}^{3}}-4left( m+4 right)x=0Leftrightarrow left[ begin{matrix} x=0text{ } \ {{x}^{2}}=m+4=x_{0}^{2} \end{matrix} right..$
Hàm số có BTT như hình vẽ:
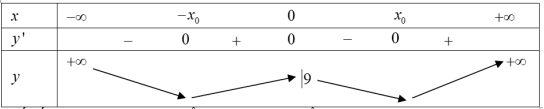
Đồ thị hàm số cắt trục hoành (đường thẳng $y=0$) tại 4 điểm phân biệt khi
$begin{array} {} fleft( pm {{x}_{0}} right)=fleft( sqrt{m+4} right)<0 \ {} Leftrightarrow {{left( m+4 right)}^{2}}-2{{left( m+4 right)}^{2}}+99Leftrightarrow left[ begin{matrix} m>-1 \ m-1.$ Kết hợp $left{ begin{matrix} min mathbb{Z}text{ } \ min left[ -10;10 right] \end{matrix} right.Rightarrow m=left{ 0;1;…10 right}Rightarrow $ có 11 giá trị của m. Chọn B.
| Bài tập 13: Có bao nhiêu giá trị nguyên của tham số $min left[ -20;20 right]$ để hàm số$y=left| {{x}^{4}}-2left( m+1 right){{x}^{2}}+8 right|$ có 7 điểm cực trị?
A. 9. B. 11. C. 12. D. 7. |
Lời giải chi tiết
Xét hàm số $fleft( x right)={{x}^{4}}-2left( m+1 right){{x}^{2}}+8$
TH1: Hàm số $y=fleft( x right)$ có một điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại nhiều nhất 2 điểm nên hàm số $y=left| fleft( x right) right|$ không thể có 7 điểm cực trị.
TH2: Hàm số $y=fleft( x right)$ có 3 điểm cực trị khi $ab<0Leftrightarrow 1.left[ -2left( m+1 right) right]-1.$
Để hàm số $y=left| fleft( x right) right|$ có 7 điểm cực trị thì đồ thị hàm số $y=fleft( x right)$ cắt trục hoành tại 4 điểm phân biệt. Ta có: $f’left( x right)=4{{x}^{3}}-4left( m+1 right)x=0Leftrightarrow left[ begin{matrix} x=0text{ } \ {{x}^{2}}=m+1=x_{0}^{2} \end{matrix} right..$
Hàm số có BTT như hình vẽ:

Đồ thị hàm số cắt trục hoành (đường thẳng $y=0$) tại 4 điểm phân biệt khi
$begin{array} {} fleft( pm {{x}_{0}} right)=fleft( sqrt{m+1} right)<0 \ {} Leftrightarrow {{left( m+1 right)}^{2}}-2{{left( m+1 right)}^{2}}+88Leftrightarrow left[ begin{matrix} m>-1+2sqrt{2} \ m-1-2sqrt{2}.$ Kết hợp $left{ begin{matrix} min mathbb{Z}text{ } \ min left[ -20;20 right] \end{matrix} right.Rightarrow m=left{ 2;3;…10 right}Rightarrow $ có 9 giá trị của m. Chọn A.
Phương pháp giải: Loại 2: Cực trị hàm số $y=fleft( left| x right| right).$
Ta có: $y=fleft( left| x right| right)Rightarrow y’=frac{x}{left| x right|}.f’left( left| x right| right)$ từ đó ta có nhận xét sau:
– Hàm số đạt cực trị tại điểm $x=0.$
– Số điểm cực trị dương của hàm số $y=fleft( x right)$là m thì số điểm cực trị của hàm số $y=fleft( left| x right| right)$ là $2m+1$.
| Bài tập 1: Cho hàm số $fleft( x right)=6{{x}^{5}}-15{{x}^{4}}-10{{x}^{3}}+30{{x}^{2}}+1,$ số điểm cực trị của hàm số $y=fleft( left| x right| right)$ là:
A. 4. B. 5. C. 6. D. 7. |
Lời giải chi tiết
Ta có: $f’left( x right)=30{{x}^{4}}-60{{x}^{3}}-30{{x}^{2}}+60x=0$
$Leftrightarrow xleft( {{x}^{3}}-2{{x}^{2}}-x-2 right)=xleft( x-1 right)left( x+1 right)left( x-2 right)$
Lại có: $y=fleft( left| x right| right)Rightarrow y’=frac{x}{left| x right|}.left| x right|left( left| x right|-1 right)left( left| x right|+1 right)left( left| x right|-2 right)$đổi dấu qua 5 điểm $x=0;x=pm 1;x=pm 2$ nên hàm số $y=fleft( left| x right| right)$có 5 điểm cực trị. Chọn B.
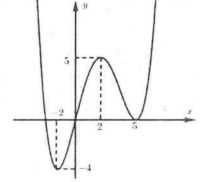
| Bài tập 2: Cho hàm số $y=fleft( x right)$ xác định trên $mathbb{R}$ và có bảng biến thiên như hình vẽ dưới đây.
Số điểm cực trị của hàm số $y=fleft( left| x right| right)$là: A. 2. B. 3. C. 4. D. 5. |
Lời giải chi tiết
Hàm số $y=fleft( x right)$ có 2 điểm cực trị có hoành độ dương là $left( 2;-1 right)$ và $left( 5;0 right)$
Do đó hàm số $y=fleft( left| x right| right)$ có $2.2+1=5$ điểm cực trị. Chọn D.
| Bài tập 3: Cho hàm số $y=fleft( x right)$ có bảng biến thiên như hình vẽ dưới
Số điểm cực trị của hàm số $y=fleft( left| x right|+1 right)$là A. 4. B. 6. C. 5. D. 3. |
Lời giải chi tiết
Ta có: $y’=left( left| x right|+1 right)’.f’left( left| x right|+1 right)=frac{x}{left| x right|}.f’left( left| x right|+1 right)=0Leftrightarrow left[ begin{matrix} x=0text{ } \ f’left( left| x right|+1 right)=0 \end{matrix} right.(*)$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ begin{matrix} x=-1 \ x=0text{ } \ x=2text{ } \end{matrix} right.$
Suy ra $f’left( left| x right|+1 right)=0Leftrightarrow left[ begin{matrix} left| x right|+1=-1 \ left| x right|+1=0text{ } \ left| x right|+1=2text{ } \end{matrix} right.$hệ có 2 nghiệm.
Do đó (*) có 3 nghiệm phân biệt nên hàm số có 3 điểm cực trị. Chọn D.
| Ví dụ 4: Cho hàm số $y=fleft( x right)$ xác định trên $mathbb{R}$ và có đồ thị hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số $m>-20$ để hàm số$y=fleft( left| x right|+m right)$ có 5 điểm cực trị A. 15. B. 19. C. 16. D. 18. |
Lời giải
Ta có: $y’=left( left| x right|+m right)’.f’left( left| x right|+m right)=frac{x}{left| x right|}.f’left( left| x right|+m right)=0Leftrightarrow left[ begin{matrix} x=0text{ } \ f’left( left| x right|+m right)=0 \end{matrix} right.$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ begin{matrix} x=-3 \ x=-1 \end{matrix} right.$
Do đó $f’left( left| x right|+m right)=0Leftrightarrow left[ begin{matrix} left| x right|+m=-3 \ left| x right|+m=-1 \end{matrix} right.Leftrightarrow left[ begin{matrix} left| x right|=-3-m \ left| x right|=-1-m \end{matrix} right.$(*)
Hàm số có 5 điểm cực trị khi (*) có 4 nghiệm phân biệt khác 0 $Leftrightarrow left[ begin{matrix} -3-m>0 \ -1-m>0 \end{matrix} right.Leftrightarrow m-20 \end{matrix} right.Rightarrow $ có 18 giá trị nguyên của m. Chọn D.
| Ví dụ 5: Cho hàm số $y=fleft( x right)$ xác định trên $mathbb{R}$ và có đồ thị hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số $min left[ -10;10 right]$ để hàm số$y=fleft( left| x right|+m right)$ có 7 điểm cực trị A. 8. B. 9. C. 12. D. 13. |
Lời giải
Ta có: $y’=left( left| x right|+m right)’.f’left( left| x right|+m right)=frac{x}{left| x right|}.f’left( left| x right|+m right)=0Leftrightarrow left[ begin{matrix} x=0text{ } \ f’left( left| x right|+m right)=0 \end{matrix} right.$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ begin{matrix} x=-2 \ begin{array} {} x=-2 \ {} x=5text{ } \ end{array} \end{matrix} right.$
Do đó $f’left( left| x right|+m right)=0Leftrightarrow left[ begin{matrix} left| x right|+m=-2 \ begin{array} {} left| x right|+m=2text{ } \ {} left| x right|+m=5 \ end{array} \end{matrix} right.Leftrightarrow left[ begin{matrix} left| x right|=-2-m \ begin{array} {} left| x right|=2-mtext{ } \ {} left| x right|=5-m \ end{array} \end{matrix} right.(*)$
Hàm số có 7 điểm cực trị khi (*) có 6 nghiệm phân biệt khác 0 $Leftrightarrow left[ begin{matrix} -2-m>0 \ begin{array} {} 2-m>0text{ } \ {} 5-m>0 \ end{array} \end{matrix} right.Leftrightarrow m<-2.$
Kết hợp $left{ begin{matrix} min mathbb{Z}text{ } \ min left[ -10;10 right] \end{matrix} right.Rightarrow $ có 8 giá trị nguyên của m. Chọn A.
| Ví dụ 6: Cho hàm số $y={{x}^{3}}-3left( m-1 right){{x}^{2}}+6mx+2.$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $left[ -100;100 right]$ để hàm số$fleft( left| x right| right)$ có 5 điểm cực trị?
A. 100. B. 99. C. 97. D. 96. |
Lời giải
Để hàm số $fleft( left| x right| right)$ có 5 điểm cực trị thì hàm số $y=fleft( x right)$phải có 2 điểm cực trị có hoành độ dương.
Ta có: $f’left( x right)=3{{x}^{2}}-6left( m-1 right)x+6m=0Leftrightarrow {{x}^{2}}-2left( m-1 right)x+2mtext{ }(*)$
Giả thiết bài toán $Leftrightarrow left( * right)$ có 2 nghiệm dương phân biệt $Leftrightarrow left{ begin{matrix} Delta ‘={{left( m-1 right)}^{2}}-2m>0 \ S=2left( m-1 right)>0text{ } \ P=2m>0text{ } \end{matrix} right.Leftrightarrow m>2+sqrt{3}.$
Kết hợp $left{ begin{matrix} min mathbb{Z}text{ } \ min left[ -100;100 right] \end{matrix} right.Rightarrow $ có 97 giá trị nguyên của m. Chọn C.
| Ví dụ 7: Cho hàm số $y=fleft( x right)=2{{x}^{3}}-3left( m+1 right){{x}^{2}}+6left( {{m}^{2}}-9 right)x+4.$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $left[ -100;100 right]$ để hàm số$fleft( left| x right| right)$ có đúng 3 điểm cực trị?
A. 6. B. 7. C. 8. D. 9. |
Lời giải
Để hàm số $fleft( left| x right| right)$ có đúng 3 điểm cực trị thì hàm số $y=fleft( x right)$phải có đúng 1 điểm cực trị có hoành độ dương.
Ta có: $f’left( x right)=6{{x}^{2}}-6left( m+1 right)x+6left( {{m}^{2}}-9 right)=0Leftrightarrow {{x}^{2}}-left( m+1 right)x+{{m}^{2}}-9=0text{ }(*)$
Giả thiết bài toán thỏa mãn khi (*) có 2 nghiệm trái dấu hoặc (*) có 1 nghiệm bằng 0 và 1 nghiệm dương. TH1: (*) có 2 nghiệm trái dấu $Leftrightarrow {{m}^{2}}-9<0Leftrightarrow -3<m<3.$
TH2: (*) có 1 nghiệm bằng 0 và 1 nghiệm dương $Leftrightarrow left{ begin{matrix} {{m}^{2}}-9=0 \ m+1>0text{ } \end{matrix} right.Leftrightarrow m=3.$
Kết hợp hai trường hợp này và điều kiện $left{ begin{matrix} min mathbb{Z}text{ } \ min left[ -100;100 right] \end{matrix} right.Rightarrow $ có 6 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Chọn A.
| Ví dụ 8: Cho hàm số $y=fleft( x right)$ xác định và có đạo hàm $f’left( x right)={{x}^{3}}-left( m+3 right){{x}^{2}}+2x+4m$ trên$mathbb{R}$. Số giá trị nguyên của tham số m thuộc đoạn $left[ -100;100 right]$ để hàm số$fleft( left| x right| right)$ có 7 điểm cực trị là:
A. 100. B. 101. C. 198. D. 197. |
Lời giải
Để hàm số $fleft( left| x right| right)$ có 7 điểm cực trị thì hàm số $y=fleft( x right)$ có 3 điểm cực trị có hoành độ dương.
$Leftrightarrow f’left( x right)=0$ có 3 nghiệm dương phân biệt.
Ta có: $f’left( x right)={{x}^{3}}-left( m+3 right){{x}^{2}}+2x+4m=0Leftrightarrow {{x}^{3}}-3{{x}^{2}}+2x+mleft( 4-{{x}^{2}} right)=0$
$Leftrightarrow xleft( x-1 right)left( x-2 right)-mleft( x-2 right)left( x+2 right)=0Leftrightarrow left[ begin{matrix} x=2text{ } \ gleft( x right)={{x}^{2}}-left( m+1 right)x-2m=0 \end{matrix} right.$
Giả thiết bài toán thỏa mãn $Leftrightarrow gleft( x right)$ có 2 nghiệm dương phân biệt khác 2
$Leftrightarrow left{ begin{matrix} Delta >0text{ } \ S=m+1>0text{ } \ begin{array} {} P=2m>0 \ {} gleft( 2 right)ne 0text{ } \ end{array} \end{matrix} right.Leftrightarrow left{ begin{matrix} {{m}^{2}}+10m+1>0 \ m>0text{ } \ 2ne 0text{ } \end{matrix} right.Leftrightarrow m>0.$
Kết hợp $left{ begin{matrix} min mathbb{Z}text{ } \ min left[ -100;100 right] \end{matrix} right.Rightarrow $ có 100 giá trị nguyên của m. Chọn A.
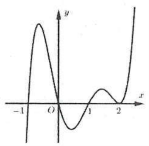
| Ví dụ 9: Cho hàm số $y=fleft( x right)$ xác định trên$mathbb{R}$và có đồ thị hình vẽ dưới. Số điểm cực trị của hàm số $fleft( left| x right|+1 right)$ là:
A. 4. B. 6. C. 5. D. 3. |
Lời giải
Ta có: $y’=left( left| x right|+1 right)’.f’left( left| x right|+1 right)=frac{x}{left| x right|}.f’left( left| x right|+1 right)=0Leftrightarrow left[ begin{matrix} x=0text{ } \ f’left( left| x right|+1 right)=0 \end{matrix} right.(*)$
Dựa vào đồ thị hàm số ta thấy $f’left( x right)=0Leftrightarrow left[ begin{matrix} x={{x}_{1}}in left( -1;0 right) \ begin{array} {} x={{x}_{2}}in left( 0;1 right)text{ } \ {} x={{x}_{3}}in left( 1;2 right) \ {} x=2text{ } \ end{array} \end{matrix} right.$
Suy ra $f’left( left| x right|+1 right)=0Leftrightarrow left[ begin{matrix} left| x right|+1={{x}_{1}}in left( -1;0 right) \ begin{array} {} left| x right|+1={{x}_{2}}in left( 0;1 right)text{ } \ {} left| x right|+1={{x}_{3}}in left( 1;2 right) \ {} left| x right|+1=2 \ end{array} \end{matrix} right.Leftrightarrow left[ begin{matrix} left| x right|+1={{x}_{3}}in left( 1;2 right) \ left| x right|+1=2text{ } \end{matrix} right.Rightarrow $hệ có 4 nghiệm.
Do đó (*) có 5 nghiệm phân biệt nên hàm số có 5 điểm cực trị. Chọn C.