1.1. Thể tích khối chóp
Thể tích của khối chóp có diện tích đáy S và chiều cao h là \(V = \frac{1}{3}hS\).
1.2. Thể tích khối chóp cụt đều
Thể tích của khối chóp cụt đều có diện tích đáy lớn S, diện tích đây bé S’ và chiều cao h là \(V = \frac{1}{3}h\left( {S + S’ + \sqrt {S.S’} } \right)\).
1.3. Thể tích khối lăng trụ
Thể tích của khối lăng trụ có diện tích đáy S và chiều cao h là V =h . S.
Câu 1:
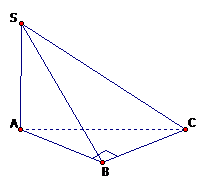
Cho hình chóp S.ABC có tam giác ABC vuông tại B, \(AB=a \sqrt 2, AC=a \sqrt 3\), cạnh bên SA vuông góc với mặt phẳng đáy và \(SB=a \sqrt 3.\) Tính thể tích khối chóp S.ABC.
Hướng dẫn giải:

Tam giác ABC vuông tại B nên \(BC = \sqrt {A{C^2} – A{B^2}} = a.\)
Suy ra: \({{\rm{S}}_{\Delta {\rm{ABC}}}} = \frac{1}{2}BA.BC = \frac{1}{2}.a\sqrt 2 .a = \frac{{{a^2}.\sqrt 2 }}{2}\)
Tam giác SAB vuông tại A có \(SA = \sqrt {S{B^2} – A{B^2}} = a.\)
Vậy thể tích khối chóp S.ABC là: \({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{{a^2}.\sqrt 2 }}{2}.a = \frac{{{a^3}.\sqrt 2 }}{6}.\)
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB=a, \(AC=a\sqrt3\), cạnh A’B = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’.
Hướng dẫn giải:
.png)
Tam giác ABC vuông tại B nên \(BC=\sqrt {A{C^2} – A{B^2}} = a\sqrt 2.\)
Suy ra: \({S_{ABC}} = \frac{1}{2}AB.BC = \frac{{{a^2}\sqrt 2 }}{2}.\)
Tam giác A’AB vuông tại A nên: \(A’A = \sqrt {A'{B^2} – A{B^2}} = a\sqrt 3 .\)
Vậy thể tích khối lăng trụ là: \({V_{ABC.A’B’C’}} = {S_{ABC}}.A’A = \frac{{{a^3}\sqrt 6 }}{2}.\)