Giải SGK Toán 11 Bài 2: Ứng dụng lôgarit vào đo lường độ pH của dung dịch – CTST – SÁCH GIÁO KHOA CHÂN TRỜI SÁNG TẠO 2023 ================ Giải bài tập Toán lớp 11 Bài 2: Ứng dụng lôgarit vào đo lường độ pH của dung dịch Thực hành 1 trang 105 Toán 11 […]
Sách giáo khoa Toán lớp 9 – tập 2 – (Kết nối)========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2023. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao […]
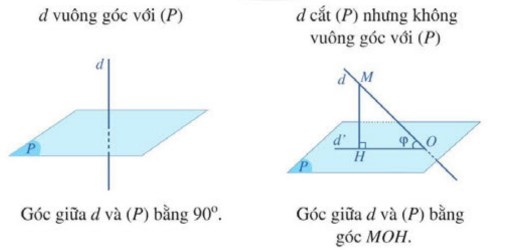
1.1. Góc giữa đường thẳng và mặt phẳng Định nghĩa Cho đường thẳng d và mặt phẳng (P), ta có: – Nếu đường thẳng d vuông góc với mặt phẳng (P) thì góc giữa d và (P) bằng \({{90}^{0}}\). – Nếu đường thẳng d không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng d và mặt phẳng (P) là góc giữa d và hình chiếu d’ […]
LÝ THUYẾT TÓM TẮT 1.1. Äá»nh nghÄ©a Hai mặt phẳng cắt nhau tạo nên bá»n góc nhá» diá»n. Nếu má»t trong các góc nhá» diá»n Äó là góc nhá» diá»n vuông thì hai mặt phẳng Äã cho gá»i là vuông góc vá»i nhau. – Khi hai mặt phẳng (P) và (Q) vuông góc vá»i nhau, ta […]
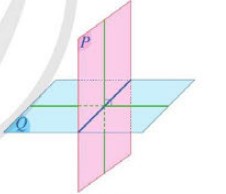
1.1. Góc giữa hai mặt phẳng, hai mặt phẳng vuông góc – Cho hai mặt phẳng (P) và (Q). Lấy các đường thẳng a, b tương ứng vuông góc với (P), (Q). Khi đó, góc giữa a và b không phụ thuộc vào vị trí của a, b và được gọi là góc giữa hai […]
1.1. Khái niệm Lôgarit Định nghĩa Cho hai số thực dương a, b với a khác 1. Số thực c để ac = b được gọi là lôgarit cơ số a của b và kí hiệu là \({{\log }_{a}}b\), nghĩa là \(c={{\log }_{a}}b\Leftrightarrow {{a}^{c}}=b\) Tính chất Với số thực dương a khác 1, số thực dương b, ta có: 1) \({{\log }_{a}}1=0\) 2) \({{\log }_{a}}a\,=1\) 3) \({{\log }_{a}}{{a}^{c}}=c\) 4) \({{a}^{{{\log }_{a}}b}}=b\) Lôgarit thập […]
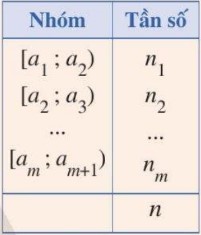
1.1. Mẫu số liệu ghép nhóm a. Bảng tần số ghép nhóm – Mẫu số liệu ghép nhóm là mẫu số liệu cho dưới dạng bảng tần số ghép nhóm. – Mỗi nhóm số liệu gồm một số giá trị của mẫu số liệu được ghép nhóm theo một tiêu chí xác định có dạng [a; b), […]
1.1. Giới hạn hữu hạn của hàm số tại một điểm a. Định nghĩa Cho khoảng K chứa điểm \(x_0\) và hàm số \(y = f(x)\) xác định trên \(K\) hoặc trên \(K\setminus \{x_0\}\). Hàm số \(f(x)\) có giới hạn là số L khi x dần tới \(x_0\) nếu với dãy số (\(x_n\) bất kì, \(x_n\in K\setminus \{x_0\}\) và \(x_n \to x_0\), thì \(f(x_n) \to L\). Kí […]
LÝ THUYẾT TÓM TẮT 1.1. Cấp sá» nhân Cấp sá» nhân là má»t dãy sá» (hữu hạn hay vô hạn) mà trong Äó ká» từ sá» hạng thứ hai, má»i sá» hạng Äá»u là tÃch của sá» hạng Äứng ngay trÆ°á»c nó vá»i má»t sá» q không Äá»i. un+1 = un .q vá»i \(n\in N*\). Sá» q Äược gá»i là công bá»i của cấp sá» […]
LÝ THUYẾT TÓM TẮT 1.1. Khái niá»m phÆ°Æ¡ng trình tÆ°Æ¡ng ÄÆ°Æ¡ng – Hai phÆ°Æ¡ng trình Äược gá»i là tÆ°Æ¡ng ÄÆ°Æ¡ng khi chúng có cùng táºp nghiá»m. – Nếu phÆ°Æ¡ng trình f(x)=0 tÆ°Æ¡ng ÄÆ°Æ¡ng vá»i phÆ°Æ¡ng trình g(x)= 0 thì ta viết f(x)=0 \( \Leftrightarrow \) g(x)=0. Chú ý. Hai phÆ°Æ¡ng trình vô nghiá»m là tÆ°Æ¡ng ÄÆ°Æ¡ng. 1.2. […]