BÀI TẬP TÌM GIÁ TRỊ NHỎ NHẤT – GIÁ TRỊ LỚN NHẤT CỦA HÀM SỐ CÓ ĐÁP ÁN
Dưới đây là bài tập tìm GTLN – GTNN của hàm số có đáp án
| Bài tập 1: Giá trị nhỏ nhất của hàm số $y={{x}^{3}}-3x+5$ trên đoạn [0;2] là
A. 0. B. 3. C. 5. D. 7. |
Lời giải chi tiết
Đáp án: Chọn B
Xét hàm số $f(x)={{x}^{3}}-3x+5$ trên [0;2], có $f'(x)=3{{x}^{2}}-3$
Phương trình $f'(x)=0Leftrightarrow left{ begin{array} {} 0le xle 2 \ {} 3{{x}^{2}}-3=0 \ end{array} right.Leftrightarrow x=1$
Tính $f(0)=5;f(1)=3;f(2)=7.$ Vậy $underset{text{ }!![!!text{ }0;2]}{mathop{min }},f(x)=f(1)=3$.
| Bài tập 2: Giá trị lớn nhất của hàm số $f(x)={{x}^{4}}-2{{x}^{2}}+1$ trên đoạn [0;2] là
A. 64. B. 1. C. 0. D. 9. |
Lời giải chi tiết
Đáp án: Chọn D
Xét hàm số $f(x)={{x}^{4}}-2{{x}^{2}}+1$ trên [0;2], có $f'(x)=4{{x}^{3}}-4x$
Phương trình $f'(x)=0Leftrightarrow left{ begin{array} {} 0le xle 2 \ {} 4{{x}^{3}}-4x=0 \ end{array} right.Leftrightarrow left[ begin{array} {} x=0 \ {} x=1 \ end{array} right.$
Tính $f(0)=1;f(1)=0;f(2)=9.$ Vậy $underset{text{ }!![!!text{ }0;2]}{mathop{max }},f(x)=f(2)=9.$
| Bài tập 3: Giá trị nhỏ nhất của hàm số $f(x)=frac{{{x}^{2}}+3}{x-1}$ trên đoạn [2;4] là
A. 7. B. 6. C. $frac{19}{3}$ D. $frac{13}{3}.$ |
Lời giải chi tiết
Đáp án: Chọn B
Cần nhớ công thức đạo hàm: ${{left( frac{u}{v} right)}^{‘}}=frac{u’v-uv’}{{{v}^{2}}}$
Cách 1: Xét hàm số $f(x)=frac{{{x}^{2}}+3}{x-1}$ trên [2;4], có $f'(x)=frac{{{x}^{2}}-2x-3}{{{(x-1)}^{2}}}$
Phương trình $f'(x)=0Leftrightarrow left{ begin{array} {} 2le xle 4 \ {} {{x}^{2}}-2x-3=0 \ end{array} right.Leftrightarrow x=3$
Tính $f(2)=7;f(3)=6;f(4)=frac{19}{3}.$ Vậy $underset{text{ }!![!!text{ 2;4 }!!]!!text{ }}{mathop{min }},f(x)=f(3)=6$.
Cách 2: Sử dụng công cụ TABLE (MODE 7)
Bước 1: Bấm tổ hợp phím MODE 7
Bước 2: Nhập $f(X)=frac{{{X}^{2}}+3}{X-1}$
Sau đó ấn phím = (nếu có $g(X)$ thì ấn tiếp phím =) sau đó nhập $left{ begin{array} {} Star=2 \ {} End=4 \ {} Step=0.2 \ end{array} right.$
(Chú ý: Thường ta chọn $Step=frac{End-Start}{10}$)
Bước 3: Tra bảng nhận được và tìm GTNN:
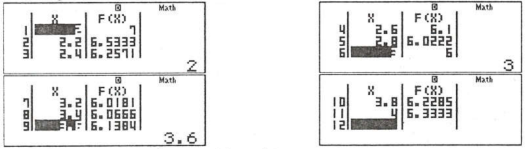
Dựa vào bảng giá trị ở trên, ta thấy $underset{text{ }!![!!text{ }2;4]}{mathop{min }},f(x)=f(3)=6.$
| Bài tập 4: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $f(x)=frac{3x-1}{x-3}$ trên đoạn [0;2]. Giá trị của 3M + m bằng
A. 0. B. – 4. C. – 2. D. 1. |
Lời giải chi tiết
Đáp án: Chọn C
Xét hàm số $f(x)=frac{3x-1}{x-3}$trên [0;2] có $f'(x)=-frac{8}{{{(x-3)}^{2}}}<0$
Suy ra $f(x)$ là hàm số nghịch biến trên (0;2) $Rightarrow left{ begin{array} {} underset{text{ }!![!!text{ 0;2 }!!]!!text{ }}{mathop{min }},f(x)=f(2)=-5 \ {} underset{text{ }!![!!text{ 0;2 }!!]!!text{ }}{mathop{max }},f(x)=f(0)=frac{1}{3} \ end{array} right.$
Vậy $M=frac{1}{3}Rightarrow 3M=3;m=-5to 3M+m=-2$
| Bài tập 5: Giá trị lớn nhất của hàm số $y=sqrt{3x-2x-{{x}^{2}}}$ là
A. 1. B. 2. C. 3. D. 4. |
Lời giải chi tiết
Đáp án: Chọn B
Cần nhớ công thức đạo hàm: ${{left( sqrt{u} right)}^{‘}}=frac{u’}{2sqrt{u}}$
Điều kiện xác định: $3-2x-{{x}^{2}}ge 0Leftrightarrow -3le xle 1$
Xét hàm số $f(x)=sqrt{3-2x-{{x}^{2}}}$ trên [-3;1], có $f'(x)=frac{-2-2x}{2sqrt{3-2x-{{x}^{2}}}}=-frac{x+1}{sqrt{3-2x-{{x}^{2}}}};$
Phương trình $f'(x)=0Leftrightarrow left{ begin{array} {} -3<x<1 \ {} x+1=0 \ end{array} right.Leftrightarrow x=-1$
Tính $f(-3)=0;f(-1)=2;f(1)=0.$ Vậy $underset{text{ }!![!!text{ }-3;1]}{mathop{max}},f(x)=f(-1)=2.$
| Bài tập 6: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=xsqrt{1-{{x}^{2}}}.$ Giá trị của
M – 2m bằng A. 0. B. $-frac{1}{2}.$ C. 1. D. $frac{3}{2}.$ |
Lời giải chi tiết
Đáp án: Chọn D
Điều kiện xác định: $1-{{x}^{2}}ge 0Leftrightarrow -1le xle 1$
Xét hàm số $f(x)=xsqrt{1-{{x}^{2}}}$ trên [-1;1], có $f'(x)=sqrt{1-{{x}^{2}}}-frac{{{x}^{2}}}{sqrt{1-{{x}^{2}}}}=frac{1-2{{x}^{2}}}{sqrt{1-{{x}^{2}}}}$
Phương trình $f'(x)=0Leftrightarrow left{ begin{array} {} -1<x<1 \ {} 1-2{{x}^{2}}=0 \
end{array} right.Leftrightarrow x=left{ -frac{sqrt{2}}{2};frac{sqrt{2}}{2} right}$
Tính $f(-1)=f(1)=0;fleft( -frac{sqrt{2}}{2} right)=-frac{1}{2};fleft( -frac{sqrt{2}}{2} right)=frac{1}{2}$
Vậy $left{ begin{array} {} m=underset{text{ }!![!!text{ }-1;1]}{mathop{min }},f(x)=-frac{1}{2} \ {} M=underset{text{ }!![!!text{ }-1;1]}{mathop{max }},f(x)=frac{1}{2} \ end{array} right.to M-2m=frac{1}{2}-2.left( -frac{1}{2} right)=frac{3}{2}$
| Bài tập 7: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=sqrt{1-x}+sqrt{1+x}$. Giá trị của $M-2{{m}^{2}}$ bằng
A. – 2. B. 2. C. 0. D. – 1. |
Lời giải chi tiết
Đáp án: Chọn A
Điều kiện xác định: $left{ begin{array} {} 1-xge 0 \ {} x+1ge 0 \ end{array} right.Leftrightarrow -1le xle 1$
Xét hàm số $f(x)=sqrt{1-x}+sqrt{1+x}$ trên [-1;1], có $f'(x)=-frac{1}{2sqrt{1-x}}+frac{1}{2sqrt{1+x}};$
Phương trình $f'(x)=0Leftrightarrow left{ begin{array} {} -1<x<1 \ {} sqrt{1-x}=sqrt{1-x} \ end{array} right.Leftrightarrow x=0$. Tính $f(-1)=f(1)=sqrt{2};f(0)=2$
Vậy $left{ begin{array} {} m=underset{text{ }!![!!text{ }-1;1]}{mathop{min }},f(x)=sqrt{2} \ {} M=underset{text{ }!![!!text{ }-1;1]}{mathop{max }},f(x)=2 \ end{array} right.to M-2{{m}^{2}}=2-2.2=-2$
| Bài tập 8: Giá trị lớn nhất của hàm số $y=sqrt{x-1}+sqrt{3-x}-2sqrt{-{{x}^{2}}+4x-3}$ là
A. 0. B. $-sqrt{2}.$ C. $sqrt{2}.$ D. $frac{9}{4}.$ |
Lời giải chi tiết
Đáp án: Chọn C
Điều kiện xác định: $left{ begin{array} {} x-1ge 0 \ {} 3-xge 0 \ end{array} right.Leftrightarrow 1le xle 3$
Đặt $t=sqrt{x-1}+sqrt{3-x},$ ta có $t’=frac{1}{2sqrt{x-1}}-frac{1}{sqrt{3-x}};,t’=0Leftrightarrow x=2$
Tính $t(1)=t(3)=sqrt{2};t(2)=2xrightarrow{{}}sqrt{2}le tle 2$
Khi đó ${{t}^{2}}=2+2sqrt{(x-1)(3-x)}=2+2sqrt{-{{x}^{2}}+4x-3}Leftrightarrow 2sqrt{-{{x}^{2}}+4x-3}={{t}^{2}}-2$
Do đó $y=f(t)=t-({{t}^{2}}-2)=-{{t}^{2}}+t+2$
Xét $f(t)=-{{t}^{2}}+t+2$ trên $left[ sqrt{2};2 right]xrightarrow{{}}underset{text{ }!![!!text{ }sqrt{2};2]}{mathop{max }},f(t)=sqrt{2}.$ Vậy $underset{text{ }!![!!text{ }1;3]}{mathop{max }},y=sqrt{2}$
| Bài tập 9: Giá trị nhỏ nhất của hàm số $y=2{{cos }^{3}}x-frac{9}{2}{{cos }^{2}}x+3cos x+frac{1}{2}$ là
A. – 9. B. 1. C. $-frac{3}{2}.$ D. $frac{1}{2}.$ |
Lời giải chi tiết
Đáp án: Chọn B
Đặt $t=cos xin text{ }!![!!text{ }-1;1],$ khi đó $y=f(t)=2{{t}^{3}}-frac{9}{2}{{t}^{2}}+3t+frac{1}{2}$
Xét hàm số $f(t)=2{{t}^{3}}-frac{9}{2}{{t}^{2}}+3t+frac{1}{2}$ trên [-1;1], có $f'(t)=8{{t}^{2}}-9t+3>0,forall t$
Suy ra $f(t)$ là hàm số đồng biến trên $(-1;1)Rightarrow underset{text{ }!![!!text{ }-1;1]}{mathop{min }},f(t)=f(-1)=1.$
| Bài tập 10: Giá trị lớn nhất của hàm số $y={{sin }^{3}}x+cos 2x+sin x+3$ là
A. 0. B. 5. C. 4. D. $frac{112}{27}.$ |
Lời giải chi tiết
Đáp án: Chọn D
Cần nhớ công thức lượng giác: $cos 2x=1-2{{sin }^{2}}x$
Ta có $y={{sin }^{3}}x+1-2{{sin }^{2}}x+sin x+3={{sin }^{3}}x-2{{sin }^{2}}x+sin x+4$
Đặt $t=sin xin text{ }!![!!text{ }-1;1],$ khi đó $y=f(t)={{t}^{3}}-2{{t}^{2}}+t+4$
Xét hàm số $f(t)={{t}^{3}}-2{{t}^{2}}+t+4$ trên [-1;1], có $f'(t)=3{{t}^{2}}-4t+1;$
Phương trình $f'(t)=0Leftrightarrow left{ begin{array} {} -1le tle 1 \ {} 3{{t}^{2}}-4t+1=0 \ end{array} right.Leftrightarrow left[ begin{array} {} t=1 \ {} t=frac{1}{3} \ end{array} right.$
Tính $f(-1)=0;fleft( frac{1}{3} right)=frac{112}{27};f(1)=4.$ Vậy ${{y}_{max }}=frac{112}{27}.$
| Bài tập 11: Tìm giá trị lớn nhất M của hàm số $f(x)=left| -{{x}^{2}}-4x+5 right|$ trên đoạn [-6;6]
A. 110. B. 9. C. 55. D. 7. |
Lời giải chi tiết
Đáp án: Chọn C
Xét hàm số $g(x)=-{{x}^{2}}-4x+5$ liên tục trên đoạn [-6;6]
Đạo hàm $g'(x)=-2x-4to g'(x)=0Leftrightarrow x=-2in text{ }!![!!text{ }-6;6]$
Lại có $g(x)=0Leftrightarrow -{{x}^{2}}-4x+5=0Leftrightarrow left[ begin{array} {} x=1in text{ }!![!!text{ }-6;6] \ {} x=-5in text{ }!![!!text{ }-6;6] \ end{array} right.$
Tính $left{ begin{array} {} g(-6)=-7 \ {} g(-2)=9 \ {} g(6)=-55 \ {} g(1)=g(-5)=0 \ end{array} right.to underset{text{ }!![!!text{ }-6;6]}{mathop{max }},f(x)=underset{text{ }!![!!text{ }-6;6]}{mathop{max }},left{ left| g(-6) right|;left| g(-2) right|;left| g(6) right|;left| g(1) right|;left| g(-5) right| right}=55.$
Nhận xét: bài này rất dễ sai lầm vì không để ý hàm trị tuyệt đối không âm.
| Bài tập 12: Tìm giá trị lớn nhất M của hàm số $f(x)=left| {{x}^{2}}-3x+2 right|-x$ trên đoạn [-4;4]
A. 2. B. 17. C. 34. D. 68. |
Lời giải chi tiết
Đáp án: Chọn C
Hàm số $f(x)$ xác định và liên tục trên đoạn [-4;4]
- Nếu $xin text{ }!![!!text{ }1;2]$ thì ${{x}^{2}}-3x+2le 0$ nên suy ra $f(x)=-{{x}^{2}}+2x-2$
Đạo hàm $f'(x)=-2x+2to f'(x)=0Leftrightarrow x=1in text{ }!![!!text{ }1;2].$ Ta có $left{ begin{array} {} f(1)=-1 \ {} f(2)=-2 \ end{array} right.$
- Nếu $xin text{ }!![!!text{ }-4;1]cup text{ }!![!!text{ }2;4]$ thì ${{x}^{2}}-3x+2ge 0$ nên suy ra $f(x)={{x}^{2}}-4x+2$
Đạo hàm $f'(x)=2x-4to f'(x)=0Leftrightarrow x=2in text{ }!![!!text{ }-4;1]cup text{ }!![!!text{ }2;4].$ Ta có $left{ begin{array} {} f(-4)=34 \ {} f(1)=-1 \ {} f(2)=-2 \ {} f(4)=2 \ end{array} right.$
So sánh hai trường hợp, ta được $underset{text{ }!![!!text{ }-4;4]}{mathop{max }},f(x)=f(-4)=34.$
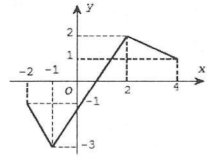
| Bài tập 13: Cho hàm số $y=f(x)$ có đồ thị trên đoạn [-2;4] như hình vẽ. Tìm giá trị lớn nhất M của hàm số $y=left| f(x) right|$ trên đoạn [-2;4]?
A. 2. B. 3. C. 1. D. $left| f(0) right|.$ |
Lời giải chi tiết
Đáp án: Chọn B
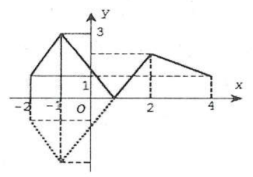
| Từ đồ thị hàm số $y=f(x)$ trên đoạn [-2;4]
Ta suy ra đồ thị hàm số $left| f(x) right|$ trên [-2;4] như hình vẽ. Do đó $underset{text{ }!![!!text{ }-2;4]}{mathop{max }},left| f(x) right|=3$ tại $x=-1$ |
 |
| Bài tập 14: Cho $(P):y={{x}^{2}}$ và $Aleft( -2;frac{1}{2} right)$. Gọi M là điểm bất kì thuộc (P). Khoảng cách MA bé nhất là
A. $frac{5}{4}.$ B. $frac{2sqrt{3}}{3}.$ C. $frac{sqrt{2}}{2}.$ D. $frac{sqrt{5}}{2}.$ |
Lời giải chi tiết
Đáp án: Chọn D
Vì M thuộc parabol (P) $Rightarrow M(m;{{m}^{2}})Rightarrow overrightarrow{AM}=left( m+2;{{m}^{2}}-frac{1}{2} right)$
Suy ra $M{{A}^{2}}={{left| overline{AM} right|}^{2}}={{(m+2)}^{2}}+{{left( m-frac{1}{2} right)}^{2}}={{m}^{4}}+4m+frac{17}{4}$
Xét hàm số $f(m)={{m}^{4}}+4m+frac{17}{4},$ có $f'(m)=4{{m}^{3}}+4;f'(m)=0Leftrightarrow m=-1$
Do đó $min f(m)=f(-1)=1-4+frac{17}{4}=frac{5}{4}to M{{A}_{min }}=sqrt{frac{5}{4}}=frac{sqrt{5}}{2}.$
| Bài tập 15: Cho hai hàm số $y=f(x),y=g(x)$ liên tục và có đạo hàm trên đoạn [-1;1] thỏa mãn $f(x)>0,g(x)>0,forall xin text{ }!![!!text{ }-1;1]$ và $f'(x)ge g'(x)ge 0,forall xin text{ }!![!!text{ }-1;1].$ Gọi m là giá trị nhỏ nhất trên đoạn [-1;1] của hàm số $h(x)=2f(x).g(x)-{{g}^{2}}(x).$ Mệnh đề nào dưới đây đúng?
A. $m=h(-1).$ B. $m=h(0).$ C. $m=frac{h(-1)+h(1)}{2}.$ D. $m=h(1).$ |
Lời giải chi tiết
Đáp án: Chọn A
Ta có $h'(x)=2.left[ f'(x).g(x)+f(x).g'(x) right]-2g'(x).g(x);,,forall xin text{ }!![!!text{ }-1;1]$
Suy ra $h(x)=2.g(x).left[ f'(x)-g'(x) right]+2f(x).g'(x)ge 0$ vì $f'(x)-g'(x)ge 0$
Do đó $h(x)$ là hàm số đồng biến trên [-1;1] $Rightarrow underset{text{ }!![!!text{ }-1;1]}{mathop{min }},h(x)=h(-1).$