adsense
Giải bài tập Bài 11: Tích vô hướng của hai vectơ (Kết nối)
===============
Giải bài 4.21 trang 70 SGK Toán 10 Kết nối tri thức tập 1
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ (overrightarrow a ) và (overrightarrow b ) trong mỗi trường hợp sau:
a) (overrightarrow a = ( – 3;1),;overrightarrow b = (2;6))
b) (overrightarrow a = (3;1),;overrightarrow b = (2;4))
c) (overrightarrow a = ( – sqrt 2 ;1),;overrightarrow b = (2; – sqrt 2 ))
Phương pháp giải
Tính góc giữa hai vectơ dựa vào tích vô hướng: (cos left( {overrightarrow a ,overrightarrow b } right) = frac{{overrightarrow a .overrightarrow b }}{{left| {overrightarrow a } right|.left| {overrightarrow b } right|}})
Hướng dẫn giải
a)
(overrightarrow a .overrightarrow b = ( – 3).2 + 1.6 = 0)
( Rightarrow overrightarrow a bot overrightarrow b ) hay (left( {overrightarrow a ,overrightarrow b } right) = {90^o}).
b)
(left{ begin{array}{l}overrightarrow a .overrightarrow b = 3.2 + 1.4 = 10\|overrightarrow a |, = sqrt {{3^2} + {1^2}} = sqrt {10} ;;,|overrightarrow b |, = sqrt {{2^2} + {4^2}} = 2sqrt 5 end{array} right.)
(begin{array}{l} Rightarrow cos left( {overrightarrow a ,overrightarrow b } right) = frac{{10}}{{sqrt {10} .2sqrt 5 }} = frac{{sqrt 2 }}{2}\ Rightarrow left( {overrightarrow a ,overrightarrow b } right) = {45^o}end{array})
c) Dễ thấy: (overrightarrow a ) và (overrightarrow b ) cùng phương do (frac{{ – sqrt 2 }}{2} = frac{1}{{ – sqrt 2 }})
Hơn nữa: (overrightarrow b = left( {2; – sqrt 2 } right) = – sqrt 2 .left( { – sqrt 2 ;1} right) = – sqrt 2 .overrightarrow a ;); ( – sqrt 2 < 0)
Do đó: (overrightarrow a ) và (overrightarrow b ) ngược hướng.
( Rightarrow left( {overrightarrow a ,overrightarrow b } right) = {180^o})
Chú ý:
Khi tính góc, ta kiểm tra các trường hợp dưới đây trước:
+ (left( {overrightarrow a ,overrightarrow b } right) = {90^o}): nếu (overrightarrow a .overrightarrow b = 0)
+ (overrightarrow a ) và (overrightarrow b ) cùng phương:
(left( {overrightarrow a ,overrightarrow b } right) = {0^o}) nếu (overrightarrow a ) và (overrightarrow b ) cùng hướng
(left( {overrightarrow a ,overrightarrow b } right) = {0^o}) nếu (overrightarrow a ) và (overrightarrow b ) ngược hướng
Nếu không thuộc các trường hợp trên thì ta tính góc dựa vào công thức (cos left( {overrightarrow a ,overrightarrow b } right) = frac{{overrightarrow a .overrightarrow b }}{{left| {overrightarrow a } right|.left| {overrightarrow b } right|}}).
Giải bài 4.22 trang 70 SGK Toán 10 Kết nối tri thức tập 1
Tìm điều kiện của (overrightarrow u ,;overrightarrow v ) để:
a) (overrightarrow u .;overrightarrow v = left| {overrightarrow u } right|.;left| {overrightarrow v } right|)
b) (overrightarrow u .;overrightarrow v = – left| {overrightarrow u } right|.;left| {overrightarrow v } right|)
Phương pháp giải
Tích vô hướng (overrightarrow u .;overrightarrow v = left| {overrightarrow u } right|.;left| {overrightarrow v } right|.cos left( {overrightarrow u ,;overrightarrow v } right))
Hướng dẫn giải
a)
Ta có: (overrightarrow u .;overrightarrow v = left| {overrightarrow u } right|.;left| {overrightarrow v } right|.cos left( {overrightarrow u ,;overrightarrow v } right) = left| {overrightarrow u } right|.;left| {overrightarrow v } right|)
( Rightarrow cos left( {overrightarrow u ,;overrightarrow v } right) = 1 Leftrightarrow left( {overrightarrow u ,;overrightarrow v } right) = {0^o})
Nói cách khác: (overrightarrow u ,;overrightarrow v ) cùng hướng.
b)
Ta có: (overrightarrow u .;overrightarrow v = left| {overrightarrow u } right|.;left| {overrightarrow v } right|.cos left( {overrightarrow u ,;overrightarrow v } right) =- left| {overrightarrow u } right|.;left| {overrightarrow v } right|)
( Rightarrow cos left( {overrightarrow u ,;overrightarrow v } right) = – 1 Leftrightarrow left( {overrightarrow u ,;overrightarrow v } right) = {180^o})
Nói cách khác: (overrightarrow u ,;overrightarrow v ) ngược hướng.
Giải bài 4.23 trang 70 SGK Toán 10 Kết nối tri thức tập 1
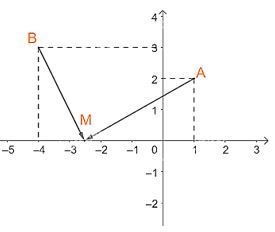
Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2), B(-4; 3). Gọi M (t; 0) là một điểm thuộc trục hoành.
a) Tính (overrightarrow {AM} .overrightarrow {BM} ) theo t.
b) Tính t để (widehat {AMB} = {90^o})
Phương pháp giải
+) Nếu vecto (overrightarrow {AM} (x;y)) và (overrightarrow {BM} (a;b)) thì (overrightarrow {AM} .overrightarrow {BM} = xa + yb)
+) (widehat {AMB} = {90^o} Leftrightarrow AM bot BM)
Hướng dẫn giải
a)
Ta có: A (1; 2), B(-4; 3) và M (t; 0)
(begin{array}{l}
Rightarrow overrightarrow {AM} = (t – 1; – 2),;overrightarrow {BM} = (t + 4; – 3)\
Rightarrow overrightarrow {AM} .overrightarrow {BM} = (t – 1)(t + 4) + ( – 2)( – 3)\
quad quad quad quad quad quad= {t^2} + 3t + 2.
end{array})
b)
Để (widehat {AMB} = {90^o}) hay (AM bot BM) thì (overrightarrow {AM} .overrightarrow {BM} = 0)
adsense
(begin{array}{l} Leftrightarrow {t^2} + 3t + 2 = 0\ Leftrightarrow left[ begin{array}{l}t = – 1\t = – 2end{array} right.end{array})
Vậy t = -1 hoặc t = -2 thì (widehat {AMB} = {90^o})
Giải bài 4.24 trang 70 SGK Toán 10 Kết nối tri thức tập 1
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A (-4; 1), B (2;4), C (2; -2)
a) Giải tam giác
b) Tìm tọa độ trực tâm H của tam giác ABC.
Phương pháp giải
a) Độ dài vectơ (overrightarrow {AB} (x;y)) là (left| {overrightarrow {AB} } right| = sqrt {{x^2} + {y^2}} )
b) Chỉ ra (overrightarrow {AH} .overrightarrow {BC} = overrightarrow 0 ) và (overrightarrow {BH} .overrightarrow {CA} = overrightarrow 0 ) từ đó tìm tọa độ của H.
Hướng dẫn giải
a) Ta có:
(left{ begin{array}{l}overrightarrow {AB} = (2 – ( – 4);4 – 1) = (6;3)\overrightarrow {BC} = (2 – 2; – 2 – 4) = (0; – 6)\overrightarrow {AC} = (2 – ( – 4); – 2 – 1) = (6; – 3)end{array} right.)( Rightarrow left{ begin{array}{l}AB = left| {overrightarrow {AB} } right| = sqrt {{6^2} + {3^2}} = 3sqrt 5 \BC = left| {overrightarrow {BC} } right| = sqrt {{0^2} + {{( – 6)}^2}} = 6\AC = left| {overrightarrow {CA} } right| = sqrt {{6^2} + {{( – 3)}^2}} = 3sqrt 5 .end{array} right.)
Áp dụng định lí cosin cho tam giác ABC, ta có:
(cos widehat A = frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = frac{{{{left( {3sqrt 5 } right)}^2} + {{left( {3sqrt 5 } right)}^2} – {{left( 6 right)}^2}}}{{2.3sqrt 5 .3sqrt 5 }} = frac{3}{5})( Rightarrow widehat A approx 53,{13^o})
(cos widehat B = frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} = frac{{{{left( 6 right)}^2} + {{left( {3sqrt 5 } right)}^2} – {{left( {3sqrt 5 } right)}^2}}}{{2.6.3sqrt 5 }} = frac{{sqrt 5 }}{5})( Rightarrow widehat B approx 63,{435^o})
( Rightarrow widehat C approx 63,{435^o})
Vậy tam giác ABC có: (a = 6;b = 3sqrt 5 ;c = 3sqrt 5 ); (widehat A approx 53,{13^o};widehat B = widehat C approx 63,{435^o}.)
b)
Gọi H có tọa độ (x; y)
( Rightarrow left{ begin{array}{l}overrightarrow {AH} = (x – ( – 4);y – 1) = (x + 4;y – 1)\overrightarrow {BH} = (x – 2;y – 4)end{array} right.)
Lại có: H là trực tâm tam giác ABC
( Rightarrow AH bot BC) và (BH bot AC)
( Rightarrow left( {overrightarrow {AH} ,overrightarrow {BC} } right) = {90^o} Leftrightarrow cos left( {overrightarrow {AH} ,overrightarrow {BC} } right) = 0) và (left( {overrightarrow {BH} ,overrightarrow {AC} } right) = {90^o} Leftrightarrow cos left( {overrightarrow {BH} ,overrightarrow {AC} } right) = 0)
Do đó (overrightarrow {AH} .overrightarrow {BC} = overrightarrow 0 ) và (overrightarrow {BH} .overrightarrow {AC} = overrightarrow 0 ).
Mà: (overrightarrow {BC} = (0; – 6))
( Rightarrow (x + 4).0 + (y – 1).( – 6) = 0 Leftrightarrow – 6.(y – 1) = 0 Leftrightarrow y = 1.)
Và (overrightarrow {AC} = (6; – 3))
(begin{array}{l} Rightarrow (x – 2).6 + (y – 4).( – 3) = 0\ Leftrightarrow 6x – 12 + ( – 3).( – 3) = 0\ Leftrightarrow 6x – 3 = 0\ Leftrightarrow x = frac{1}{2}.end{array})
Vậy H có tọa độ (left( {1;frac{1}{2}} right))
Giải bài 4.25 trang 70 SGK Toán 10 Kết nối tri thức tập 1
Chứng minh rằng với mọi tam giác ABC, ta có:
({S_{ABC}} = frac{1}{2}sqrt {{{overrightarrow {AB} }^2}.{{overrightarrow {AC} }^2} – {{left( {overrightarrow {AB} .overrightarrow {AC} } right)}^2}} .)
Phương pháp giải
Biến đổi vế trái, đưa về công thức ({S_{ABC}} = dfrac{1}{2}bc.sin A)
+) (overrightarrow {AB} .overrightarrow {AC} = AB.AC.cos left( {overrightarrow {AB} ,overrightarrow {AC} } right))
+) ({sin ^2}alpha = 1 – {cos ^2}alpha ) với mọi (alpha ).
Hướng dẫn giải
Đặt (A = dfrac{1}{2}sqrt {{{overrightarrow {AB} }^2}.{{overrightarrow {AC} }^2} – {{left( {overrightarrow {AB} .overrightarrow {AC} } right)}^2}} )
(begin{array}{l} Rightarrow A = dfrac{1}{2}sqrt {A{B^2}.A{C^2} – {{left( {AB.AC.cos A} right)}^2}} \ Leftrightarrow A = dfrac{1}{2}sqrt {A{B^2}.A{C^2}left( {1 – {{cos }^2}A} right)} end{array})
Mà (1 – {cos ^2}A = {sin ^2}A)
( Rightarrow A = dfrac{1}{2}sqrt {A{B^2}.A{C^2}.{{sin }^2}A} )
( Leftrightarrow A = dfrac{1}{2}.AB.AC.sin A) (Vì ({0^o} < widehat A < {180^o}) nên (sin A > 0))
Do đó (A = {S_{ABC}}) hay ({S_{ABC}} = dfrac{1}{2}sqrt {{{overrightarrow {AB} }^2}.{{overrightarrow {AC} }^2} – {{left( {overrightarrow {AB} .overrightarrow {AC} } right)}^2}} .) (đpcm)
Giải bài 4.26 trang 70 SGK Toán 10 Kết nối tri thức tập 1
Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có:
(M{A^2} + M{B^2} + M{C^2} = 3M{G^2} + G{A^2} + G{B^2} + G{C^2})
Phương pháp giải
+) (M{A^2} = {overrightarrow {MA} ^2})
+) Với 3 điểm M, A, G bất kì ta có: (overrightarrow {MG} + overrightarrow {GA} = overrightarrow {MA} )
+) G là trọng tâm tam giác ABC thì: (overrightarrow {GA} + overrightarrow {GB} + overrightarrow {GC} = overrightarrow 0 )
Hướng dẫn giải
Ta có:
(begin{array}{l}M{A^2} + M{B^2} + M{C^2} = {overrightarrow {MA} ^2} + {overrightarrow {MB} ^2} + {overrightarrow {MC} ^2}\ = {left( {overrightarrow {MG} + overrightarrow {GA} } right)^2} + {left( {overrightarrow {MG} + overrightarrow {GB} } right)^2} + {left( {overrightarrow {MG} + overrightarrow {GC} } right)^2}\ = {overrightarrow {MG} ^2} + 2overrightarrow {MG} .overrightarrow {GA} + {overrightarrow {GA} ^2} + {overrightarrow {MG} ^2} + 2overrightarrow {MG} .overrightarrow {GB} + {overrightarrow {GB} ^2} + {overrightarrow {MG} ^2} + 2overrightarrow {MG} .overrightarrow {GC} + {overrightarrow {GC} ^2}\ = 3{overrightarrow {MG} ^2} + 2overrightarrow {MG} .left( {overrightarrow {GA} + overrightarrow {GB} + overrightarrow {GC} } right) + {overrightarrow {GA} ^2} + {overrightarrow {GB} ^2} + {overrightarrow {GC} ^2}\ = 3{overrightarrow {MG} ^2} + 2overrightarrow {MG} .overrightarrow 0 + {overrightarrow {GA} ^2} + {overrightarrow {GB} ^2} + {overrightarrow {GC} ^2}end{array})
( do G là trọng tâm tam giác ABC)
(begin{array}{l} = 3{overrightarrow {MG} ^2} + {overrightarrow {GA} ^2} + {overrightarrow {GB} ^2} + {overrightarrow {GC} ^2}\ = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}end{array}) (đpcm).
