adsense
Giải bài tập Bài 6: Hệ thức lượng trong tam giác (Kết nối)
==========
Giải bài 3.5 trang 42 SGK Toán 10 Kết nối tri thức tập 1
Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r.
Giải bài 3.5 trang 42 SGK Toán 10 Kết nối tri thức tập 1
Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r.
Phương pháp giải
Bước 1: Tính cos A bằng công thức: (cos A = frac{{{b^2} + {c^2} – {a^2}}}{{2bc}})
Bước 2: Tính S bằng công thức Herong: (S = sqrt {pleft( {p – a} right)left( {p – b} right)left( {p – c} right)} ) với (p = frac{{a + b + c}}{2})
Bước 3: Tính r bằng công thức (S = pr).
Hướng dẫn giải
Từ định lí cosin ta suy ra (cos A = frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = frac{{{5^2} + {8^2} – {6^2}}}{{2.5.8}} = frac{{53}}{{80}})
Tam giác ABC có nửa chu vi là:(p = frac{{a + b + c}}{2} = frac{{6 + 5 + 8}}{2} = 9,5.)
Theo công thức Herong ta có: (S = sqrt {pleft( {p – a} right)left( {p – b} right)left( {p – c} right)} = sqrt {9,5.left( {9,5 – 6} right).left( {9,5 – 5} right).left( {9,5 – 8} right)} approx 14,98)
Lại có: (S = pr Rightarrow r = frac{S}{p} = frac{{14,98}}{{9,5}} = 1,577.)
Vậy (cos A = frac{{53}}{{80}}); (S approx 14,98) và (r = 1,577.)
adsense
b) Tính chiều cao của tòa nhà.
Giải bài 3.9 trang 43 SGK Toán 10 Kết nối tri thức tập 1
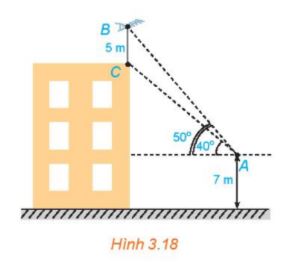
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là ({50^o})và ({40^o}) so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.

Phương pháp giải
a)
Nhắc lại: Tổng ba góc của một tam giác luôn bằng ({180^o}).
Bước 1: Gọi H là hình chiếu của A lên đường thẳng BC.
Bước 2: Tính góc (widehat {BAC}), góc (widehat {ABC}) => góc (widehat {BCA}).
b)
Bước 1: Tính AB: (AB = frac{{BC.sin C}}{{sin A}})
Bước 2: Tính BH => chiều cao của tòa nhà = BH + độ cao của
Hướng dẫn giải
a)
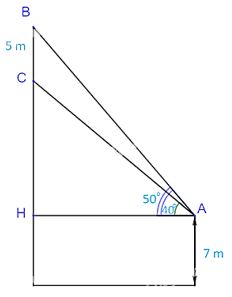
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: (widehat {HAB} = {50^o}); (widehat {HAC} = {40^o})
( Rightarrow widehat {BAC} = {50^o} – {40^o} = {10^o}) (1)
Xét tam giác ABH, vuông tại H ta có:
(widehat H = {90^o};;widehat {BAH} = {50^o}.)
( Rightarrow widehat {HBA} = {180^o} – {90^o} – {50^o} = {40^o}) hay (widehat {CBA} = {40^o}). (2)
Từ (1) và (2), suy ra: (widehat {BCA} = {180^o} – {40^o} – {10^o} = {130^o}.)
Vậy ba góc của tam giác ABC lần lượt là: (widehat A = {10^o};;widehat B = {40^o};;widehat C = {130^o}).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
(frac{{BC}}{{sin A}} = frac{{AC}}{{sin B}} = frac{{AB}}{{sin C}}) ( Rightarrow AB = frac{{BC.sin C}}{{sin A}})
Mà: (BC = 5;(m);;;widehat C = {130^o};;widehat A = {10^o})
( Rightarrow AB = frac{{5.sin {{130}^o}}}{{sin {{10}^o}}} approx 22;(m))
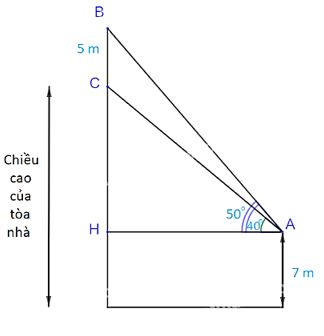
Xét tam giác ABH, vuông tại H ta có:
(sin widehat {BAH} = frac{{BH}}{{AB}})( Rightarrow BH = AB.,,sin widehat {BAH})
Mà: (AB approx 22;(m);;;widehat {BAH} = {50^o})
( Rightarrow BH approx 22.sin {50^o} approx 16,85;(m))
Vậy chiều cao của tòa nhà là: (BH-{rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{rm{ }}left( m right))
