Giải SGK Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác – CD – Sách Toán

Đề bài

Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, – \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.

Dựa vào các giá trị lượng giác để tính từng cạnh của tam giác MNP

Lời giải chi tiết

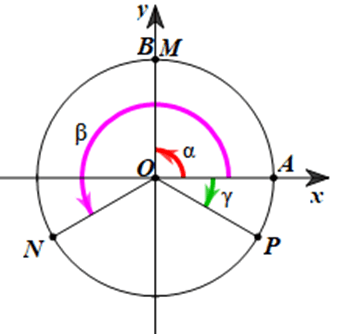
\(\begin{array}{l}(OM,ON) = (OA,ON) – (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} – {120^0} – {120^0} = {120^0}\end{array}\)

Cung MP = cung NP = cung NM

\(\Rightarrow MP = NP = NM\)

\(\Rightarrow \Delta MNP\) đều

Đề bài

Tính các giá trị lượng giác của mỗi góc sau: \(225^\circ ; – 225^\circ ; – 1035^\circ \);\(\frac{{5\pi }}{3};\frac{{19\pi }}{2}; – \frac{{159\pi }}{4}\)

Sử dụng các công thức biến đổi lượng giác sau:

Lời giải chi tiết

\(\begin{array}{l}\cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = – \cos \left( {{{45}^ \circ }} \right) = – \frac{{\sqrt 2 }}{2}\\\sin \left( {{{225}^ \circ }} \right) = \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = – \sin \left( {{{45}^ \circ }} \right) = – \frac{{\sqrt 2 }}{2}\\\tan \left( {225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = 1\\\cot \left( {225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = 1\end{array}\)

\(\begin{array}{l}\cos \left( { – {{225}^ \circ }} \right) = \cos \left( {{{225}^ \circ }} \right) = \cos \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = – \cos \left( {{{45}^ \circ }} \right) = – \frac{{\sqrt 2 }}{2}\\\sin \left( { – {{225}^ \circ }} \right) = – \sin \left( {{{225}^ \circ }} \right) = – \sin \left( {{{180}^ \circ } + {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { – 225^\circ } \right) = \frac{{\sin \left( {{{225}^ \circ }} \right)}}{{\cos \left( {{{225}^ \circ }} \right)}} = – 1\\\cot \left( { – 225^\circ } \right) = \frac{1}{{\tan \left( {225^\circ } \right)}} = – 1\end{array}\)

\(\begin{array}{l}\cos \left( { – {{1035}^ \circ }} \right) = \cos \left( {{{1035}^ \circ }} \right) = \cos \left( {{{6.360}^ \circ } – {{45}^ \circ }} \right) = \cos \left( { – {{45}^ \circ }} \right) = \cos \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { – {{1035}^ \circ }} \right) = – \sin \left( {{{1035}^ \circ }} \right) = – \sin \left( {{{6.360}^ \circ } – {{45}^ \circ }} \right) = – \sin \left( { – {{45}^ \circ }} \right) = \sin \left( {{{45}^ \circ }} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { – 1035^\circ } \right) = \frac{{\sin \left( { – {{1035}^ \circ }} \right)}}{{\cos \left( { – {{1035}^ \circ }} \right)}} = 1\\\cot \left( { – 1035^\circ } \right) = \frac{1}{{\tan \left( { – 1035^\circ } \right)}} = – 1\end{array}\)

\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{3}} \right) = \cos \left( {\pi + \frac{{2\pi }}{3}} \right) = – \cos \left( {\frac{{2\pi }}{3}} \right) = \frac{1}{2}\\\sin \left( {\frac{{5\pi }}{3}} \right) = \sin \left( {\pi + \frac{{2\pi }}{3}} \right) = – \sin \left( {\frac{{2\pi }}{3}} \right) = – \frac{{\sqrt 3 }}{2}\\\tan \left( {\frac{{5\pi }}{3}} \right) = \frac{{\sin \left( {\frac{{5\pi }}{3}} \right)}}{{\cos \left( {\frac{{5\pi }}{3}} \right)}} = – \sqrt 3 \\\cot \left( {\frac{{5\pi }}{3}} \right) = \frac{1}{{\tan \left( {\frac{{5\pi }}{3}} \right)}} = – \frac{{\sqrt 3 }}{3}\end{array}\)

\(\begin{array}{l}\cos \left( {\frac{{19\pi }}{2}} \right) = \cos \left( {8\pi + \frac{{3\pi }}{2}} \right) = \cos \left( {\frac{{3\pi }}{2}} \right) = \cos \left( {\pi + \frac{\pi }{2}} \right) = – \cos \left( {\frac{\pi }{2}} \right) = 0\\\sin \left( {\frac{{19\pi }}{2}} \right) = \sin \left( {8\pi + \frac{{3\pi }}{2}} \right) = \sin \left( {\frac{{3\pi }}{2}} \right) = \sin \left( {\pi + \frac{\pi }{2}} \right) = – \sin \left( {\frac{\pi }{2}} \right) = – 1\\\tan \left( {\frac{{19\pi }}{2}} \right)\\\cot \left( {\frac{{19\pi }}{2}} \right) = \frac{{\cos \left( {\frac{{19\pi }}{2}} \right)}}{{\sin \left( {\frac{{19\pi }}{2}} \right)}} = 0\end{array}\)

\(\begin{array}{l}\cos \left( { – \frac{{159\pi }}{4}} \right) = \cos \left( {\frac{{159\pi }}{4}} \right) = \cos \left( {40.\pi – \frac{\pi }{4}} \right) = \cos \left( { – \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( { – \frac{{159\pi }}{4}} \right) = – \sin \left( {\frac{{159\pi }}{4}} \right) = – \sin \left( {40.\pi – \frac{\pi }{4}} \right) = – \sin \left( { – \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( { – \frac{{159\pi }}{4}} \right) = \frac{{\cos \left( { – \frac{{159\pi }}{4}} \right)}}{{\sin \left( { – \frac{{159\pi }}{4}} \right)}} = 1\\\cot \left( { – \frac{{159\pi }}{4}} \right) = \frac{1}{{\tan \left( { – \frac{{159\pi }}{4}} \right)}} = 1\end{array}\)

Đề bài

Tính các giá trị lượng giác (nếu có) có mỗi góc sau:

a) \(\frac{\pi }{3} + k2\pi \,\,\left( {k \in Z} \right)\)

b) \(k\pi \,\,\left( {k \in Z} \right)\)

c) \(\frac{\pi }{2} + k\pi \,\,(k \in Z)\)

d) \(\frac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)

Giá trị lượng giác của các góc đặc biệt

Lời giải chi tiết

a)

\(\begin{array}{l}\cos \left( {\frac{\pi }{3} + k2\pi \,} \right) = \cos \left( {\frac{\pi }{3}} \right) = \frac{1}{2}\\\sin \left( {\frac{\pi }{3} + k2\pi \,} \right) = \sin \left( {\frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}\\\tan \left( {\frac{\pi }{3} + k2\pi \,} \right) = \frac{{\sin \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}}{{\cos \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}} = \sqrt 3 \\\cot \left( {\frac{\pi }{3} + k2\pi \,\,} \right) = \frac{1}{{\tan \left( {\frac{\pi }{3} + k2\pi \,\,} \right)}} = \frac{{\sqrt 3 }}{3}\end{array}\)

b)

\(\begin{array}{l}\cos \left( {k\pi \,} \right) = \left[ \begin{array}{l} – 1\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n + 1\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n\,\,\,\end{array} \right.\\\sin \left( {k\pi \,} \right) = 0\\\tan \left( {k\pi \,} \right) = \frac{{\sin \left( {k\pi \,\,} \right)}}{{\cos \left( {k\pi \,\,} \right)}} = 0\\\cot \left( {k\pi \,\,} \right)\end{array}\)

c)

\(\begin{array}{l}\cos \left( {\frac{\pi }{2} + k\pi \,} \right) = 0\\\sin \left( {\frac{\pi }{2} + k\pi \,} \right) = \left[ \begin{array}{l}\sin \left( { – \frac{\pi }{2}} \right)\, = – 1\,\,\,\,\,\,\,;k = 2n + 1\\\sin \left( {\frac{\pi }{2}\,} \right)\, = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;k = 2n\,\,\,\end{array} \right.\\\tan \left( {\frac{\pi }{2} + k\pi \,} \right)\\\cot \left( {\frac{\pi }{2} + k\pi \,\,} \right) = 0\end{array}\)

d)

Với k=2n+1 thì

\(\begin{array}{l}\cos \left( {\frac{\pi }{4} + k\pi \,} \right) = \cos \left( {\frac{\pi }{4} + (2n + 1)\pi \,} \right) = \cos \left( {\frac{\pi }{4} + 2n\pi + \pi \,} \right) = \cos \left( {\frac{\pi }{4} + \pi \,} \right) = – \cos \left( {\frac{\pi }{4}} \right) = – \frac{{\sqrt 2 }}{2}\\\sin \left( {\frac{\pi }{4} + k\pi \,} \right) = \sin \left( {\frac{\pi }{4} + (2n + 1)\pi \,} \right) = \sin \left( {\frac{\pi }{4} + 2n\pi + \pi \,} \right) = sin\left( {\frac{\pi }{4} + \pi \,} \right) = – \sin \left( {\frac{\pi }{4}} \right) = – \frac{{\sqrt 2 }}{2}\\\tan \left( {\frac{\pi }{4} + k\pi \,} \right) = 1\\\cot \left( {\frac{\pi }{4} + k\pi \,\,} \right) = 1\end{array}\)

Với k=2n thì

\(\begin{array}{l}\cos \left( {\frac{\pi }{4} + k\pi \,} \right) = co{\mathop{\rm s}\nolimits} \left( {\frac{\pi }{4} + 2n\pi \,} \right) = \cos \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\sin \left( {\frac{\pi }{4} + k\pi \,} \right) = \sin \left( {\frac{\pi }{4} + 2n\pi \,} \right) = \sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\\tan \left( {\frac{\pi }{4} + k\pi \,} \right) = 1\\\cot \left( {\frac{\pi }{4} + k\pi \,\,} \right) = 1\end{array}\)

Đề bài

Tính các giá trị lượng giác của góc \(\alpha \) trong mỗi trường hợp sau:

a) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\) với \(\frac{\pi }{2} < \alpha < \pi \)

b) \(\cos \alpha = – \frac{2}{3}\) với \( – \pi < \alpha < 0\)

c) \(\tan \alpha = 3\) với \( – \pi < \alpha < 0\)

d) \(\cot \alpha = – 2\) với \(0 < \alpha < \pi \)

Sử dụng các công thức sau :

\({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\, = \,1\)

\(\tan \alpha .\cot \alpha \,\,\, = \,\,\,1\) với \(\cos \alpha \ne 0;\sin \alpha \ne 0\)

\(1 + {\tan ^2}\alpha \,\,\, = \,\,\,\frac{1}{{{{\cos }^2}\alpha }}\) với \(\cos \alpha \ne 0\)

adsense

\(1 + {\cot ^2}\alpha \,\,\, = \,\,\,\frac{1}{{{{\sin }^2}\alpha }}\) với \(\sin \alpha \ne 0\)

Lời giải chi tiết

a) Ta có \({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\, = \,1\)

mà \(\sin \alpha = \frac{{\sqrt {15} }}{4}\) nên \({\cos ^2}\alpha + {\left( {\frac{{\sqrt {15} }}{4}} \right)^2}\,\,\, = \,1 \Rightarrow {\cos ^2}\alpha = \frac{1}{{16}}\)

Lại có \(\frac{\pi }{2} < \alpha < \pi \) nên \(\cos \alpha < 0 \Rightarrow \cos \alpha = – \frac{1}{4}\)

Khi đó \(\tan \alpha = \frac{{\sin \alpha }}{{co{\mathop{\rm s}\nolimits} \alpha }} = – \sqrt {15} ;\cot \alpha = \frac{1}{{\tan \alpha }} = – \frac{1}{{\sqrt {15} }}\)

b)

Ta có \({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\, = \,1\)

mà \(\cos \alpha = – \frac{2}{3}\) nên \({\sin ^2}\alpha + {\left( {\frac{{ – 2}}{3}} \right)^2}\,\,\, = \,1 \Rightarrow {\sin ^2}\alpha = \frac{5}{9}\)

Lại có \( – \pi < \alpha < 0\) nên \(\sin \alpha < 0 \Rightarrow \sin \alpha = – \frac{{\sqrt 5 }}{3}\)

Khi đó \(\tan \alpha = \frac{{\sin \alpha }}{{co{\mathop{\rm s}\nolimits} \alpha }} = \frac{{\sqrt 5 }}{2};\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{2}{{\sqrt 5 }}\)

c)

Ta có\(\tan \alpha = 3\) nên

\(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{3}\)

\(\frac{1}{{{{\cos }^2}\alpha }} = 1 + {\tan ^2}\alpha \,\,\, = \,1 + {3^2} = 10\,\, \Rightarrow {\cos ^2}\alpha = \frac{1}{{10}}\)

Mà \({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\, = \,1 \Rightarrow {\sin ^2}\alpha = \frac{9}{{10}}\)

Với \( – \pi < \alpha < 0\)thì \(\sin \alpha < 0 \Rightarrow \sin \alpha = – \sqrt {\frac{9}{{10}}} \)

Với \( – \pi < \alpha < – \frac{\pi }{2}\)thì \(\cos \alpha < 0 \Rightarrow \cos \alpha = – \sqrt {\frac{1}{{10}}} \)

và \( – \frac{\pi }{2} \le \alpha < 0\)thì \(\cos \alpha > 0 \Rightarrow \cos \alpha = \sqrt {\frac{1}{{10}}} \)

d)

Ta có\(\cot \alpha = – 2\) nên

\(\tan \alpha = \frac{1}{{\cot \alpha }} = – \frac{1}{2}\)

\(\frac{1}{{{{\sin }^2}\alpha }} = 1 + co{{\mathop{\rm t}\nolimits} ^2}\alpha \,\,\, = \,1 + {( – 2)^2} = 5\,\, \Rightarrow {\sin ^2}\alpha = \frac{1}{5}\)

Mà \({\cos ^2}\alpha + {\sin ^2}\alpha \,\,\, = \,1 \Rightarrow {\cos ^2}\alpha = \frac{4}{5}\)

Với \(0 < \alpha < \pi \)thì \(\sin \alpha > 0 \Rightarrow \sin \alpha = \sqrt {\frac{1}{5}} \)

Với \(0 < \alpha < \frac{\pi }{2}\)thì \(\cos \alpha > 0 \Rightarrow \cos \alpha = \sqrt {\frac{4}{5}} \)

và \(\frac{\pi }{2} \le \alpha < \pi \)thì \(\cos \alpha < 0 \Rightarrow \cos \alpha = – \sqrt {\frac{4}{5}} \)

Đề bài

Tính

a) \(A = {\sin ^2}5^\circ + {\sin ^2}10^\circ + {\sin ^2}15^\circ + … + {\sin ^2}85^\circ \) (17 số hạng)

b) \(B = \cos 5^\circ + \cos 10^\circ + \cos 15^\circ + … + \cos 175^\circ \) (35 số hạng)

Sử dụng công thức lượng giác sau:

\(\sin ({90^ \circ } – \alpha ) = \cos \alpha ;\,\,\cos ({180^ \circ } – \alpha ) = – \cos \alpha \)

Lời giải chi tiết

a)

\(A = {\sin ^2}5^\circ + {\sin ^2}10^\circ + {\sin ^2}15^\circ + … + {\sin ^2}85^\circ \\\,\,\,\,\,\, = \,({\sin ^2}5^\circ + {\sin ^2}85^\circ ) + ({\sin ^2}15^\circ + {\sin ^2}75^\circ ) + … + ({\sin ^2}35^\circ + {\sin ^2}55^\circ ) + {\sin ^2}45^\circ \\\,\,\,\,\,\, = \,({\sin ^2}5^\circ + {\cos ^2}5^\circ ) + ({\sin ^2}15^\circ + {\cos ^2}15^\circ ) + … + ({\sin ^2}35^\circ + {\cos ^2}35^\circ ) + {\sin ^2}45^\circ \\\,\,\,\,\,\, = 1 + 1 + … + 1 + \frac{1}{2} = \frac{{17}}{2}\)

b)

\(B = \cos 5^\circ + \cos 10^\circ + \cos 15^\circ + … + \cos 175^\circ \\\,\,\,\,\, = (\cos 5^\circ + \cos 175^\circ ) + (\cos 10^\circ + \cos 170^\circ ) + … + (\cos 85^\circ + \cos 95^\circ ) + \cos 90^\circ \\\,\,\,\,\, = 0 + 0 + …. + 0 + 0 = 0\)

Đề bài

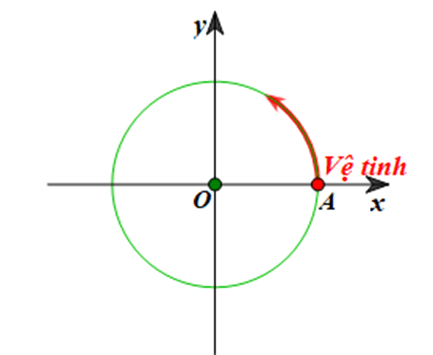
Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 3 giờ

a) Hãy tính quãng đường vệ tinh đã chuyển độ được sau: 1h; 3h; 5h

b) Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị?

Công thức tính chu vi hình tròn là \(2.R.\pi \) với R là bán kính đường tròn.

Lời giải chi tiết

a) Chiều dài một vòng của quỹ đạo là : \(9000.2.\pi \) (km)

Quãng đường vệ tinh đã chuyển động được sau 1 giờ là \(\frac{{9000.2.\pi }}{3} = 6000\pi \)(km)

Quãng đường vệ tinh đã chuyển động được sau 3 giờ là \(18000\pi \)(km)

Quãng đường vệ tinh đã chuyển động được sau 5 giờ là \(\frac{{9000.2.\pi }}{3}.5 = 30000\pi \)(km)

b)Vệ tinh chuyển động được quãng đường 200 000 km sau sô giờ là : \(\frac{{200000}}{{6000\pi }} \approx 11\)( giờ)