Giải SGK Bài 2: Giá trị lượng giác của một góc lượng giác – CTST – Sách Toán

Đề bài

Các đẳng thức sau có thể đồng thời xảy ra không?

a)    \(\sin \alpha  = \frac{3}{5}\) và \(\cos \alpha  =  – \frac{4}{5}\)

b)    \(\sin \alpha  = \frac{1}{3}\) và \(\cot \alpha  = \frac{1}{2}\)

c)    \(\tan \alpha  = 3\) và \(\cot \alpha  = \frac{1}{3}\)

Dựa vào công thức đã học để xác định

Lời giải chi tiết

a)    Ta có: \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \Leftrightarrow {\left( {\frac{3}{5}} \right)^2} + {\cos ^2}\alpha  = 1 \Leftrightarrow \cos \alpha  =  \pm \frac{4}{5}\)

Đẳng thức có thể đồng thời xảy ra

b)    Ta có: \(1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow 1 + {\cot ^2}\alpha  = \frac{1}{{{{\left( {\frac{1}{3}} \right)}^2}}} \Rightarrow \cot \alpha  =  \pm 2\sqrt 2 \)

Hai đẳng thức không thể đồng thời xảy ra

c)    Ta có: \(\tan \alpha .\cot \alpha  = 1 \Rightarrow 3.\cot \alpha  = 1 \Rightarrow \cot \alpha  = \frac{1}{3}\)

Đẳng thức có thể đồng thời xảy ra

Đề bài

Cho \(\sin \alpha  = \frac{{12}}{{13}}\) và \(\cos \alpha  =  – \frac{5}{{13}}\). Tính \(\sin \left( { – \frac{{15\pi }}{2} – \alpha } \right) – \cos \left( {13\pi  + \alpha } \right)\)

Dựa vào công thức lượng giác đặc biệt để tính

Lời giải chi tiết

Ta có:

\(\begin{array}{l}\sin \left( { – \frac{{15\pi }}{2} – \alpha } \right) – \cos \left( {13\pi  + \alpha } \right) =  – \sin \left( {\frac{{15\pi }}{2} + \alpha } \right) – \cos \left( {13\pi  + \alpha } \right) =  – \sin \left( {7\pi  + \frac{\pi }{2} – \alpha } \right) + \cos \alpha \\ = \sin \left( {\frac{\pi }{2} – \alpha } \right) + \cos \left( \alpha  \right) = 2\cos \left( \alpha  \right) = 2.\left( { – \frac{5}{{13}}} \right) = \frac{{ – 10}}{{13}}\end{array}\)

Đề bài

Tính các giá trị lượng giác của góc α, nếu:

a)    \(\sin \alpha  = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha  < \pi \)

b)    \(\cos \alpha  = \frac{2}{5}\) và \(0 < \alpha  < 90^\circ \)

c)    \(\tan \alpha  = \sqrt 3 \) và \(\pi  < \alpha  < \frac{{3\pi }}{2}\)

d)    \(\cot \alpha  = \frac{1}{2}\) và \(270^\circ  < \alpha  < 360^\circ \)

Dựa vào hệ thức cơ bản của hàm lượng giác để tính

Lời giải chi tiết

a)    Ta có: \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \Rightarrow {\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\alpha  = 1 \Rightarrow \cos \alpha  =  \pm \frac{{12}}{{13}}\)

Do \(\frac{\pi }{2} < \alpha  < \pi  \Rightarrow \cos \alpha  = \frac{-{12}}{{13}}\)\( \Rightarrow \left\{ \begin{array}{l}\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{-5}{{12}}\\\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{-{12}}{5}\end{array} \right.\)

b)    Ta có: \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \Rightarrow {\left( {\frac{2}{5}} \right)^2} + {\sin ^2}\alpha  = 1 \Rightarrow \sin \alpha  =  \pm \frac{{\sqrt {21} }}{5}\)

Do \(0 < \alpha  < 90^\circ  \Rightarrow \sin \alpha  = \frac{{\sqrt {21} }}{5}\)\( \Rightarrow \left\{ \begin{array}{l}\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\sqrt {21} }}{2}\\\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{2\sqrt {21} }}{{21}}\end{array} \right.\)

c)    Ta có: \(1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow 1 + {\left( {\sqrt 3 } \right)^2} = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow \cos \alpha  =  \pm \frac{1}{2}\)

Do \(\pi  < \alpha  < \frac{{3\pi }}{2} \Rightarrow \cos \alpha  = \frac{-1}{2}\) \( \Rightarrow \left\{ \begin{array}{l}\cot \alpha .\tan \alpha  = 1\\\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cot \alpha  = \frac{{\sqrt 3 }}{3}\\\sin \alpha  = \frac{{-\sqrt 3 }}{2}\end{array} \right.\)

d)    Ta có: \(1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow 1 + {\left( {\frac{1}{2}} \right)^2} = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow \sin \alpha  =  \pm \frac{{2\sqrt 5 }}{5}\)

Do \(270^\circ  < \alpha  < 360^\circ  \Rightarrow \sin \alpha  = \frac{{-2\sqrt 5 }}{5} \Rightarrow \left\{ \begin{array}{l}\cot \alpha .\tan \alpha  = 1\\\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\tan \alpha  = 2\\\cos \alpha  = \frac{{-\sqrt 5 }}{5}\end{array} \right.\)

Đề bài

Biểu diễn các giá trị lượng giác sau qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\) hoặc từ 0 đến \(45^\circ \) và tính

a)    \(\cos \frac{{21\pi }}{6}\)

b)    \(\sin \frac{{129\pi }}{4}\)

c)    \(\tan 1020^\circ \)

Dựa vào kiến thức vừa học được để tách các góc lượng giác

Lời giải chi tiết

adsense

a)    \(\cos \frac{{21\pi }}{6} = \cos \left( {3\pi  + \frac{\pi }{2}} \right) =  – \cos \left( {\frac{\pi }{2}} \right) = 0\)

b)    \(\sin \frac{{129\pi }}{4} = \sin \left( {32\pi  + \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\)

c)    \(\tan 1020^\circ  = \tan \left( {900^\circ  + 90^\circ  + 30^\circ } \right) = \tan \left( {90^\circ  + 30^\circ } \right) = \cot \left( {30^\circ } \right) = \sqrt 3 \)

Đề bài

Chứng minh các đẳng thức lượng giác sau:

a)    \({\sin ^4}\alpha  – {\cos ^4}\alpha  = 1 – 2{\cos ^2}\alpha \)

b)    \(\tan \alpha  + \cot \alpha  = \frac{1}{{\sin \alpha .\cos \alpha }}\)

Dựa vào các hệ thức cơ bản của lượng giác để chứng minh

Lời giải chi tiết

a)    Ta có:

\(\begin{array}{l}{\sin ^4}\alpha  – {\cos ^4}\alpha  = 1 – 2{\cos ^2}\alpha \\ \Leftrightarrow \left( {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha  – {{\cos }^2}\alpha } \right) = 1 – 2{\cos ^2}\alpha \\ \Leftrightarrow {\sin ^2}\alpha  – {\cos ^2}\alpha  – 1 + 2{\cos ^2}\alpha  = 0\\ \Leftrightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  – 1 = 0\\ \Leftrightarrow 1 – 1 = 0\\ \Leftrightarrow 0 = 0\end{array}\)

Đẳng thức luôn đúng

b)    Ta có:

\(\begin{array}{l}\tan \alpha  + \cot \alpha  = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{{{\sin }^2}\alpha  + {{\cos }^2}\alpha }}{{\cos \alpha .\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{1}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\end{array}\)

Đẳng thức luôn đúng

Đề bài

Rút gọn các biểu thức sau:

a)    \(\frac{1}{{\tan \alpha  + 1}} + \frac{1}{{\cot \alpha  + 1}}\)

b)    \(\cos \left( {\frac{\pi }{2} – \alpha } \right) – \sin \left( {\pi  + \alpha } \right)\)

c)    \(\sin \left( {\alpha  – \frac{\pi }{2}} \right) + \cos \left( { – \alpha  + 6\pi } \right) – \tan \left( {\alpha  + \pi } \right)\cot \left( {3\pi  – \alpha } \right)\)

Kết hợp giữa công thức cơ bản của lượng giác và hệ thức lượng giác để rút gọn

Lời giải chi tiết

a)

\(\begin{array}{l}\frac{1}{{\tan \alpha  + 1}} + \frac{1}{{\cot \alpha  + 1}} = \frac{{\cot \alpha  + 1 + \tan \alpha  + 1}}{{\left( {\tan \alpha  + 1} \right)\left( {\cot \alpha  + 1} \right)}}\\ = \frac{{\tan \alpha  + \cot \alpha  + 2}}{{\tan \alpha .\cot \alpha  + \tan \alpha  + \cot \alpha  + 1}} = \frac{{\tan \alpha  + \cot \alpha  + 2}}{{\tan \alpha  + \cot \alpha  + 2}} = 1\end{array}\)

b)    \(\cos \left( {\frac{\pi }{2} – \alpha } \right) – \sin \left( {\pi  + \alpha } \right) = \sin \alpha  + \sin \alpha  = 2\sin \alpha \)

c)    \(\begin{array}{l}\sin \left( {\alpha  – \frac{\pi }{2}} \right) + \cos \left( { – \alpha  + 6\pi } \right) – \tan \left( {\alpha  + \pi } \right)\cot \left( {3\pi  – \alpha } \right)\\ =  – \sin \left( {\frac{\pi }{2} – \alpha } \right) + \cos \left( \alpha  \right) – \tan \alpha .\cot \left( {\pi  – \alpha } \right)\\ =  – \cos \alpha  + \cos \alpha  + \tan \alpha .\cot \alpha \\ = 1\end{array}\)

Đề bài

Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được \(3\frac{1}{{10}}\) vòng là bao nhiêu, biết thanh độ dài OM là 15cm? Kết quả làm trong đến hàng phần mười.

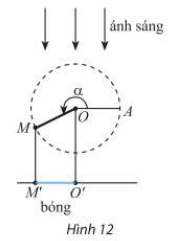
Dựa vào hàm lượng giác cơ bản để tính

Lời giải chi tiết

Thanh OM quay được \(3\frac{1}{{10}}\) \( \Rightarrow \alpha  = 3\frac{1}{{10}}.360^\circ  = 1116^\circ \)

Kẻ MH vuông góc Ox

Khi đó \(\begin{array}{l}M\left( {15.\cos 1116^\circ ;15.\sin 1116^\circ } \right)\\ \Rightarrow OH = \left| {\cos 1116^\circ } \right|.15 \approx 12,1\end{array}\)

Vậy độ dài bóng O’M’ của OM khi thanh quay được \(3\frac{1}{{10}}\) là 12,1cm

Đề bài

Khi xe đạp di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58cm? Giả sử độ dày của lốp xe không đáng kể. Kết quả làm trong đến hàng phần mười.

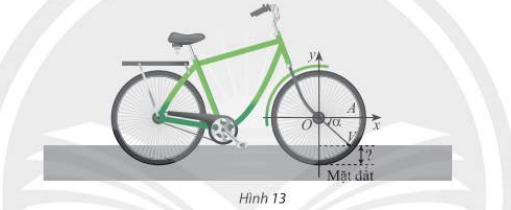
Dựa vào kiến thức đã học để làm

Lời giải chi tiết

Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha  = 11.60 = 660\left( {rad} \right)\)

Khi đó, tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left( {58.\cos \alpha ,58.\sin \alpha } \right) \approx \left( {56;15,2} \right)\)

Khi đó khoảng cách từ van đến mặt đất khoảng \(58 – 15,2 \approx 42,8\left( {cm} \right)\)