adsense
Giải SGK Bài 3. Các công thức lượng giác Toán 11 – CTST
Bài 1 trang 23 SGK Toán 11 tập 1 – CTST
Đề bài
Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:
a, \(\frac{{5\pi }}{{12}}\)
b, \(-{\rm{ }}{555^0}\)
Áp dụng công thức
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a – b} \right) = \sin a\cos b – \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b – \sin asinb\\\cos \left( {a – b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}}\\\tan \left( {a – b} \right) = \frac{{\tan a – \tan b}}{{1 + \tan a\tan b}}\end{array}\)
Lời giải chi tiết
a, Ta có:
\(\begin{array}{l}\cos \frac{{5\pi }}{{12}} = \cos \left( {\frac{\pi }{4} + \frac{\pi }{6}} \right) = \cos \frac{\pi }{4}\cos \frac{\pi }{6} – \sin \frac{\pi }{4}sin\frac{\pi }{6}\\ = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} – \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 – \sqrt 2 }}{4}\end{array}\)
\(\begin{array}{l}\sin \frac{{5\pi }}{{12}} = \sin \left( {\frac{\pi }{4} + \frac{\pi }{6}} \right) = \sin \frac{\pi }{4}\cos \frac{\pi }{6} + \cos \frac{\pi }{4}sin\frac{\pi }{6}\\ = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\end{array}\)
\(\tan \frac{{5\pi }}{{12}} = \frac{{sin\frac{{5\pi }}{{12}}}}{{cos\frac{{5\pi }}{{12}}}} = 2 – \sqrt 3 \)
\(\cot \frac{{5\pi }}{{12}} = \frac{1}{{\tan \frac{{5\pi }}{{12}}}} = \frac{1}{{2 – \sqrt 3 }}\)
b, Ta có:
\(\begin{array}{l}\cos \left( { – {{555}^0}} \right) = \cos \left( {3\pi + \frac{\pi }{{12}}} \right) = – \cos \frac{\pi }{{12}} = – \cos \left( {\frac{\pi }{3} – \frac{\pi }{4}} \right)\\ = – \left( {\cos \frac{\pi }{3}\cos \frac{\pi }{4} + \sin \frac{\pi }{3}sin\frac{\pi }{4}} \right) = – \frac{{\sqrt 6 + \sqrt 2 }}{4}\end{array}\)
\(\begin{array}{l}\sin \left( { – {{555}^0}} \right) = \sin \left( {3\pi + \frac{\pi }{{12}}} \right) = sin\frac{\pi }{{12}} = sin\left( {\frac{\pi }{3} – \frac{\pi }{4}} \right)\\ = \sin \frac{\pi }{3}\cos \frac{\pi }{4} – \cos \frac{\pi }{3}sin\frac{\pi }{4}\\ = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} – \frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 6 – \sqrt 2 }}{4}\end{array}\)
\(\tan \left( { – {{555}^0}} \right) = \frac{{\sin \left( { – {{555}^0}} \right)}}{{\cos \left( { – {{555}^0}} \right)}} = – 2 + \sqrt 3 \)
\(\cot \left( { – {{555}^0}} \right) = \frac{1}{{ – 2 + \sqrt 3 }} = – 2 – \sqrt 3 \)
Bài 2 trang 23 SGK Toán 11 tập 1 – CTST
Đề bài
Tính \(\sin \left( {\alpha + \frac{\pi }{6}} \right),\cos \left( {\frac{\pi }{4} – \alpha } \right)\) biết \(\sin \alpha = – \frac{5}{{13}},\pi < \alpha < \frac{{3\pi }}{2}\)
Áp dụng công thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\\cos \left( {a – b} \right) = \cos a\cos b + \sin asinb\end{array}\)
Lời giải chi tiết
\(\cos \alpha = – \sqrt {1 – {{\left( { – \frac{5}{{13}}} \right)}^2}} = – \frac{{12}}{{13}}\) (vì \(\pi < \alpha < \frac{{3\pi }}{2}\))
\(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \sin \alpha \cos \frac{\pi }{6} + \cos \alpha sin\frac{\pi }{6} = \frac{{ – 12 + 5\sqrt 3 }}{{26}}\)
\(\cos \left( {\frac{\pi }{4} – \alpha } \right) = \cos \frac{\pi }{4}\cos \alpha + \sin \frac{\pi }{4}sin\alpha = \frac{{ – 17\sqrt 2 }}{{26}}\)
Bài 3 trang 24 SGK Toán 11 tập 1 – CTST
Đề bài
Tính các giá trị lượng giác của góc 2\(\alpha \), biết:
a, \(\sin \alpha = \frac{{\sqrt 3 }}{3},0 < \alpha < \frac{\pi }{2}\)
b, \(\sin \frac{\alpha }{2} = \frac{3}{4},\pi < \alpha < 2\pi \)
Áp dụng công thức:
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a – {\sin ^2}a = 2{\cos ^2}a – 1 = 1 – 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 – {{\tan }^2}a}}\end{array}\)
Lời giải chi tiết
a, Ta có:
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\ \Rightarrow \cos \alpha = \pm \sqrt {1 – {{\sin }^2}\alpha } = \pm \sqrt {1 – {{\left( {\frac{{\sqrt 3 }}{3}} \right)}^2}} = \pm \frac{{\sqrt 6 }}{3}\end{array}\)
Vì \(0 < \alpha < \frac{\pi }{2} \Rightarrow \cos \alpha = \frac{{\sqrt 6 }}{3}\)
Khi đó:
\(\begin{array}{l}\sin 2\alpha = 2\sin \alpha .cos\alpha = 2.\frac{{\sqrt 3 }}{3}.\frac{{\sqrt 6 }}{3} = \frac{{2\sqrt 2 }}{3}\\cos2\alpha = 2{\cos ^2}\alpha – 1 = 2.{\left( {\frac{{\sqrt 6 }}{3}} \right)^2} – 1 = \frac{1}{3}\\\tan 2\alpha = \frac{{\sin 2\alpha }}{{cos2\alpha }} = \frac{{\frac{{2\sqrt 2 }}{3}}}{{\frac{1}{3}}} = 2\sqrt 2 \\\cot 2\alpha = \frac{1}{{\tan 2\alpha }} = \frac{1}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\end{array}\)
b,
Ta có:
\(\begin{array}{l}{\sin ^2}\frac{\alpha }{2} + {\cos ^2}\frac{\alpha }{2} = 1\\ \Rightarrow \cos \frac{\alpha }{2} = \pm \sqrt {1 – {{\sin }^2}\frac{\alpha }{2}} = \pm \sqrt {1 – {{\left( {\frac{3}{4}} \right)}^2}} = \pm \frac{{\sqrt 7 }}{4}\end{array}\)
Vì \(\pi < \alpha < 2\pi \Rightarrow \frac{\pi }{2} < \frac{\alpha }{2} < \pi \Rightarrow cos\alpha = – \frac{{\sqrt 7 }}{4}\)
Khi đó
\(\begin{array}{l}\sin \alpha = 2\sin \frac{\alpha }{2}.cos\frac{\alpha }{2} = 2.\frac{3}{4}.\left( { – \frac{{\sqrt 7 }}{4}} \right) = – \frac{{3\sqrt 7 }}{8}\\cos\alpha = 2{\cos ^2}\frac{\alpha }{2} – 1 = 2.{\left( { – \frac{{\sqrt 7 }}{4}} \right)^2} – 1 = – \frac{1}{8}\\\sin 2\alpha = 2\sin \alpha .cos\alpha = 2.\left( { – \frac{{3\sqrt 7 }}{8}} \right).\left( { – \frac{1}{8}} \right) = \frac{{3\sqrt 7 }}{{32}}\\cos2\alpha = 2{\cos ^2}\alpha – 1 = 2.{\left( { – \frac{1}{8}} \right)^2} – 1 = – \frac{{31}}{{32}}\\\tan 2\alpha = \frac{{\sin 2\alpha }}{{cos2\alpha }} = \frac{{\frac{{3\sqrt 7 }}{{32}}}}{{ – \frac{{31}}{{32}}}} = – \frac{{3\sqrt 7 }}{{31}}\\\cot 2\alpha = \frac{1}{{\tan 2\alpha }} = \frac{1}{{ – \frac{{3\sqrt 7 }}{{31}}}} = – \frac{{31\sqrt 7 }}{{21}}\end{array}\)
Bài 4 trang 24 SGK Toán 11 tập 1 – CTST
Đề bài
Rút gọn các biểu thức sau:
a, \(\sqrt 2 \sin \left( {\alpha + \frac{\pi }{4}} \right) – cos\alpha \),
b, \({\left( {cos\alpha + \sin \alpha } \right)^2} – \sin 2\alpha \)
Áp dụng công thức lượng giác
\(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\)
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
\(\sin 2a = 2\sin a\cos a\)
Lời giải chi tiết
a, Ta có:
\(\begin{array}{l}\sqrt 2 \sin \left( {\alpha + \frac{\pi }{4}} \right) – cos\alpha = \sqrt 2 .\left( {\sin \alpha \cos \frac{\pi }{4} + \cos \alpha \sin \frac{\pi }{4}} \right) – cos\alpha \\ = \sqrt 2 .\left( {\sin \alpha .\frac{{\sqrt 2 }}{2} + \cos \alpha .\frac{{\sqrt 2 }}{2}} \right) – cos\alpha \\ = \sin \alpha + \cos \alpha – cos\alpha \\ = \sin \alpha \end{array}\)
b, Ta có:
\(\begin{array}{l}{\left( {cos\alpha + \sin \alpha } \right)^2} – \sin 2\alpha \\ = co{s^2}\alpha + {\sin ^2}\alpha + 2cos\alpha \sin \alpha – 2\sin \alpha cos\alpha \\ = 1\end{array}\)
Bài 5 trang 24 SGK Toán 11 tập 1 – CTST
Đề bài
Tính các giá trị lượng giác của góc \(\alpha \), biết:
a, \(cos2\alpha = \frac{2}{5}, – \frac{\pi }{2} < \alpha < 0\)
b, \(\sin 2\alpha = – \frac{4}{9},\frac{\pi }{2} < \alpha < \frac{{3\pi }}{4}\)
Sử dụng các công thức lượng giác để tính toán
Lời giải chi tiết
a, Ta có:
\(\begin{array}{l}cos2\alpha = 2{\cos ^2}\alpha – 1 = \frac{2}{5}\\ \Leftrightarrow {\cos ^2}\alpha = \frac{7}{{10}} \Rightarrow \cos \alpha = \pm \frac{{\sqrt {70} }}{{10}}\end{array}\)
Vì \( – \frac{\pi }{2} < \alpha < 0 \Rightarrow \cos \alpha = \frac{{\sqrt {70} }}{{10}}\)
Lại có:
adsense
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\ \Rightarrow {\sin ^2}\alpha = 1 – \frac{7}{{10}} = \frac{3}{{10}}\\ \Rightarrow \sin \alpha = \pm \frac{{\sqrt {30} }}{{100}}\end{array}\)
\( – \frac{\pi }{2} < \alpha < 0 \Rightarrow \sin \alpha = – \frac{{\sqrt {30} }}{{100}}\)
\(\begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{cos\alpha }} = \frac{{ – \frac{{\sqrt {30} }}{{100}}}}{{\frac{{\sqrt {70} }}{{10}}}} = – \frac{{\sqrt 3 }}{{\sqrt 7 }}\\\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{ – \frac{{\sqrt 3 }}{{\sqrt 7 }}}} = – \frac{{\sqrt 7 }}{{\sqrt 3 }}\end{array}\)
b, Ta có:
\(\begin{array}{l}{\sin ^2}2\alpha + {\cos ^2}2\alpha = 1\\ \Rightarrow \cos 2\alpha = \sqrt {1 – {{\left( { – \frac{4}{9}} \right)}^2}} = \pm \frac{{\sqrt {65} }}{9}\end{array}\)
Vì \(\frac{\pi }{2} < \alpha < \frac{{3\pi }}{4} \Rightarrow \pi < 2\alpha < \frac{{3\pi }}{2} \Rightarrow cos2\alpha = – \frac{{\sqrt {65} }}{9}\)
\(\begin{array}{l}cos2\alpha = 2{\cos ^2}\alpha – 1 = – \frac{{\sqrt {65} }}{9}\\ \Leftrightarrow {\cos ^2}\alpha = \frac{{9 – \sqrt {65} }}{{18}} \Rightarrow \cos \alpha = \pm \sqrt {\frac{{9 – \sqrt {65} }}{{18}}} \end{array}\)
Vì \(\frac{\pi }{2} < \alpha < \frac{{3\pi }}{4} \Rightarrow \cos \alpha = – \sqrt {\frac{{9 – \sqrt {65} }}{{18}}} \)
Lại có:
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\ \Rightarrow {\sin ^2}\alpha = 1 – \frac{{9 – \sqrt {65} }}{{18}} = \frac{{9 + \sqrt {65} }}{{18}}\\ \Rightarrow \sin \alpha = \pm \sqrt {\frac{{9 + \sqrt {65} }}{{18}}} \end{array}\)
Vì Vì \(\frac{\pi }{2} < \alpha < \frac{{3\pi }}{4} \Rightarrow \sin \alpha = \sqrt {\frac{{9 + \sqrt {65} }}{{18}}} \)
\(\begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{cos\alpha }} = \frac{{\sqrt {\frac{{9 + \sqrt {65} }}{{18}}} }}{{ – \sqrt {\frac{{9 – \sqrt {65} }}{{18}}} }} \approx – 4,266\\\cot \alpha = \frac{1}{{\tan \alpha }} \approx – 0,234\end{array}\)
Bài 6 trang 24 SGK Toán 11 tập 1 – CTST
Đề bài
Chứng minh rằng tam giác ABC, ta có \(\sin A = \sin B.\cos C + \sin C.\cos B\)
Sử dụng định lý tổng 3 góc trong một tam giác bằng 1800 và áp dụng công thức cộng.
Lời giải chi tiết
Ta có: \(A + B + C = {180^0}\)(tổng 3 góc trong một tam giác)
\(\begin{array}{l} \Rightarrow A = {180^0} – \left( {B + C} \right)\\ \Leftrightarrow \sin A = \sin \left( {{{180}^0} – \left( {B + C} \right)} \right)\\ \Leftrightarrow \sin A = \sin \left( {B + C} \right) = \sin B.\cos C + \sin C.\cos B\end{array}\)
Bài 7 trang 24 SGK Toán 11 tập 1 – CTST
Đề bài
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn \(\widehat {CAD} = {30^0}\). Tính \(\tan \widehat {BAD}\), từ đó tính độ dài cạnh CD.
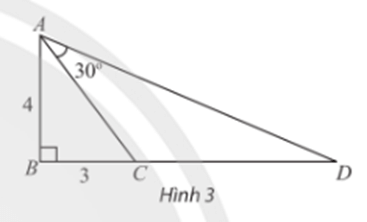
Nhìn hình vẽ để tính \(\tan \widehat {BAC}\), sau đó áp dụng công thức cộng để tính \(\tan \widehat {BAD}\).
Lời giải chi tiết
Xét tam giác ABC vuông tại B có:
\(\tan \widehat {BAC} = \frac{3}{4}\)
Suy ra, \(\tan \widehat {BAD} = \tan \left( {\widehat {BAC} + \widehat {CAD}} \right) = \tan \left( {\widehat {BAC} + {{30}^0}} \right)\)
\( = \frac{{\tan \widehat {BAC} + \tan {{30}^0}}}{{1 – \tan \widehat {BAC}.\tan {{30}^0}}} = \frac{{\frac{3}{4} + \frac{{\sqrt 3 }}{3}}}{{1 – \frac{3}{4}.\frac{{\sqrt 3 }}{3}}} \approx 2,34\)
Xét tam giác vuông ABD vuông tại B có:
\(\begin{array}{l}BD = AB.\tan \widehat {BAD} = 4.2,34 \approx 9,36\\ \Rightarrow CD = BD – BC \approx 9,36 – 3 \approx 6,36\end{array}\)
Bài 8 trang 24 SGK Toán 11 tập 1 – CTST
Đề bài
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho \(\alpha \) là góc quay của trục khuỷu, O là vị trí của pít – tông khi \(\alpha = \frac{\pi }{2}\) và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.
a) Biết IA = 8cm, viết công thức tính tọa độ \({x_M}\)của điểm M trên trục Ox theo \(\alpha \).
b) Ban đầu \(\alpha = 0\). Sau 1 phút chuyển động, \({x_M}\)= – 3cm. Xác định\({x_M}\) sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười
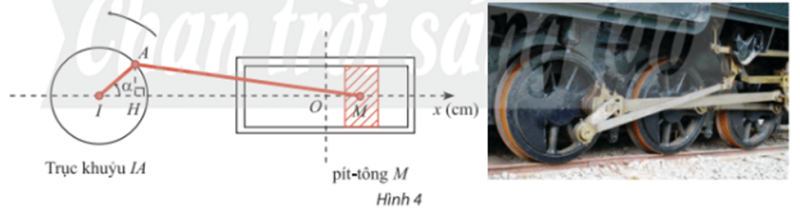
Lời giải chi tiết
a, Tại \(\alpha = \frac{\pi }{2}\) thì H trùng I, M trùng O nên MH = OI do đó OM = IH.
Xét tam giác AHI vuông tại H có: \(IH = cos\alpha .IA = 8cos\alpha .\)
\( \Rightarrow {x_M} = OM = IH = 8cos\alpha \)
b, Sau khi chuyển động được 1 phút, trục khuỷu quay được một góc là \(\alpha \)
Khi đó \({x_M} = – 3cm \Rightarrow cos\alpha = – \frac{3}{8}\)
Sau khi chuyển động 2 phút, trục khuỷu quay được một góc \(2\alpha \), nên:
\({x_M} = 8cos2\alpha = 8\left( {2{{\cos }^2}\alpha – 1} \right)\)\( = 8\left( {2{{\left( { – \frac{3}{8}} \right)}^2} – 1} \right) \approx – 5,8 cm\)
Bài 9 trang 24 SGK Toán 11 tập 1 – CTST
Đề bài
Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là \(\frac{{2\pi }}{3}\) và số đo góc (OA, OM) là \(\alpha \).
a) Tính sin\(\alpha \) và cos \(\alpha \).
b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Dựa vào hình vẽ để tìm sin\(\alpha \)và cos \(\alpha \); sử dụng công thức cộng để tính sin của các góc lượng giác (OA, ON) và (OA, OP).
Lời giải chi tiết
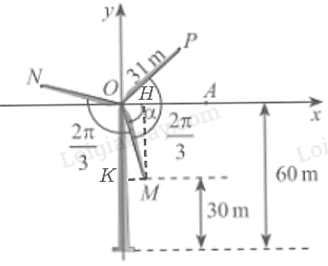
a, Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy.
Ta có: MH = 60 – 30 = 30 m.
Khi đó hoành độ điểm M là 30.
⇒ \(\;\sin \alpha {\rm{ }} = \;\frac{{MH}}{{OM}} = \;\frac{{30}}{{31}}\)
\( \Rightarrow \cos \alpha = \sqrt {1 – {{\left( {\frac{{30}}{{31}}} \right)}^2}} = \frac{{\sqrt {61} }}{{31}}\)
b, Vì các cánh quạt tạo thành 3 góc bằng nhau nên \(\widehat {MOP} = \widehat {NOP} = \widehat {MON} = {120^0}\)
\( \Rightarrow \widehat {AOP} = \widehat {MOP} – \widehat {MOA}\)
\( \Leftrightarrow \sin \widehat {AOP} = \sin \left( {\widehat {MOP} – \widehat {MOA}} \right) = \sin \widehat {MOP}.\cos \widehat {MOA} – \cos \widehat {MOP}.\sin \widehat {MOA}\)
\( = \sin \frac{{2\pi }}{3}.\cos \alpha – \cos \frac{{2\pi }}{3}.\sin \alpha \approx 0,7\)
Vì vậy chiều cao của điểm P so với mặt đất là:
31. \(\sin \widehat {AOP}\) + 60 = 31.0,7+ 60 \( \approx \) 81,76 m.
Ta có:
\(\cos \widehat {AOP} \approx \sqrt {1 – 0,{7^2}} = 0,71\)
\(\widehat {AON} = \widehat {AOP} + \widehat {PON}\)
\(\begin{array}{l} \Leftrightarrow \sin \widehat {AON} = \sin \left( {\widehat {AOP} + \widehat {PON}} \right)\\ \Leftrightarrow \sin \widehat {AON} = \sin \widehat {AOP}.\cos \widehat {PON} + \cos \widehat {AOP}.\sin \widehat {PON}\\ \Leftrightarrow \sin \widehat {AON} = 0,7.\cos \frac{{2\pi }}{3} + 0,71.\sin \frac{{2\pi }}{3} \approx 0,26\end{array}\)
\( \Rightarrow \sin \left( {OA,ON} \right) = \sin \widehat {AON} \approx 0,26\)
Vì vậy chiều cao của điểm N so với mặt đất là:
31. \(\sin \widehat {AON}\) + 60 = 31.0,26+ 60\( \approx \) 68,2 m.
