adsense
Giải SGK Bài 3. Hàm số lượng giác và đồ thị – Toán 11 CD
================
Bài 1 trang 31 SGK Toán 11 tập 1 – CD
Đề bài
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn \(\left[ { – 2\pi ;2\pi } \right]\) để:
a) Hàm số y = sinx nhận giá trị bằng 1
b) Hàm số y = sinx nhận giá trị bằng 0
c) Hàm số y = cosx nhận giá trị bằng – 1
d) Hàm số y = cosx nhận giá trị bằng 0
Sử dụng đồ thị hàm số.
Lời giải chi tiết
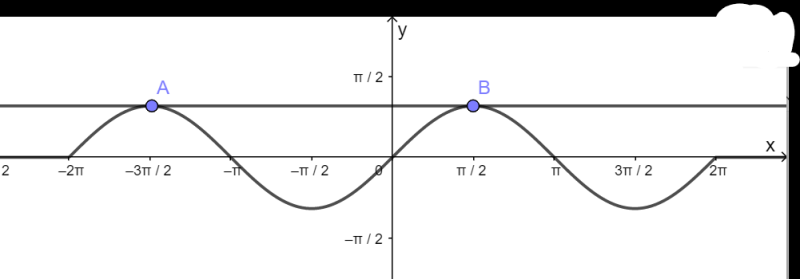
a) Hàm số y = sinx nhận giá trị bằng 1
– Vẽ hàm số y = sinx trên đoạn \(\left[ { – 2\pi ;2\pi } \right]\)
– Vẽ hàm số y = 1
– Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,…
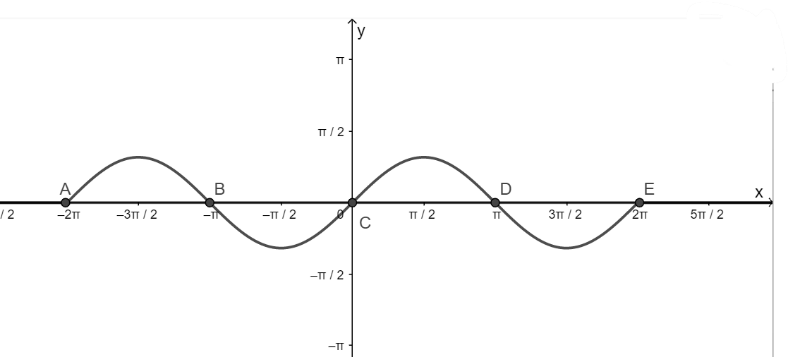
b) Hàm số y = sinx nhận giá trị bằng 0
– Vẽ hàm số y = sinx trên đoạn \(\left[ { – 2\pi ;2\pi } \right]\)
– Vẽ hàm số y = 0
– Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,…
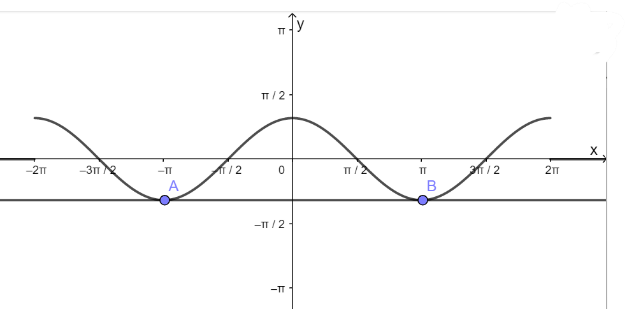
c) Hàm số y = cosx nhận giá trị bằng – 1
– Vẽ hàm số y = cosx trên đoạn \(\left[ { – 2\pi ;2\pi } \right]\)
– Vẽ hàm số y = – 1
– Lấy giao điểm của hai hàm số y = cosx và y = – 1 là A, B,…
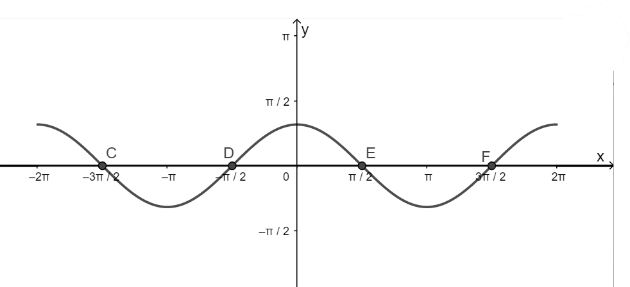
d) Hàm số y = cosx nhận giá trị bằng 0
– Vẽ hàm số y = cosx trên đoạn \(\left[ { – 2\pi ;2\pi } \right]\)
– Vẽ hàm số y = 0
– Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,…
Bài 2 trang 31 SGK Toán 11 tập 1 – CD
Đề bài
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { – \pi ;\frac{{3\pi }}{2}} \right)\) để:
a) Hàm số y = tanx nhận giá trị bằng – 1
b) Hàm số y = tanx nhận giá trị bằng 0
c) Hàm số y = cotx nhận giá trị bằng 1
d) Hàm số y = cotx nhận giá trị bằng 0
Sử dụng đồ thị hàm số.
Lời giải chi tiết
a) Hàm số y = tanx nhận giá trị bằng – 1
– Vẽ hàm số y = tanx trên khoảng \(\left( { – \pi ;\frac{{3\pi }}{2}} \right)\)
– Vẽ hàm số y = – 1
– Lấy giao điểm của hai hàm số y = tanx và y = – 1
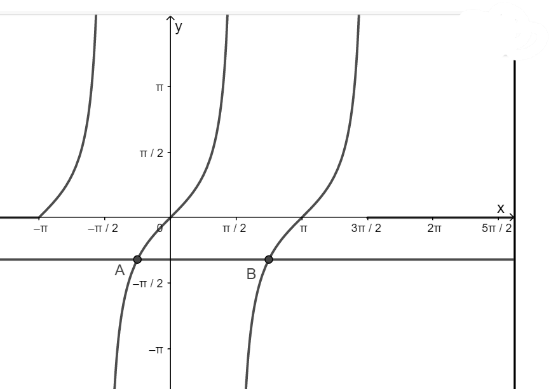
b) Hàm số y = tanx nhận giá trị bằng 0
– Vẽ hàm số y = tanx trên khoảng \(\left( { – \pi ;\frac{{3\pi }}{2}} \right)\)
– Vẽ hàm số y = 0
– Lấy giao điểm của hai hàm số y = tanx và y = 0
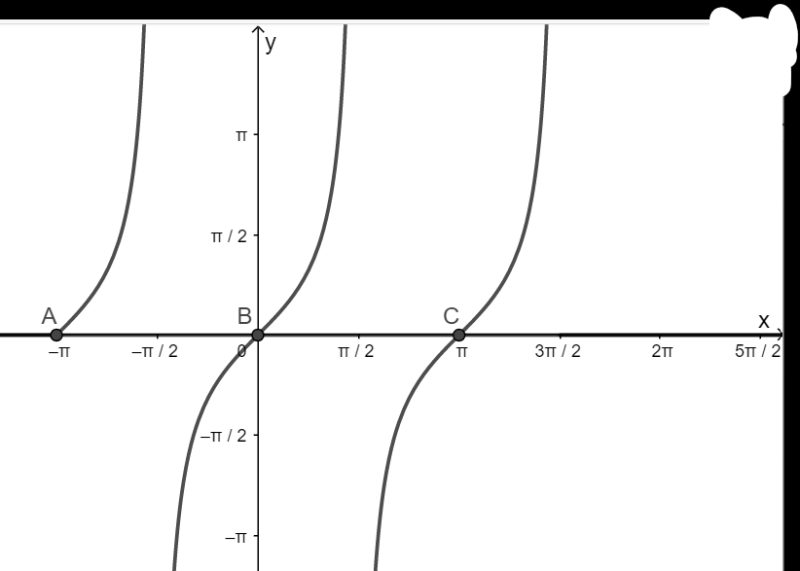
c) Hàm số y = cotx nhận giá trị bằng 1
– Vẽ hàm số y = cotx trên khoảng \(\left( { – \pi ;\frac{{3\pi }}{2}} \right)\)
– Vẽ hàm số y = 1
– Lấy giao điểm của hai hàm số y = cotx và y = 1
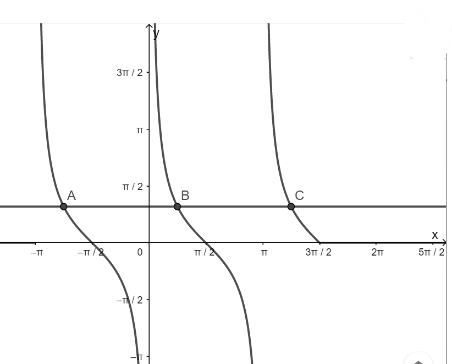
d) Hàm số y = cotx nhận giá trị bằng 0
– Vẽ hàm số y = cotx trên khoảng \(\left( { – \pi ;\frac{{3\pi }}{2}} \right)\)
– Vẽ hàm số y = 0
– Lấy giao điểm của hai hàm số y = tanx và y = 0
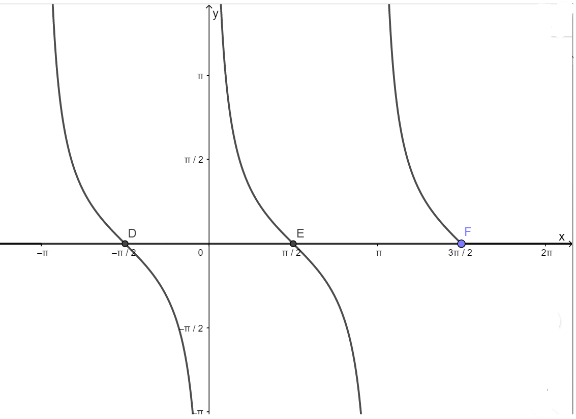
Bài 3 trang 31 SGK Toán 11 tập 1 – CD
Đề bài
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { – \frac{{9\pi }}{2}; – \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { – 20\pi ; – 19\pi } \right),\left( { – 9\pi ; – 8\pi } \right)\)
Sử dụng khoản biến thiên của hàm số sin x, cos x.
Lời giải chi tiết
a) y = sinx
– Khoảng \(\left( { – \frac{{9\pi }}{2}; – \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
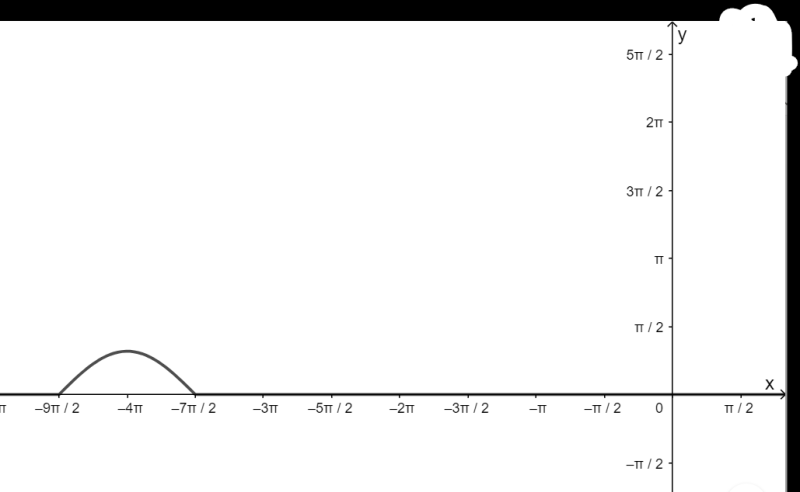
+ Đồng biến trên khoảng \(\left( { – \frac{{9\pi }}{2}; – 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { – 4\pi ; – \frac{{7\pi }}{2}} \right)\)
– Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
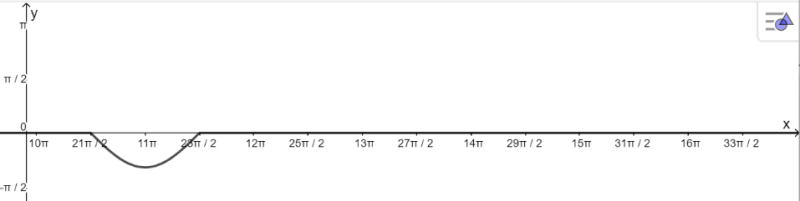
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
adsense
Bài 4 trang 31 SGK Toán 11 tập 1 – CD
Đề bài
Dùng đồ thị hàm số, hãy cho biết:
a) Với mỗi \(m \in \left[ { – 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Với mỗi \(m \in \left[ { – 1;1} \right]\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Với mỗi \(m \in \mathbb{R}\), có bao nhiêu giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)
Sử dụng đồ thị của hàm số sin , cos , tan , cot
Lời giải chi tiết
a) Đồ thị hàm số:
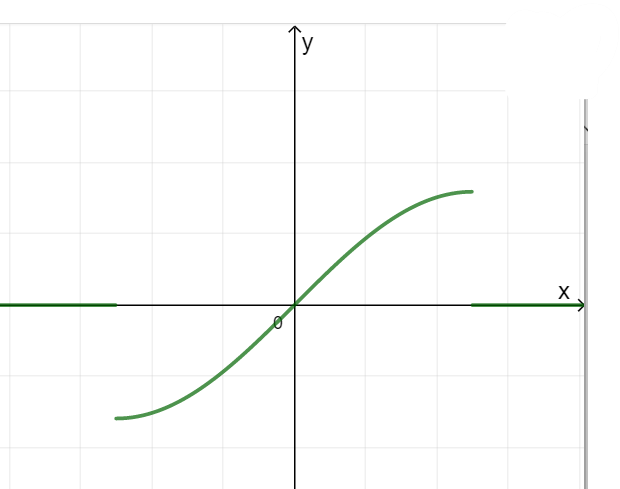
– Với mỗi \(m \in \left[ { – 1;1} \right]\) chỉ có 1 giá trị \(\alpha \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
b) Đồ thị hàm số:
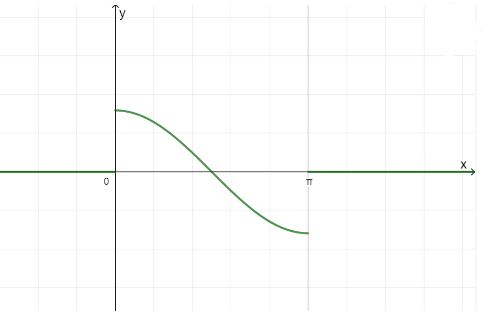
– Với mỗi \(m \in \left[ { – 1;1} \right]\) có 1 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
c) Đồ thị hàm số:
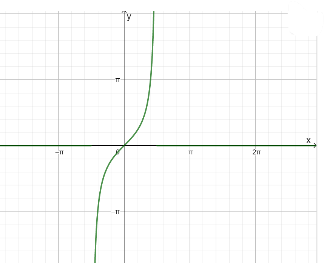
– Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\tan \alpha = m\)
d) Đồ thị hàm số:
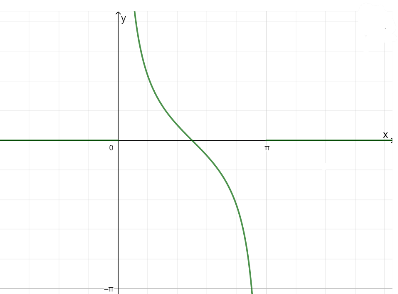
– Với mỗi \(m \in \mathbb{R}\), có 2 giá trị \(\alpha \in \left[ {0;\pi } \right]\) sao cho \(\cot \alpha = m\)
Bài 5 trang 31 SGK Toán 11 tập 1 – CD
Đề bài
Xét tính chẵn, lẻ của các hàm số:
a) \(y = \sin x\cos x\)
b) \(y = \tan x + \cot x\)
c) \(y = {\sin ^2}x\)
Dựa vào tính chẵn, lẻ của hàm số.
Lời giải chi tiết
a) Ta có:
\(\left. \begin{array}{l}f\left( { – x} \right) = \sin \left( { – x} \right).\cos \left( { – x} \right) = – \sin x.\cos x\\f\left( x \right) = \sin x.\cos x\end{array} \right\} \Rightarrow f\left( { – x} \right) = – f\left( x \right)\)
ð Hàm số \(y = \sin x\cos x\) là hàm số lẻ
b) Ta có:
\(\left. \begin{array}{l}f\left( { – x} \right) = \tan \left( { – x} \right) + \cot \left( { – x} \right) = – \tan x – \cot x\\f\left( x \right) = \tan x + \cot x\end{array} \right\} \Rightarrow f\left( { – x} \right) = – f\left( x \right)\)
ð Hàm số \(y = \tan x + \cot x\) là hàm số lẻ
c) Ta có:
\(\left. \begin{array}{l}f\left( { – x} \right) = {\sin ^2}\left( { – x} \right) = {\left( { – \sin \left( x \right)} \right)^2} = {\sin ^2}x\\f\left( x \right) = {\sin ^2}x\end{array} \right\} \Rightarrow f\left( { – x} \right) = f\left( x \right)\)
ð Hàm số \(y = {\sin ^2}x\) là hàm số chẵn
Bài 6 trang 31 SGK Toán 11 tập 1 – CD
Đề bài
Một dao động điều hòa có phương trình li độ dao động là: \(x = A\cos \left( {\omega t + \varphi } \right)\), trong đó t là thời gian tính bằng giây, A là biên độ dao động và x là li độ dao động đều được tính bằng centimet. Khi đó, chu kì T của dao động là \(T = \frac{{2\pi }}{\omega }\). Xác định giá trị của li độ khi \(t = 0,t = \frac{T}{4},t = \frac{T}{2},t = \frac{{3T}}{4},t = T\) và vẽ đồ thị biểu diễn li độ của dao động điều hòa trên đoạn \(\left[ {0;2T} \right]\) trong trường hợp:
a) \(A = 3cm,\varphi = 0\)
b) \(A = 3cm,\varphi = – \frac{\pi }{2}\)
c) \(A = 3cm,\varphi = \frac{\pi }{2}\)
Thay các giá trị vào phương trình li độ để tính
Lời giải chi tiết
Ta có
\(\begin{array}{l}t = 0 \Rightarrow \omega t = 0\\t = \frac{T}{4} \Rightarrow \omega t = \omega .\frac{{\frac{{2\pi }}{\omega }}}{4} = \frac{\pi }{2}\\t = \frac{T}{2} \Rightarrow \omega t = \omega .\frac{{\frac{{2\pi }}{\omega }}}{2} = \pi \\t = \frac{{3T}}{4} \Rightarrow \omega t = \omega .\frac{{3.\frac{{2\pi }}{\omega }}}{4} = \frac{{3\pi }}{2}\\t = T \Rightarrow \omega t = \omega .\frac{{2\pi }}{\omega } = 2\pi \end{array}\)
a) \(A = 3cm,\varphi = 0\)
+) Với t=0 thì \(x = 3\cos \left( {\omega .0 + 0} \right) = 3\)
+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} + 0} \right) = 0\)
+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi + 0} \right) = – 3\)
+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + 0} \right) = 0\)
+Với \(t = T\)thì \(x = 3\cos \left( {2\pi + 0} \right) = 3\)
b) \(A = 3cm,\varphi = – \frac{\pi }{2}\)
+) Với t=0 thì \(x = 3\cos \left( {0 – \frac{\pi }{2}} \right) = 0\)
+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} – \frac{\pi }{2}} \right) = 3\)
+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi – \frac{\pi }{2}} \right) = 0\)
+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} – \frac{\pi }{2}} \right) = 3\)
+Với \(t = T\)thì \(x = 3\cos \left( {2\pi – \frac{\pi }{2}} \right) = 0\)
c) \(A = 3cm,\varphi = \frac{\pi }{2}\)
+) Với t=0 thì \(x = 3\cos \left( {0 + \frac{\pi }{2}} \right) = 0\)
+) Với \(t = \frac{T}{4}\)thì \(x = 3\cos \left( {\frac{\pi }{2} + \frac{\pi }{2}} \right) = 3\)
+) Với \(t = \frac{T}{2}\)thì \(x = 3\cos \left( {\pi + \frac{\pi }{2}} \right) = 0\)
+)Với \(t = \frac{{3T}}{4}\)thì \(x = 3\cos \left( {\frac{{3\pi }}{2} + \frac{\pi }{2}} \right) = 3\)
+Với \(t = T\)thì \(x = 3\cos \left( {2\pi + \frac{\pi }{2}} \right) = 0\)
Bài 7 trang 31 SGK Toán 11 tập 1 – CD
Đề bài
Trong bài toán mở đầu, hãy chỉ ra một số giá trị của x để ông đựng nước cách mặt nước 2m.
Sử dụng các công thức liên quan tới hàm số sin
Lời giải chi tiết
Để ông đựng nước cách mặt nước 2m thì \(h = \left| y \right| = 2\)
Hay \(\left| {2,5.\sin \left( {2\pi x – \frac{\pi }{2}} \right) + 2} \right| = 2\)
Suy ra \(2,5.\sin \left( {2\pi x – \frac{\pi }{2}} \right) + 2 = 2\) hoặc \(2,5.\sin \left( {2\pi x – \frac{\pi }{2}} \right) + 2 = – 2\)
*) \(2,5.\sin \left( {2\pi x – \frac{\pi }{2}} \right) + 2 = 2\\ \Leftrightarrow \sin \left( {2\pi x – \frac{\pi }{2}} \right) = 0\\ \Leftrightarrow 2\pi x – \frac{\pi }{2} = k\pi ,k \in Z\\ \Leftrightarrow 2x – \frac{1}{2} = k,k \in Z\\ \Leftrightarrow x = \frac{{2k + 1}}{4},k \in Z\\ \Leftrightarrow x \in \left\{ {….; – \frac{1}{4};\frac{1}{4};\frac{3}{4};….} \right\}\)
*)\(2,5.\sin \left( {2\pi x – \frac{\pi }{2}} \right) + 2 = – 2\\ \Leftrightarrow \sin \left( {2\pi x – \frac{\pi }{2}} \right) = – 1,6\, < – 1\)
Vì tập giá trị của hàm số sin là \(\left[ { – 1;1} \right]\) nên trong trường hợp này phương trình vô nghiệm.
